Нахождение корня в Mathcad
Лабораторная работа №1
Решение нелинейных уравнений
Вариант №7
Задание:
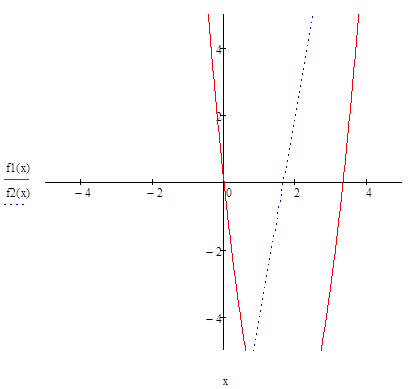
1. Построить график функции f(x).Отделить все корни, лежащие на данном отрезке.
2. Вычислить наибольший из корней методами, указанными в варианте. Точность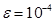 
. Программа должна быть универсальной. Методы оформить в виде отдельных подпрограмм, содержащих проверку условий сходимости метода. Метод, начальное приближение 
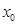задавать как параметр, вводимый с клавиатуры. Вычислить корень при различных значениях 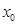. Вывод на консоль: метод, 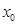, номер итерации - k, 
, 
.
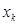3. Сравнить число необходимых итераций в обоих методах, указать преимущества и недостатки методов. Сделать выводы.
4. Графически проиллюстрировать сходимость методов для своего уравнения.
5. Вычислить наибольший из корней в MathCAD.
Ход работы
 |
 |
 |
 |
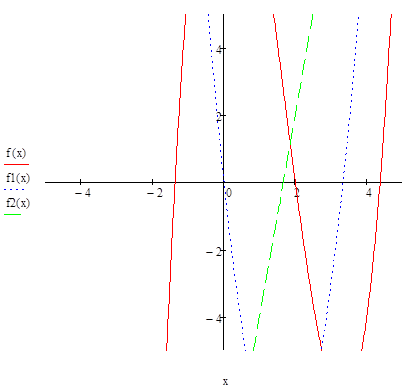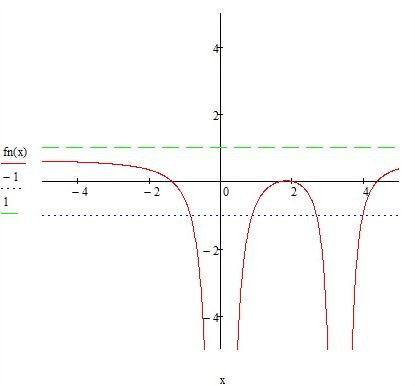
Из графика видно, что первый корень находится на отрезке [-2;-1], второй на отрезке [1;3], а третий- [3;5]. Наибольший корень лежит на отрезке [3;5].
Составим программу для вычисления наибольшего из корней данного уравнения:
Текст программы:
#include <stdio.h>
#include <math.h>
#include<conio.h>
double a,b;
int metod;
int i;
double k,fn,f1,f2,x,xn,xk,fn2;
void newton(double a,double b)
{
int i;
x=b;
k=1;
printf("Xo=%f\n", x);
for (i=1; k>=0.0001; i++)
{
fn=pow(x,3)-5*x*x+12;
f1=3*x*x-10*x;
f2=6*x-10;
xn=x-(fn/f1);//формула итераций
k=abs(x-xn);
if(k>0.0001)
{x=xn;}
printf ("k=%d Xk=%.10f Ek=%.10f \n",i,xn,k);
if (i>30)
{
printf ("----------ERROR------------\n");
printf ("RESTRICTION OF NUMBER OF ITERATIONS\n"); //ОГРАНИЧЕНИЕ ЧИСЛА ИТЕРАЦИЙ
break;
}
printf ("x*=%.10f\n", xn);
}
}
void vegstein(double a,double b)
{
int i;
x=b;
printf("Xo=%f\n", x);
k=1;
fn= pow(x,3)-5*x*x+12;
f1=3*x*x-10*x;
f2=6*x-10;
fn2= pow(xn,3)-5*xn*xn+12;
xn=x-(fn/f1);//формула итераций
printf("X1=%f\n", xn);
k=x-xn;
if (k<0)
{
k*=-1;
}
for (i=1; k>= 0.0001; i++)
{
fn= pow(x,3)-5*x*x+12;
f1=3*x*x-10*x;
f2=6*x-10;
fn2= pow(xn,3)-5*xn*xn+12;
if (i>30)
{
printf ("----------ERROR------------\n");
printf ("RESTRICTION OF NUMBER OF ITERATIONS\n"); //ОГРАНИЧЕНИЕ ЧИСЛА ИТЕРАЦИЙ
break;
}
xk=xn-(fn2*(xn-x)/(fn2-fn));//формула итераций
k=xk-xn;
if (k<0)
{
k*=-1;
}
x=xn;
xn=xk;
printf ("k=%d Xk=%.10f Ek=%.10f \n",i,xk,k);
}
printf ("x*=%.10f\n", xk);
}
int main()
{
a=-2;
b=5;
while(1)
{
printf ("\n\n");
printf ("Choose action:\n");
printf ("1-Newton's method\n");
printf ("2-Vegsteyn's method\n");
printf ("3-exit\n");
scanf("%d",&metod);
switch(metod)
{
case 1: newton(a,b);
break;
case 2: vegstein(a,b);
break;
case 3: return 0; break;
defoult: printf("the method is absent");
break;
} }
getch();
}
Результат работы программы:
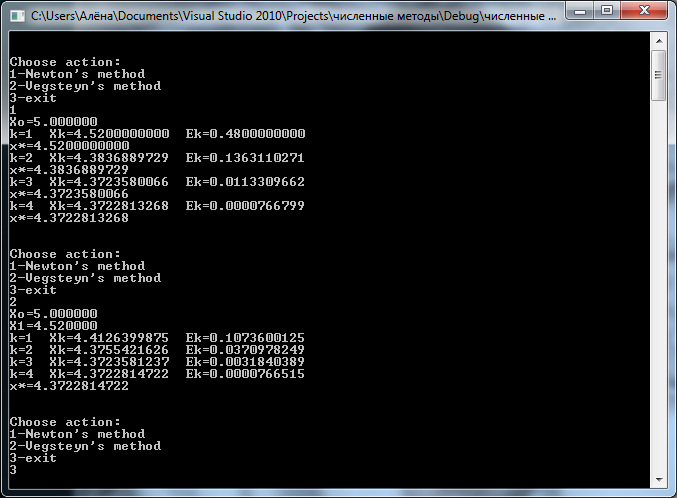
Нахождение корня в Mathcad
 |
 |
 |
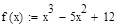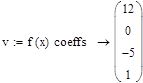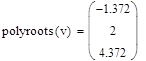
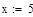Метод Ньютона и Вегстейна практически не отличаются ,единственное отличие в том что производная в методе Вегстейна заменена на
,
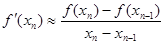Метод Вегстейна является двухшаговым , то есть необходимо знать два предыдущих приближения, что неудобно. Метод Ньютона чувствителен к выбору начального приближения.
Графически проиллюстрируем сходимость метода Ньютона:
| |
 |
 |
 |
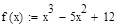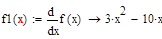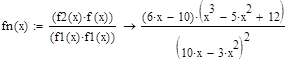Графически проиллюстрируем сходимость метода Вегстейна:
Условие сходимости метода предполагают сохранение знаков f’(x),f”(x) на промежутке [a; b].
 |
Вывод:
В данной работе нашла корень уравнения двумя итерационными методами: Ньютона и Вегстейна. Метод Ньютона одношаговый , поэтому является более приемлемым по сравнению с методом Вегстейна.