Исследование резонанса напряжений в последовательной RLC цепи

Исследование резонанса напряжений в последовательной RLC-цепи

Выполнил: Антоник И.А., студент группы Э-48, ФЭИС, 2 курса

Проверил: Ярошевич А.В.

Брест, 2013 г.

Лабораторная работа №5

Исследование резонанса напряжений в последовательной RLC цепи

Цель работы: исследование параметров последовательной RLC цепи в режиме резонанса цепи и построение амплитудно-частотных характеристик (АЧХ) колебательного контура.

Задание 1

Построение АЧХ контура и определение частоты резонанса

Соберём в программе Electronics Workbench (EWB) схему цепи:

Параметры цепи: Ug = 120 В fg = 20 Гц R = 10 Ом C = 25 мкф L = 2.5 мГн

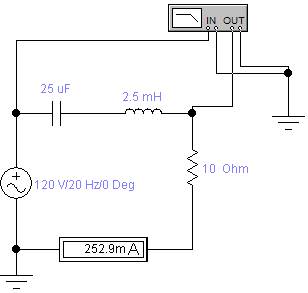
Двойным щелчком мыши раскроем Bode Plotter, предназначенный в режиме Magnitude для построения графика отношения напряжения U_R, отображающего ток цепи I, на входе Out к напряжению U_g на входе In. Этот график характеризует АЧХ контура. Установим на плоттере параметры вертикальной оси: Log для построения графика в логарифмическом масштабе, I = -20 Дб, F = 0 Дб; горизонтальной оси: Log для логарифмического масштаба оси частоты, I = 0.1 Гц, F = 100 кГц.

Запустим моделирование, а затем прервём его. Подводом визира на максимум АЧХ определим резонансную частоту f_рез.

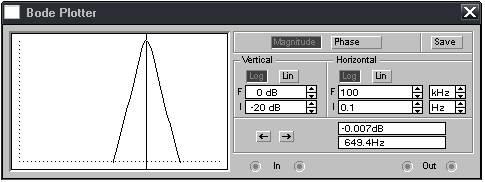
f_рез = 649.4 Гц.

Изменим сопротивление резистора на R = 110 Ом. Запустим и остановим процесс моделирования. Установим визир на максимум АЧХ.

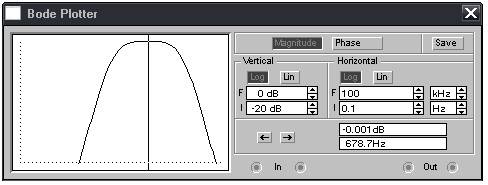
f_рез = 678.7 Гц.

Расчитаем f_рез для цепи:

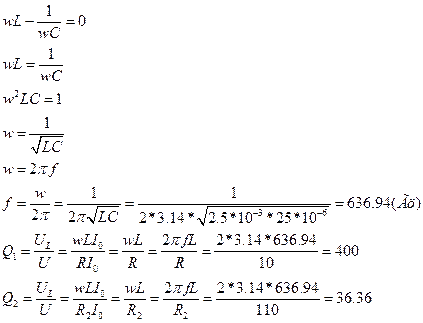
Вывод: частота резонанса в цепи не зависит от сопротивления, включенного в контур, а зависит лишь от ёмкости конденсатора и индуктивности катушки. Чем ниже сопротивление контура, тем выше его добротность, а значит и выше избирательность контура. Чем выше добротность (соответственно меньше R), тем выше и острее резонансная кривая.

Задание 2

Исследование амплитудно-фазовых соотношений колебательного контура

Соберём в программе EWB схему цепи:

Параметры цепи: Ug = 120 В fg = 636 Гц R = 110 Ом C = 25 мкф L = 2.5 мГн

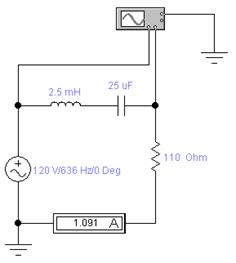
Запустим и остановим процесс моделирования. Осциллограмма:

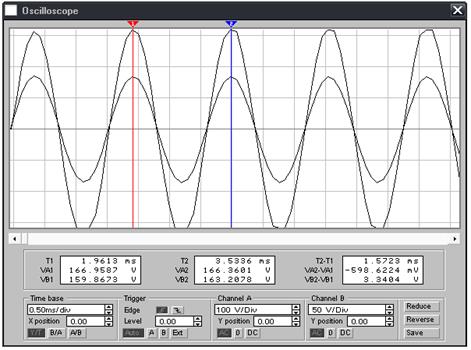
Установим частоту генератора f_g = f_м = 20 Гц.

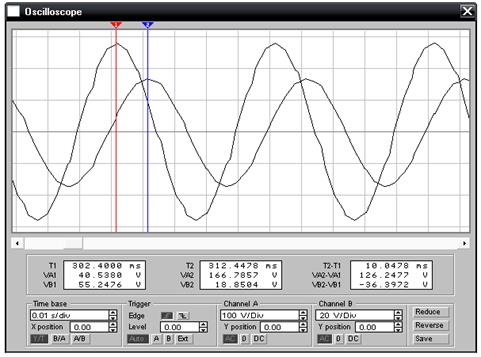
Установим частоту генератора f_g = f_б = 2000 Гц.

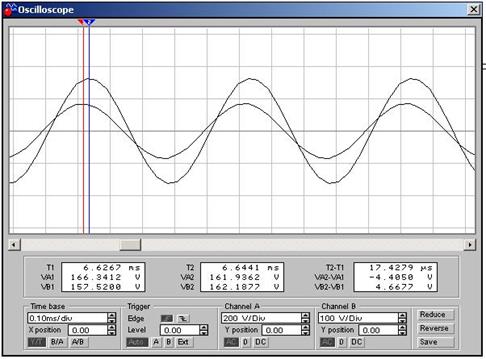
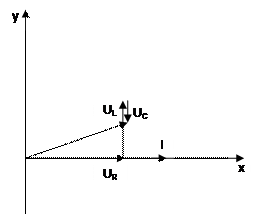
Для частоты f = 636 Гц:

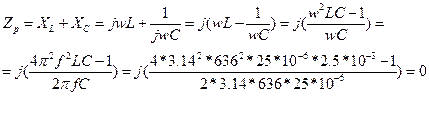
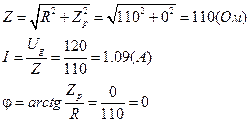
Для частоты f = 20 Гц:

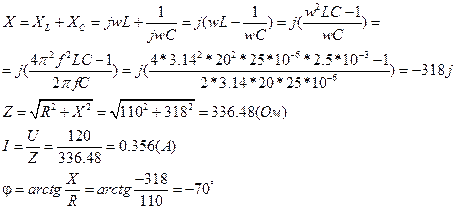
Для частоты f = 2000 Гц:

			Индукционный режим
		Резонанс напряжений

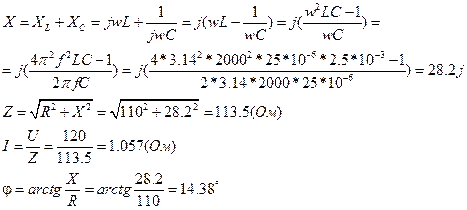
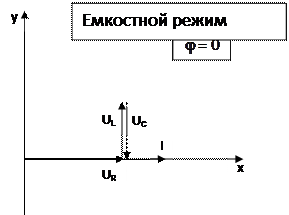
Вывод: в режиме резонанса напряжение на катушке индуктивности равно по модулю напряжению на конденсаторе, реактивное сопротивление цепи равно 0, модуль комплексного сопротивления равен сопротивлению резистора в цепи.

Задание 3

Исследование амплитудно-фазовых соотношений на реактивных элементах контура

Поменяем в предыдущей схеме местами элементы R и C:

Параметры цепи: Ug = 120 В fg = 636 Гц R = 110 Ом C = 25 мкф L = 2.5 мГн

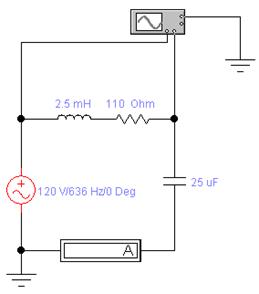
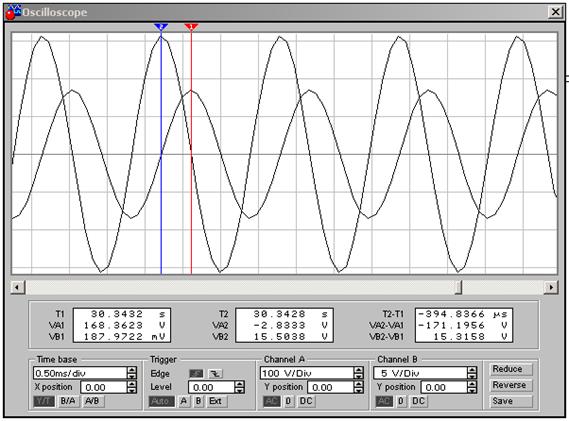
Запустим и остановим процесс моделирования. Канал B отображает мгновенное значение напряжения на конденсаторе U_c.

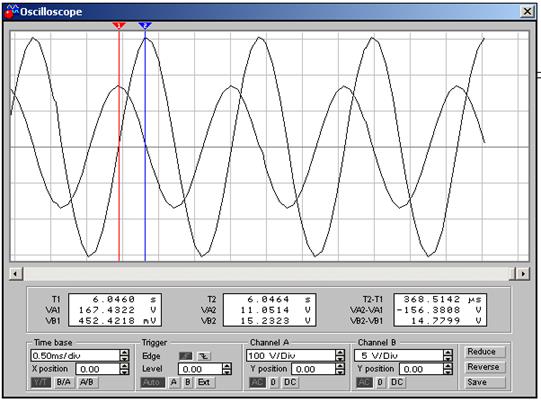
Поменяем в предыдущей схеме L и C местами:

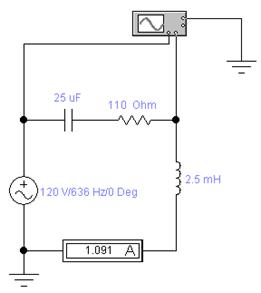
Запустим процесс моделирования и остановим его. Канал B показывает мгновенное значение напряжения на катушке индуктивности U_L.

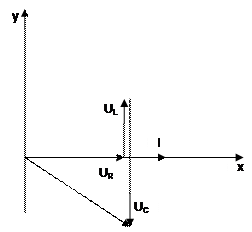
Рассчитаем реактивные сопротивления С и L цепи, амплитудные напряжения:

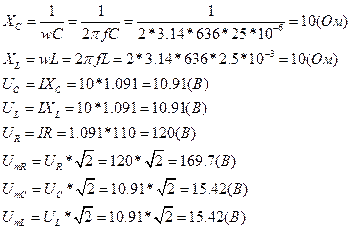
Вывод: при резонансе реактивные сопротивления катушки индуктивности и конденсатора равны. Действующее значение напряжения на резисторе равно напряжению источника питания. Амплитудные значения напряжений совпадают с данными осциллограммы.

Задание 4

Рассчитаем характеристическое сопротивление контура:

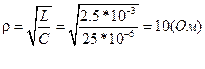
Добротность контура: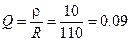

Вывод: чем больше характеристическое сопротивление контура и чем меньше активное сопротивление, тем больше напряжение на реактивных элементах цепи. Чем выше добротность, тем острее и уже резонансная кривая.