Теорема о спектре производной и неопределённого интеграла.

Пусть сигнал 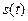и его спектральная плоскость 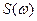заданы. Будем изучать новый сигнал 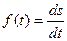и поставим цель найти его спектральную плотность .

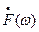По определению:

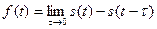(2.14)

Преобразование Фурье – линейная операция, значит, равенство (2.14) справедливо и по отношению к спектральным плотностям. Получаем по теореме о сдвигах:

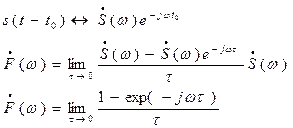(2.15)

Представляя экспоненциальную функцию рядом Тейлора: 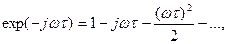подставляя этот ряд в (2.15) и ограничиваясь первыми двумя числами, находим

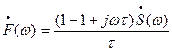
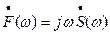(2.16)

Итак, дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель 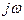. Поэтому говорят, что мнимое число 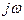является оператором дифференцирования, действующим в частотной области.

Вторая часть теоремы. Рассмотренная функция 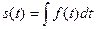является неопределённым интегралом по отношению к функции 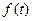. Интеграл это есть 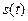, значит 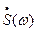- его спектральная плотность, а 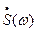из формулы (2.16) равна:

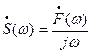(2.17)

Таким образом, множитель служит оператором интегрирования в частотной области.

Физико-геологическая модель разлома, контролируемого зоной дробления, наблюдаемый характер гравитационного и магнитного поля

Основой комплексирования геофизических методов являются физико-геологические модели (ФГМ) геологической среды. Проектирование геофизических работ начинается с постановки целевого задания (в зависимости от стадии геологоразведочного процесса) и выбора объекта исследований. Выбор объекта и определение его основных параметров основано на априорной информации. При выборе комплекса методов, анализе возможностей каждого метода для решения поставленной задачи исследователь абстрагируется от конкретных свойств объекта, используя модель со статистическими усредненными физическими свойствами, формой и геометрией. Г.С. Вахромеевым введено понятие ФГМ. Согласно его определению под ФГМ понимается абстрактное возмущающее тело, обобщенные размеры, форма и контрастность физических свойств которого с той или иной степенью приближения аппроксимируют реальные объекты, подлежащие обнаружению. В качестве ФГМ при геокартировании нередко используют типизированные и формализованные геолого-геофизические разрезы, дополненные сведениями о физических свойствах объектов, слагающих разрез. Такая ФГМ сопровождается расчетными аномалиями физических полей от каждого из элементов разреза. Графически физико-геологические модели изображаются на плоскости в виде разрезов, планов или объемно, блок-диаграммами. ФГМ должна удовлетворять следующим требованиям;

Разлом не нашел((

Экзаменационный билет 10

1) Решение прямой задачи аналитическим методом для сферы

Прямая задача состоит в вычислении значений поля силы тяжести (и, возможно, его производных) в точках над объектом, если известны все параметры объекта (глубина, форма, размеры, плотность). Эта задача, если заданы все параметры объекта, имеет единственное решение и в результате ее решения мы получаем графики поля силы тяжести (V_Z) или (и) ее производных над объектом.

Аналитические решения получается лишь для тел простой геометрической формы (шар, цилиндр и т.д.) с постоянной избыточной плотностью.

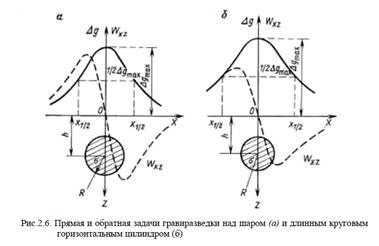
Пусть однородный шар радиусом R,объе­мом V, с избыточной плотностью Δσ расположен на оси Zна глубине h(рис.2.6, а). Ре­шим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним (см. рис.2.6). Поскольку по закону всемирного тяготения шар притягивается с такой же си­лой, как точечная масса, сосредоточенная в его центре, аномалию над шаром Δg_шмож­но получить без решения интеграла (2.26), считая, что аномалия силы тяжести над ша­ром и аномалия точечной массы, помещенной в его центре, совпадают:

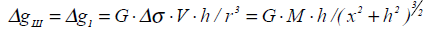(2.27)

гдеM= ΔσV—избыточная масса шара. График Δg_ш будет иметь максимум над центром шара Δg_max=GM/h²(при х=0) и асимптотически стремиться к нулю при X —> ± 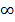(см. рис.2.6, а). Знак Δg_шопределяется знаком Δσ. Формула для второй производной потенциала или горизонтального градиента силы тяжести получает вид

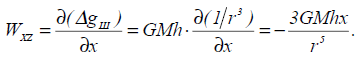(2.28)

График W_Xzимеет перед шаром максимум (х<0), а за шаром — минимум (х>0). Над центром шара Wxz=0(см. рис.2.6, а). Если провести расчеты, например. Ag_mпо ряду профилей, то очевидно, что карта аномалий Δg_шбудет иметь вид концентриче­ских окружностей с центром над шаром.

2) Теорема об интеграле свертки, использование

Теорема о свертке (об интеграле свертки):

Имея функцию P(x) и смещенную на x функцию F₁(x – x), определим интеграл свертки следующим образом:

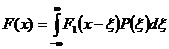. Тогда из соотношений:

дляF(x) Þ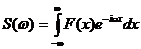

дляF₁(x-x) Þ ,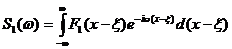

дляP(x) Þ 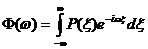естественным образом запишем: 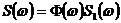, где 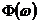представляет собой спектральную характеристику перехода от F(x) к F₁(x-x).

Используют для трансформации геофизических полей (математическоепреобразованиенаблюденныхгеофизическихполейсцельюболееконтрастноговыделенияэффектаоттогоилииногогеологическогообъекта:глубокого, регионального, локального, мелкогоилидлявычислениядругихвеличин, характеризующихполе).

Интеграл свертки также называют интегралом наложения, выраженным через импульсную характеристику цепи.

3) Физико-геологическая модель россыпного месторождения золота, наблюдаемый характер гравитационного и магнитного поля

Золото концентрируется в элювиальных, делювиальных, аллювиальных и прибрежно-морских россыпях, но наибольшее значение имеют аллювиальные, особенно долинные и террасовые россыпи.

Аллювиальные россыпи. Источником золота в этих россыпях являются коренные месторождения, разрушенные в процессе выветривания. Золото, выносимое временными и постоянными водопотоками, отлагается в речных долинах в виде лентообразных, шнурковых, линзо- и гнездообразных тел.

Золото — очень тяжёлый металл: плотность чистого золота равна 19,321 г/м³

Картирование россыпной залежи, вы­явление положения в плане отдельных наиболее перспективных зон возможно с помощью высокоточной детальной магни­тометрической съемки. Золотоносные россыпные залежи имеют в своем составе парамагнитные минералы гематит, ильменит и в очень небольших количествах ферромагнитный магнетит. Ферромагнитные и парамагнитные мине­ралы спутники золота имеют высокую плотность, отлагаются вместе с ним в рос­сыпи и определяют аномальное магнитное поле над нею (Шило, 2002). Поэтому маг­нитометрические исследования с использо­ванием высокоточных магнитометров-градиентометров позволяют выявить уча­стки концентраций тяжелой фракции и, соответственно, золота в рыхлых отложе­ниях потенциально золотоносных долин. При относительно небольших мощностях рыхлых отложений в результате можно оценить геометрические параметры ожи­даемой россыпи.

Экзаменационный билет 11