Роль трансформации в разделении гравитационных и магнитных аномалий.

Билет №1

Роль трансформации в разделении гравитационных и магнитных аномалий.

Ответ:

Под трансформацией здесь понимается некоторое преобразование исходного наблюдаемого поля с целью выделения одних его особенностей и подавления других, менее существенных.

К наиболее важным трансформациям можно отнести следующие преобразования и пересчеты:

1. Осреднение наблюдаемого поля осуществляется чаще всего с целью выделения региональной составляющей наблюдаемого поля. Могут применяться различные приемы осреднения: графические, палеточные, интегральные, аналитические.

2. Преобразования, связанные с получением новых составляющих напряженности поля или их градиентов, осуществляются с применением аналитиче

ских и палеточных методов.

3. Аналитические продолжения предусматривают нахождение значений какой-либо составляющей в некоторой совокупности других точек, т.е. пересчет поля в верхнюю или в нижнюю полуплоскости (полупространство), продолжение поля в боковую область. Аналитическое продолжение поля может быть осуществлено с применением палеточных и аналитических методов, на основе решений интегрального уравнения Пуассона и дифференциального уравнения Лапласа.

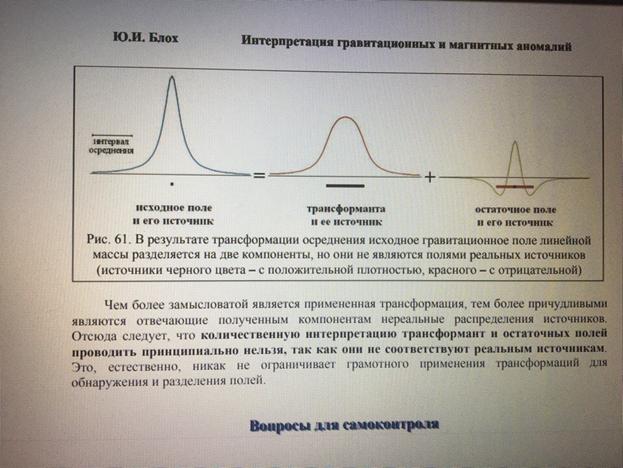
Никакая трансформация не может дать принципиально новых данных, поскольку любая трансформация в лучшем случае не ухудшает исходных данных.

Большинство методов трансформации основано на следующем соответствии порядка геологического объекта и отвечающей ему аномалии: чем крупнее объект и чем глубже он залегает, тем более обширные по площади и малые по градиенту аномалии он создает и наоборот. Первые аномалии называют региональными, а вторые – локальными. Понятие региональных и локальных аномалий является относительным и определяется масштабами съемки.

Любой процесс трансформации гравитационных и магнитных аномалий базируется на преобразованиях Фурье и все интегральные преобразования, применяемые при разделении полей, могут быть представлены в виде интеграла свертки. Существует довольно много способов аналитического продолжения гармонических функций, различающиеся приемами вычисления частных интегралов и выбором пределов интегрирования. Поэтому в практике интерпретации отмечается качественное сходство региональных аномалий, выделенных методом осреднения или пересчета на высоту, и при практической обработке материалов можно ограничиться применением одного из этих методов.

Многие методы выделения локальных аномалий являются естественным дополнением соответствующих методов определения региональных аномалий. Поскольку региональная составляющая поля определена, то, вычитая ее из наблюдаемой аномалии, получают приближенное представление о величине локальной аномалии (остаточной аномалии).

Физический и геометрический смысл производных гравитационного потенциала.

Потенциалом (потенциальной функцией) силового поля называется скалярная функция, частные производные которой по осям прямоугольной системы координат равны проекциям вектора силы на эти оси (А.Лагранж, 1773). Это означает, что

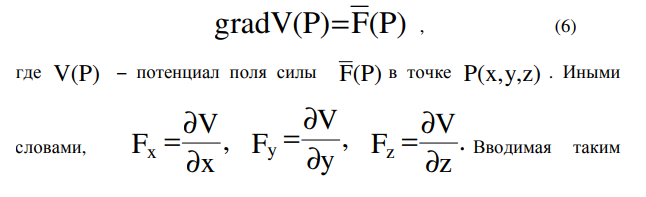
Вводимая таким образом потенциальная функция V(P) позволяет заменить изучение векторного поля F(P) изучением скалярного поля V(P).

Физический смысл потенциала состоит в том, что в любой точке P пространства функция V(P) равна работе, которую требуется совершить против сил поля притяжения, чтобы единичную массу переместить из точки P в бесконечность. Заметим также, что, поскольку замена в функцииV(P) на V(P)+const несущественна, физический смысл имеет не потенциал в отдельной точке, а разность значений потенциалов в двух произвольных точках. Стандартным способом фиксации произвольной аддитивной постоянной является требование V=0 на бесконечности.

Геометрический смысл ХЗ

Билет №2

Билет№ 3

Для тел произвольной формы?

2. понятие трансформации гравитационного и магнитного полей и их роль в интерпретации

Билет 4

Билет №5

Билет №6

1. Решение прямой задачи спектральным методом для тел произвольной формы.

Билет №7

Билет №8

Теорема Сложения сигналов

Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным, очевидно, что при сложении сигналов s1(t), s2(t), обладающих спектрами S1(w), S2(w)… суммарному сигналу s(t)=s1(t)+s2(t)+… соответствует спектр S(w)=S1(w)+S2(w)+….

Теорема смещения

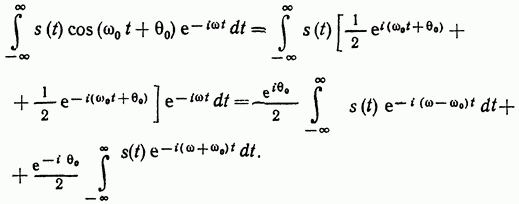
Первый интеграл в правой части есть не что иное, как спектральная плотность функции s(t) при частоте (w--w0), а второй интеграл — при частоте (w+w0). Поэтому полученное выше соотношение можно записать в форме

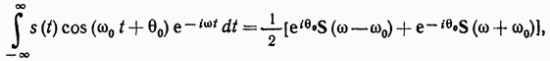2.58

где S(w) — спектральная плотность сигнала s(t).

Из выражения (2.58) вытекает» что расщепление спектра S(w) на две части, смещенные соответственно на +w0 и –w0, эквивалентно умножению функции s(t) на гармоническое колебание cos(w0t).

Экзаменационный билет 10

1) Решение прямой задачи аналитическим методом для сферы

Прямая задача состоит в вычислении значений поля силы тяжести (и, возможно, его производных) в точках над объектом, если известны все параметры объекта (глубина, форма, размеры, плотность). Эта задача, если заданы все параметры объекта, имеет единственное решение и в результате ее решения мы получаем графики поля силы тяжести (V_Z) или (и) ее производных над объектом.

Аналитические решения получается лишь для тел простой геометрической формы (шар, цилиндр и т.д.) с постоянной избыточной плотностью.

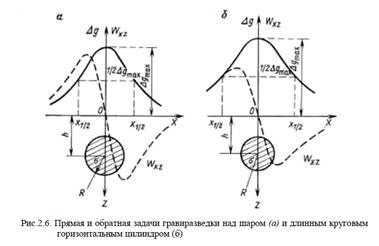
Пусть однородный шар радиусом R,объе­мом V, с избыточной плотностью Δσ расположен на оси Zна глубине h(рис.2.6, а). Ре­шим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним (см. рис.2.6). Поскольку по закону всемирного тяготения шар притягивается с такой же си­лой, как точечная масса, сосредоточенная в его центре, аномалию над шаром Δg_шмож­но получить без решения интеграла (2.26), считая, что аномалия силы тяжести над ша­ром и аномалия точечной массы, помещенной в его центре, совпадают:

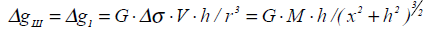(2.27)

гдеM= ΔσV—избыточная масса шара. График Δg_ш будет иметь максимум над центром шара Δg_max=GM/h²(при х=0) и асимптотически стремиться к нулю при X —> ± 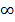(см. рис.2.6, а). Знак Δg_шопределяется знаком Δσ. Формула для второй производной потенциала или горизонтального градиента силы тяжести получает вид

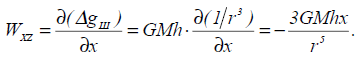(2.28)

График W_Xzимеет перед шаром максимум (х<0), а за шаром — минимум (х>0). Над центром шара Wxz=0(см. рис.2.6, а). Если провести расчеты, например. Ag_mпо ряду профилей, то очевидно, что карта аномалий Δg_шбудет иметь вид концентриче­ских окружностей с центром над шаром.

2) Теорема об интеграле свертки, использование

Теорема о свертке (об интеграле свертки):

Имея функцию P(x) и смещенную на x функцию F₁(x – x), определим интеграл свертки следующим образом:

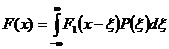. Тогда из соотношений:

дляF(x) Þ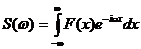

дляF₁(x-x) Þ ,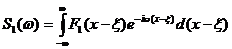

дляP(x) Þ 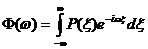естественным образом запишем: 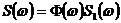, где 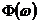представляет собой спектральную характеристику перехода от F(x) к F₁(x-x).

Используют для трансформации геофизических полей (математическоепреобразованиенаблюденныхгеофизическихполейсцельюболееконтрастноговыделенияэффектаоттогоилииногогеологическогообъекта:глубокого, регионального, локального, мелкогоилидлявычислениядругихвеличин, характеризующихполе).

Интеграл свертки также называют интегралом наложения, выраженным через импульсную характеристику цепи.

3) Физико-геологическая модель россыпного месторождения золота, наблюдаемый характер гравитационного и магнитного поля

Золото концентрируется в элювиальных, делювиальных, аллювиальных и прибрежно-морских россыпях, но наибольшее значение имеют аллювиальные, особенно долинные и террасовые россыпи.

Аллювиальные россыпи. Источником золота в этих россыпях являются коренные месторождения, разрушенные в процессе выветривания. Золото, выносимое временными и постоянными водопотоками, отлагается в речных долинах в виде лентообразных, шнурковых, линзо- и гнездообразных тел.

Золото — очень тяжёлый металл: плотность чистого золота равна 19,321 г/м³

Картирование россыпной залежи, вы­явление положения в плане отдельных наиболее перспективных зон возможно с помощью высокоточной детальной магни­тометрической съемки. Золотоносные россыпные залежи имеют в своем составе парамагнитные минералы гематит, ильменит и в очень небольших количествах ферромагнитный магнетит. Ферромагнитные и парамагнитные мине­ралы спутники золота имеют высокую плотность, отлагаются вместе с ним в рос­сыпи и определяют аномальное магнитное поле над нею (Шило, 2002). Поэтому маг­нитометрические исследования с использо­ванием высокоточных магнитометров-градиентометров позволяют выявить уча­стки концентраций тяжелой фракции и, соответственно, золота в рыхлых отложе­ниях потенциально золотоносных долин. При относительно небольших мощностях рыхлых отложений в результате можно оценить геометрические параметры ожи­даемой россыпи.

Экзаменационный билет 11

Билет №12

Билет №13

1. Потенциал однородного намагниченного тела

Для однородно намагниченных тел 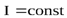и 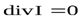, отсюда имеем

.

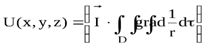Из предыдущего раздела о гравитационном поле потенциал гравитационного поля V, однородного по плотности s тела, имеет вид

.

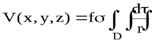Сопоставляя эти два интегральных выражения, находим, что

.

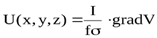Но так как

, ,

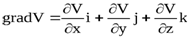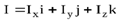то

.

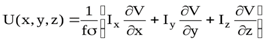Это есть соотношение Пуассона, которое формально устанавливает связь между гравитационным V и магнитным U потенциалами для однородных по плотности и намагниченности тел.

Соотношение Пуассона имеет важное значение в теории и практике интерпретации гравитационных и магнитных аномалий: во-первых, – в количественной интерпретации – методы решения прямых и обратных задач, разработанные для гравиразведки, могут быть использованы в магниторазведке (и обратно); во-вторых, – при решении задач комплексной интерпретации данных гравиразведки и магниторазведки, в частности – при разделении суммарных полей на элементарные поля.

Билет № 14

1.Гравитационный потенциал объекта с однородной плотностью?

Ответ:Все планеты Солнечной системы имеют сферическую форму. Поэтому имеет смысл определить гравитационный потенциал шара. Для упрощения задачи, мы будем предполагать, что плотность шара зависит только от расстояния до его центра Нетрудно убедиться, что такой шар притягивает точно так же, как и материальная точка с массой равной массе шара и помещенная в его центр. Чтобы в этом убедиться, необходимо для формулы (

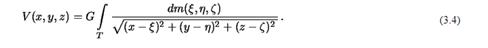выбрать такую систему координат, с помощью которой было бы удобно выполнять интегрирование.

Для начала, представим себе, что точка 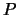находится вне шара. Соединим эту точку с центром шара (точка О), полученный радиус-вектор обозначим через 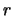. Радиус-вектор элемента массы 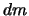будем обозначать буквой 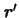. Следовательно расстояние между элементом массы и точкой 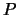, которое мы обозначили греческой буквой 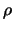, будет иметь вид

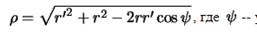
угол с вершиной в центре шара, образованный радиус-векторам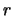и и 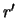. Наконец, элемент массы 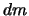определяется произведением плотности на объем элементарно малого параллелепипеда со сторонам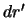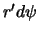и , , и 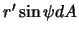. Здесь мы ввели еще одну степень свободы -- поворот вокруг оси 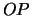на угол 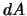. Таким образом,

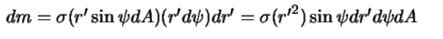
Теперь вместо формулы (3.4) записать

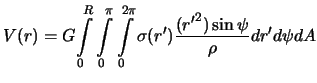(3.5)

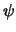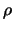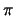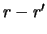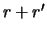Заменим переменную интегрирования на . Определим пределы интегрирования. Очевидно, что вместо 0 и нужно взять и , а 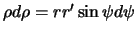. Переменную 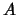подынтегральное выражение не содержит, поэтому внутренний интеграл легко берется. Вместо (3.5) теперь будем иметь

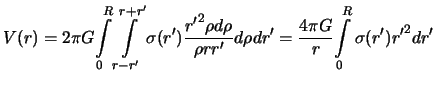Нетрудно догадаться, что 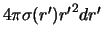есть масса бесконечно тонкой сферы 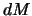, поэтому

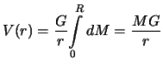(3.7)

Таким образом, мы пришли к очень важному выводу: шар со сферически симметрично распределенной массой притягивает так же, как и материальная точка с массой равной массе шара и помещенной в его центре.

Билет № 15

Билет №20

Билет №21

Билет №1

Роль трансформации в разделении гравитационных и магнитных аномалий.

Ответ:

Под трансформацией здесь понимается некоторое преобразование исходного наблюдаемого поля с целью выделения одних его особенностей и подавления других, менее существенных.

К наиболее важным трансформациям можно отнести следующие преобразования и пересчеты:

1. Осреднение наблюдаемого поля осуществляется чаще всего с целью выделения региональной составляющей наблюдаемого поля. Могут применяться различные приемы осреднения: графические, палеточные, интегральные, аналитические.

2. Преобразования, связанные с получением новых составляющих напряженности поля или их градиентов, осуществляются с применением аналитиче

ских и палеточных методов.

3. Аналитические продолжения предусматривают нахождение значений какой-либо составляющей в некоторой совокупности других точек, т.е. пересчет поля в верхнюю или в нижнюю полуплоскости (полупространство), продолжение поля в боковую область. Аналитическое продолжение поля может быть осуществлено с применением палеточных и аналитических методов, на основе решений интегрального уравнения Пуассона и дифференциального уравнения Лапласа.

Никакая трансформация не может дать принципиально новых данных, поскольку любая трансформация в лучшем случае не ухудшает исходных данных.

Большинство методов трансформации основано на следующем соответствии порядка геологического объекта и отвечающей ему аномалии: чем крупнее объект и чем глубже он залегает, тем более обширные по площади и малые по градиенту аномалии он создает и наоборот. Первые аномалии называют региональными, а вторые – локальными. Понятие региональных и локальных аномалий является относительным и определяется масштабами съемки.

Любой процесс трансформации гравитационных и магнитных аномалий базируется на преобразованиях Фурье и все интегральные преобразования, применяемые при разделении полей, могут быть представлены в виде интеграла свертки. Существует довольно много способов аналитического продолжения гармонических функций, различающиеся приемами вычисления частных интегралов и выбором пределов интегрирования. Поэтому в практике интерпретации отмечается качественное сходство региональных аномалий, выделенных методом осреднения или пересчета на высоту, и при практической обработке материалов можно ограничиться применением одного из этих методов.

Многие методы выделения локальных аномалий являются естественным дополнением соответствующих методов определения региональных аномалий. Поскольку региональная составляющая поля определена, то, вычитая ее из наблюдаемой аномалии, получают приближенное представление о величине локальной аномалии (остаточной аномалии).