Теперь запишем уравнения теоретических линий регрессии

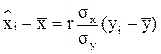Y на X X на Y

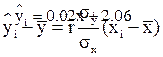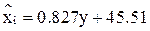Для построения прямых теоретических линий регрессий возмём пары

контрольных точек:

x = 20 x =50 y = 2 y = 4

y = 2.46 y = 3.06 x = 47.17 x = 48.82

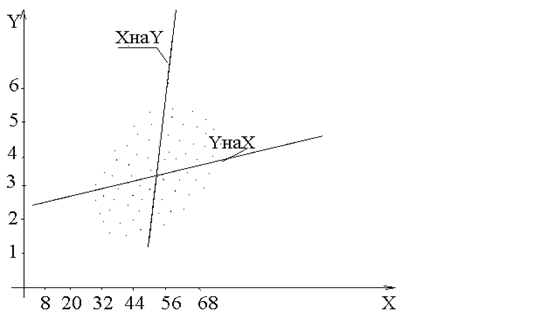Рис 7.4

2. Проверка гипотезы о значимости коэффициента корреляции.

Пусть двумерная случайная величина (Х,Y) распределена по нормальному двумерному закону. Из генеральной совокупности извлечена выборка объёмом N образцов и по этой выборке вычислен выборочный коэффициент корреляцииr_в.

При уровне значимости a требуется проверить нулевую гипотезу о том, что коэффициент корреляции r =0 при конкурирующей гипотезе о том, что r ¹0.

H₀ : r = 0

H_k : r ¹0

Если нулевая гипотеза отвергается, то это означает, что при заданном уровне значимости a выборочный коэффициент корреляции значимо отличается от нуля, а Х и Y коррелированы, т.е. связаны линейной зависимостью.

Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции не значим, а Х и Y некоррелированы, т.е. не связаны линейной зависимостью.

В качестве критерия проверки нулевой гипотезы примем случайную величину :

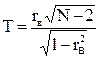(7.5)

Эта случайная величина распределена по закону Стьюдента с k = (N – 2) степенями свободы.

Поскольку конкурирующая гипотеза имеет вид r ¹0, критическая область – двусторонняя.

Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н₀: r = 0 о равенстве нулю коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе о том, что он не равен нулю H_k : r ¹0,надо вычислить наблюдаемое значение критерия:

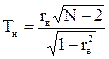(7.6)

Затем по таблице критических точек распределения Стьюдента, по заданному уровню значимости a и числу степеней свободы k = N – 2

в соответствии со стратегией Неймана-Пирсона найти критическую точку t_кр (a,k).

Правило принятия решения будет следующим :

Если | Т_H |< t_кр – нет оснований отвергать нулевую гипотезу

Если | Т_H |> t_кр –нулевую гипотезу отвергают.

Если нулевая гипотеза отвергнута, значит отличие коэффициента корреляции r от нуля при заданном уровне значимости носит закономерный характер. Если же мы приняли нулевую гипотезу, следовательно отличие коэффициента корреляции r от нуля при заданном уровне значимости носит случайный характер.

Пример:

Вычислим значение Т_н : Т_н= 0.7359

Значение t_кр найдем по таблице распределения критических точек Стьюдента .

Для a = 0.05 и k = 32 оно равно: t_кр = 2.04

Очевидно, что | Т_H |< t_кр

Используя стратегию Неймана – Пирсона, делаем вывод, что нет оснований отвергать нулевую гипотезу о том, что r = 0. Иными словами, при заданном уровне значимости отклонение коэффициента корреляции от нуля носит случайный характер.

Вопросы к седьмой лабораторной работе.

1.В чём смысл работы?

2. В чём суть метода наименьших квадратов?

3. Дать определение статистической и корреляционной зависимости.

4. Написать формулы для восьмой лабораторной работы.

Лабораторная работа №8

Фильтрация поля скользящим окном

.1. Случайные функции и их характеристики

Геологические модели исследуемого геологического пространства создаются на основе анализа комплексной геологической информации. Среди этой информации важное место занимают геологические, геохимические и геофизические поля, полученные в результате геологических, геохимических и геофизических съемок различного уровня, документации и каратажа скважин и др.

Случайной называют функцию, которая в результате испытания принимает тот или иной конкретный вид, заранее неизвестно какой именно.

Случайные функции - это упорядоченные по времени или пространству случайные величины. Примерами случайных функций в геологической практике, как уже отмечалось, являются: результаты опробования горных выработок, измерения геофизических или геохимических полей, измерения вариаций магнитного поля в течение дня, данные каратажа и документации скважин и др.

Случайная функция, аргументом которой является время, называется случайным процессом F(t).

Случайная функция, аргументом которой является координаты пространства, называется случайным полем F(x).

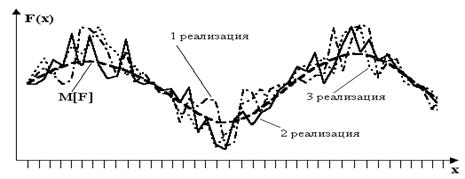Каждый конкретный вид, который принимает случайная функция в результате испытания, называется ее реализацией.

Рис1.1

При проведении серии испытаний получают семейство реализаций случайной функции. Примером такого семейства являются контрольные измерения геофизического поля по одному и тому же профилю. Рис. 1.1.

Совокупность значений случайной функции для любого фиксированного значения аргумента x_j называется сечением случайной функции и является обычной случайной величиной F(x_j).

Для этой случайной величины можно вычислить математическое ожидание M[F(x_j)], дисперсию D[F(x_j)] и другие характеристики, построить функцию плотности распределения f_Fj и т.д. Если вычислить математическое ожидание и дисперсию для каждого значения аргумента х случайной функции, получим математическое ожидание M[F] и дисперсию D[F] случайной функции.

Математическое ожидание случайной функции характеризует некоторую среднюю функцию, вокруг которой колеблются все ее реализации.

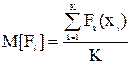(1.1)

Дисперсия случайной функции характеризует разброс реализаций относительно математического ожидания случайной функции.

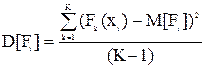(1.2)

Здесь: F_k(x_i) - реализация случайной функции

K - количество реализаций.