Интервальные оценки параметров распределения

(доверительные интервалы).

Пусть дана генеральная совокупность X, из которой извлечены несколько выборок и для каждой выборки вычислена оценка :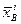

1-ая выборка , ,...,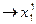

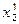2-ая выборка , ,...,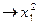

.................................................

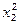k-ая выборка , ,...,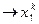

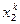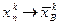
Все выборочные средние оценивают одно и то-же математическое ожидание M(X). Ясно, что 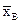тем точнее определяет оцениваемый параметр, чем меньше абсолютная величина разности 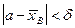. Другими словами, если 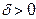и, то чем меньше 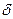, тем оценка точнее. Таким образом положительное число 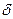характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка 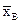удовлетворяет неравенству 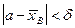; можно лишь говорить о вероятности , с которой это неравенство осуществляется.

Определение 3.1

Надёжностью (доверительной вероятностью) оценки 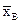называется вероятность 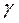, с которой осуществляется неравенство .

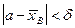Надёжность обычно задаётся числом близким к единице 0.9, 0.95 или 0.99.

Пусть вероятность того, что 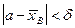, равна :

.

Раскрывая модуль 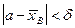получим двойное неравенство .

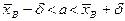Тогда

.

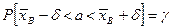Это соотношение следует понимать как вероятность того, что неизвестный параметр a находится в интервале , которая равна .

Определение 3.2

Доверительным называется интервал который с заданной надёжностью включает в себя истинное значение математического ожидания a .

1. Доверительный интервал для математического ожидания нормального распределения признака при неизвестном s.

Пусть X распределён по нормальному закону с параметрами a и , которые неизвестны.

Тогда для вероятности попадания истинного значения математического ожидания в интервал можем написать:

(3.2)

где значение - распределёно по закону Стьюдента и табулировано, его значение можно найти, зная и N по таблице Приложения №3 (1).

2. Доверительный интервал для среднеквадратического отклонения s нормально распределённого признака.

Пусть существует генеральная совокупность, в которой изучается признак X, распределённый по нормальному закону . Определим доверительный интервал для среднеквадратического отклонения s по заданному уровню значимости и стандарту s.

Преобразуем двойное неравенство

.

Положив =q, получим

,

где q можно найти по таблице значений q = q (g, N) приложения №4, зная и объём выборки N.

Смысл полученного выражения состоит в том, что с надёжностью можно утверждать, что истинное значение среднеквадратического отклонения s находится в интервале .

Рассмотрим сквозной пример.

Пусть признак X распределён по нормальному закону. Известно, что объём выборки N=50, s=2.4, . Построить доверительный интервал для математического ожидания a и среднего квадратического отклонения s с заданным уровнем значимости =0.95.

Решение:

1. Вычислим доверительный интервал для математического ожидания a:

Зная N=50 и =0.95, по таблицам приложения №3 найдём =2.009.

15.04- <a<15.04+

14.35<a<15.72

Вывод: С надежностью 0.95 можно утверждать, что истинное значение математического ожидания попадет в интервал (14.35; 15.72).

2. Вычислим доверительный интервал для среднего квадратического отклонения s:

Зная N=50 и =0.95, по таблицам приложения №4 найдём q=0.21.

Вывод: С надежностью 0.95 можно утверждать, что среднеквадратическое отклонение попадет в интервал (1.89 ; 2.9).

Вопросы к 3-ей лабораторной работе.

1.В чём смысл работы?

2. В чём смысл доверительного интервала?

3. Написать формулы третьей лабораторной работы.

4. Как будет вести себя интервал с увеличением надежности?

Лабораторная работа №4.