Выборочный метод, построение интегральной и дифференциальной функций распределения.
Геолога в первую очередь интересуют приемы сбора и обработки информации, определения статистических характеристик изучаемых признаков.
Определение 1.1
Множество однородных объектов, подлежащих статистическому изучению, называется статистической совокупностью.
В качестве статистической совокупности, которую называют генеральной, могут выступать горные породы. Тогда элементами этой совокупности будут образцы горных пород. Горные породы можно охарактеризовать различными свойствами (признаками). Среди которых могут быть: плотность пород, магнитная восприимчивость, сопротивление, содержание химических элементов и другие.
Изучить всю генеральную совокупность принципиально невозможно или практически нецелесообразно. (Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла).
Поэтому прибегают к выборочному методу, суть которого состоит в том, что из генеральной совокупности отбирают сравнительно небольшую выборку объемом N образцов, изучают ее по интересующему исследователя признаку, а затем на основании анализа выборки делают вывод обо всей генеральной совокупности.
Пример:
Дана выборка (объемом N =50) образцов горных пород, в каждом из которых определено содержание Аl2О3 в процентах.
Результаты измерений приведены в таблице:
| 15.1 | 18.7 | 14.3 | 16.1 | 12.8 |
| 14.7 | 19.1 | 15.5 | 13.5 | 15.1 |
| 16.7 | 11.2 | 13.4 | 12.4 | 14.7 |
| 17.2 | 13.6 | 12.7 | 13.7 | 17.3 |
| 15.2 | 12.2 | 16.2 | 14.9 | 15.6 |
| 14.1 | 20.6 | 14.9 | 13.2 | 14.2 |
| 16.4 | 18.3 | 17.4 | 12.3 | 16.9 |
| 17.8 | 12.8 | 21.8 | 14.8 | 17.7 |
| 9.1 | 14.6 | 13.8 | 10.8 | 13.1 |
| 12.1 | 15.7 | 15.4 | 14.7 | 15.6 |
Требуется построить эмпирические дифференциальную и интегральную функции распределения.
Решение поставленной задачи разобьем на этапы:
1) Определим интервал группирования.
Величину частичного интервала группирования можно приближенно оценить формулой Стирлинга.
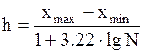 |
Здесь
хmax - максимальное значение признака в выборке.
хmin - минимальное значение признака в выборке.
N - объем выборки.
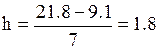 |
В нашем случае хmax = 21.8 хmin = 9.1 N = 50, тогда:
Поскольку число интервалов выбирается произвольно, ориентируясь на полученное значение, примем в качестве интервала группирования величину близкую, но более удобную, равную двум.
Таким образом: h » 2.
2) Разобьем весь интервал изменения измеренного признака на частичные интервалы длиной h = 2.
Для этого левая граница первого частичного интервала выбирается меньше минимального числа. То есть, например, 8.
Тогда интервалы группирования примут следующие значения:
(8..10)(10..12)(12..14)...(20..22).
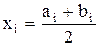 |
Найдем середины интервалов по формуле
Где аi - левая граница соответствующего интервала группирования;
b i - правая граница соответствующего интервала группирования.
3) Вычислим частоту попадания измеряемой величины в каждый интервал n i.
Для этого определим, сколько образцов горных пород имеют значения изучаемого признака
от 8 до 10, таких 1;
от 10 до 12, таких 2;
от 12 до 14, таких 14 и так далее.
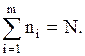 Сумма всех частот должна быть равна объему выборки согласно формуле (11.2).
Сумма всех частот должна быть равна объему выборки согласно формуле (11.2).
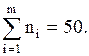
В нашем случае
m- количество интервалов группирования,
Вычислим относительные частоты, плотность относительных частот и накопленные относительные частоты.
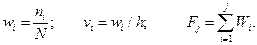
Результаты сведём в таблицу:
| Интервал | x i | n i | w i | v i | 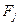 |
| 8..10 10..12 12..14 14..16 | 0.02 0.04 0.28 0.36 | 0.01 0.02 0.14 0.18 | 0.02 0.06 0.34 0.70 | ||
| 16.. 18 | 0.20 | 0.10 | 0.90 | ||
| 18..20 | 0.06 | 0.03 | 0.96 | ||
| 20..22 | 0.04 | 0.02 | 1.0 |
Sn i =50 Sw i =1.0
4) На основании полученных результатов строим гистограммы.
Определение 1.2
Гистограммой, плотности относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиною h, а высотами - плотности относительных частот
v i =w i/h (1.1)
По гистограмме плотности относительных частот строят эмпирическую дифференциальную функцию распределения fэ(x), соединяя плавной линией середины верхних площадок прямоугольников.
Определение 1.3
Гистограммой накопленных относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиною h, а высоты равны значению накопленных относительных частот.
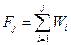 (1.2)
(1.2)
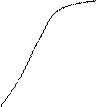
По гистограмме накопленных относительных частот строят эмпирическую интегральную функцию распределения Fэ (x), соединяя
плавной линией правые верхние углы прямоугольников в соответствии с определением интегральной функции.
Fi 



 1.0
1.0
0.8
 0.6
0.6
0.4
 0.2
0.2

8 10 12 14 16 18 20 22 X
 Vi
Vi
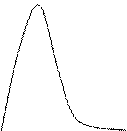
 0.2
0.2
0.15
 |
 0.1
0.1
0.05
 |
8 10 12 14 16 18 20 22 X
Вопросы к первой лабораторной работе.
1. В чём смысл работы?
2. В чём суть выборочного метода?
3. Написать формулы и дать определения, которые использовались в первой лабораторной работе?.
4.Почему при построении интегральной функции сглаживающую линию проводим через правые точки верхних площадок?
5. Чему равна площадь ограниченная дифференциальной функцией?
Лабораторная работа №2.
