Учебное пособие по выполнению

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ

Кафедра МАТЕМАТИКИ

ЛАБОРАТОРИЯ КОМПЬЮТЕРНЫХ СРЕДСТВ ОБУЧЕНИЯ

В. А. СИКОРСКИЙ

СТАТИСТИКА

УЧЕБНОЕ ПОСОБИЕ ПО ВЫПОЛНЕНИЮ

ЛАБОРАТОРНЫХ РАБОТ

МОСКВА 2017 г.

Лабораторная работа №1.

Выборочный метод, построение интегральной и дифференциальной функций распределения.

Геолога в первую очередь интересуют приемы сбора и обработки информации, определения статистических характеристик изучаемых признаков.

Определение 1.1

Множество однородных объектов, подлежащих статистическому изучению, называется стати­стической совокупностью.

В качестве статистической совокупности, которую называют генеральной, могут выступать горные породы. Тогда элементами этой совокупности будут образцы горных по­род. Горные породы можно охарактеризовать различными свойствами (признаками). Среди которых могут быть: плотность пород, магнитная восприимчивость, сопротивление, содержание химических элементов и другие.

Изучить всю генеральную совокупность принципиально невозможно или практически нецелесообразно. (Например, если совокупность содержит очень большое число объектов, то провести сплошное обследо­вание физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла).

Поэтому прибегают к выборочному методу, суть которого состоит в том, что из генеральной совокупности отбирают сравнительно небольшую выборку объемом N образцов, изучают ее по интересующему исследователя признаку, а затем на основании ана­лиза выборки делают вывод обо всей генеральной совокупности.

Пример:

Дана выборка (объемом N =50) образцов горных пород, в каждом из которых определено содержание Аl₂О₃ в процентах.

Результаты измерений приведены в таблице:

15.1	18.7	14.3	16.1	12.8
14.7	19.1	15.5	13.5	15.1
16.7	11.2	13.4	12.4	14.7
17.2	13.6	12.7	13.7	17.3
15.2	12.2	16.2	14.9	15.6
14.1	20.6	14.9	13.2	14.2
16.4	18.3	17.4	12.3	16.9
17.8	12.8	21.8	14.8	17.7
9.1	14.6	13.8	10.8	13.1
12.1	15.7	15.4	14.7	15.6

Требуется построить эмпирические дифференциальную и интегральную функции распределения.

Решение поставленной задачи разобьем на этапы:

1) Определим интервал группирования.

Величину частичного интервала группирования можно приближенно оценить формулой Стирлинга.

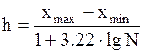Здесь

х_max - максимальное значение признака в выборке.

х_min - минимальное значение признака в выборке.

N - объем выборки.

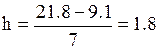В нашем случае х_max = 21.8 х_min = 9.1 N = 50, тогда:

Поскольку число интервалов выбирается произвольно, ориентируясь на полученное значение, примем в качестве интервала группирования ве­личину близкую, но более удобную, равную двум.

Таким образом: h » 2.

2) Разобьем весь интервал изменения измеренного признака на частичные интервалы длиной h = 2.

Для этого левая граница первого частичного интервала выбирается меньше минимального числа. То есть, например, 8.

Тогда интервалы группирования примут следующие значения:

(8..10)(10..12)(12..14)...(20..22).

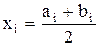Найдем середины интервалов по формуле

Где а_i - левая граница соответствующего интервала группирования;

b _i - правая граница соответствующего интервала группирования.

3) Вычислим частоту попадания измеряемой величины в каждый ин­тервал n _i.

Для этого определим, сколько образцов горных пород имеют значения изучаемого признака

от 8 до 10, таких 1;

от 10 до 12, таких 2;

от 12 до 14, таких 14 и так далее.

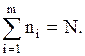Сумма всех частот должна быть равна объему выборки согласно фор­муле (11.2).

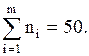
В нашем случае

m- количество интервалов группирования,

Вычислим относительные частоты, плотность относительных час­тот и накопленные относительные частоты.

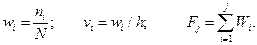
Результаты сведём в таблицу:

Интервал	x i	n i	w i	v i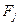
8..10 10..12 12..14 14..16			0.02 0.04 0.28 0.36	0.01 0.02 0.14 0.18	0.02 0.06 0.34 0.70
16.. 18			0.20	0.10	0.90
18..20			0.06	0.03	0.96
20..22			0.04	0.02	1.0

Sn _i =50 Sw _i =1.0

4) На основании полученных результатов строим гистограммы.

Определение 1.2

Гистограммой, плотности относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиною h, а высотами - плотности от­носительных частот

v _i =w _i/h (1.1)

По гистограмме плотности относительных частот строят эмпирическую дифференциальную функцию распределения f_э(x), соеди­няя плавной линией середины верхних площадок прямоугольников.

Определение 1.3

Гистограммой накопленных относительных час­тот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых явля­ются частичные интервалы длиною h, а высоты равны значению накопленных относительных час­тот.

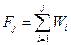(1.2)

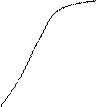
По гистограмме накопленных относительных частот строят эмпирическую интегральную функцию распределения F_э (x), соединяя

плавной линией правые верхние углы прямоугольников в соответствии с определением интегральной функции.

F_i

1.0

0.8

0.6

0.4

0.2

8 10 12 14 16 18 20 22 X

V_i

0.2

0.15

0.1

0.05

8 10 12 14 16 18 20 22 X

Вопросы к первой лабораторной работе.

1. В чём смысл работы?

2. В чём суть выборочного метода?

3. Написать формулы и дать определения, которые использовались в первой лабораторной работе?.

4.Почему при построении интегральной функции сглаживающую линию проводим через правые точки верхних площадок?

5. Чему равна площадь ограниченная дифференциальной функцией?

Лабораторная работа №2.

Определение 2.3

Оценка называется состоятельной, если она стремится по вероятности к оцениваемому параметру при .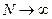

Оценками математического ожидания являются:

выборочная средняя, мода и медиана.

Определение 2.4

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности:

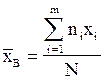(2.1),

где:

n- количество интервалов группирования,

x­_i -середина интервала группирования,

n­­_i- частота попадания в интервал группирования,

N - объём выборки.

Выборочная средняя есть несмещённая, эффективная и состоятельная оценка математического ожидания.

Определение 2.5

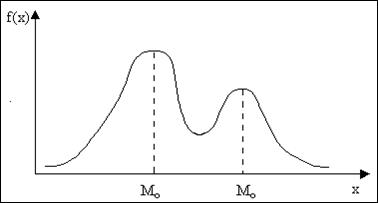Мода (M₀) это абсцисса экстремума эмпирической дифференциальной функции распределения.

Определение 2.6:

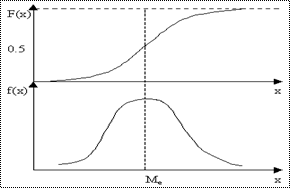Медиана (M_e) это абсцисса линии, которая делит площадь ограниченную дифференциальной функцией на две равные части.

Оценками дисперсии являются:выборочная дисперсия и квадрат стандарта.

Определение 2.7

Выборочной дисперсией называют среднее арифметическое квадратов отклонений наблюдаемого значения признака от своего выборочного:

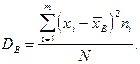(2.2)

Выборочная дисперсия является смещённой оценкой дисперсии, несмещённой оценкой дисперсии является квадрат стандарта:

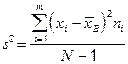. (2.3)

Оценкой среднеквадратического отклонения является стандарт s .

Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, в том числе асимметрию и эксцесс.

Определение 2.8

Асимметрией называется оценка центрального момента третьего порядка, делённая на s³.

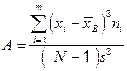. (2.4)

Она характеризует различия в крутизне

склонов графика эмпирической дифференциальной функции распределения.

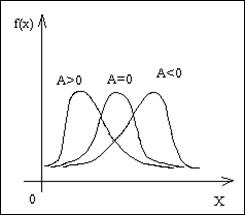Если X распределён по нормальному закону, асимметрия A=0. Если A>0, тогда правая ветвь дифференциальной функции пологая, а левая ветвь крутая. Если A<0, тогда правая ветвь дифференциальной функции крутая, а левая ветвь пологая.

Определение2.9

Эксцессом называется оценка центрального момента четвёртого порядка, делённая на s⁴ и минус 3.

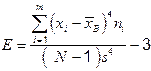. (2.5)

Она характеризует различия в крутизне

вершины графика эмпирической дифференциальной функции распределения.

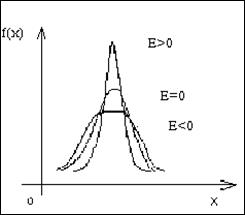Если X распределён по нормальному закону, тогда E=0.

Рассмотрим сквозной пример.

Пусть дана генеральная совокупность, из которой извлечена выборка объёмом N=50:

15.1 18.7 14.3 16.1 12.8 14.7 19.1 15.5 13.5 15.5

16.7 11.2 13.4 12.4 14.7 17.2 13.612.7 13.7 17.3

15.2 12.2 16.2 14.9 15.6 14.1 20.6 14.9 13.2 14.2

16.4 18.3 17.4 12.3 16.9 17.8 12.8 21.8 14.8 17.7

9.1 14.6 13.8 10.8 13.1 12.1 15.7 15.4 14.7 15.6

Для этой выборки известны

x­_i -середины интервалов группирования,

n­­_i- частота попадания в интервал группирования (см. §1).

Найдём 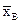, s², A, E.

Решение:

Найдём выборочную среднюю.

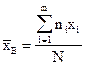
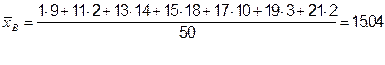
Заполним таблицу:

x­­­­i	x­i- 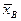=t	t2	t3	t4	ni
	-6.04	36.48	-220.34	1330.97
	-4.04	16.32	-65.93	266.35
	-2.04	4.16	-8,49	17,32
	0.04	0.0016	0.000064	0.00000256
	1.96	3.84	7.53	14.76
	3.96	15.68	62.09	245.91
	5.9	34.81	205.38	1211.74

Вычислим квадрат стандарта.

.

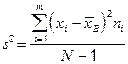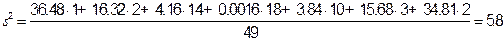
Стандарт равен: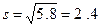

Вычислим асимметрию.

.

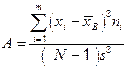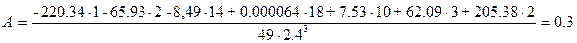
Вычислим эксцесс.

.

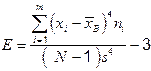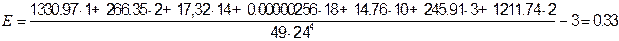
Вопросы ко второй лабораторной работе.

1. В чём смысл работы?

2. Какие параметры распределения Вы знаете?

3. Какие оценки параметров распределения Вы знаете?

5. Написать формулы для второй лабораторной работы и сказать, что они характеризуют.

6. Дать определения характера оценок из второй лабораторной работы.

7. Показать на графике оценки математического ожидания.

Лабораторная работа №3.

Определение 3.2

Доверительным называется интервал который с заданной надёжностью включает в себя истинное значение математического ожидания a .

1. Доверительный интервал для математического ожидания нормального распределения признака при неизвестном s.

Пусть X распределён по нормальному закону с параметрами a и , которые неизвестны.

Тогда для вероятности попадания истинного значения математического ожидания в интервал можем написать:

(3.2)

где значение - распределёно по закону Стьюдента и табулировано, его значение можно найти, зная и N по таблице Приложения №3 (1).

2. Доверительный интервал для среднеквадратического отклонения s нормально распределённого признака.

Пусть существует генеральная совокупность, в которой изучается признак X, распределённый по нормальному закону . Определим доверительный интервал для среднеквадратического отклонения s по заданному уровню значимости и стандарту s.

Преобразуем двойное неравенство

.

Положив =q, получим

,

где q можно найти по таблице значений q = q (g, N) приложения №4, зная и объём выборки N.

Смысл полученного выражения состоит в том, что с надёжностью можно утверждать, что истинное значение среднеквадратического отклонения s находится в интервале .

Рассмотрим сквозной пример.

Пусть признак X распределён по нормальному закону. Известно, что объём выборки N=50, s=2.4, . Построить доверительный интервал для математического ожидания a и среднего квадратического отклонения s с заданным уровнем значимости =0.95.

Решение:

1. Вычислим доверительный интервал для математического ожидания a:

Зная N=50 и =0.95, по таблицам приложения №3 найдём =2.009.

15.04- <a<15.04+

14.35<a<15.72

Вывод: С надежностью 0.95 можно утверждать, что истинное значение математического ожидания попадет в интервал (14.35; 15.72).

2. Вычислим доверительный интервал для среднего квадратического отклонения s:

Зная N=50 и =0.95, по таблицам приложения №4 найдём q=0.21.

Вывод: С надежностью 0.95 можно утверждать, что среднеквадратическое отклонение попадет в интервал (1.89 ; 2.9).

Вопросы к 3-ей лабораторной работе.

1.В чём смысл работы?

2. В чём смысл доверительного интервала?

3. Написать формулы третьей лабораторной работы.

4. Как будет вести себя интервал с увеличением надежности?

Лабораторная работа №4.

Рис. 4.1

Определение 4.2

Ошибкой второго рода называется cобытие, состоящее в том, что мы принимаем нулевую гипотезу в то время, как на самом деле она не верна.

В общем виде:

(4.3)

Если х распределен по нормальному закону, и извесны его математическое ожидание и среднеквадратическое отклонение , то

(4.4)

Определение 4.3

(1 – β) называется мощностью крите-

рия.

2. Разделение горных пород на два класса

В геологической практике при поисках и разведке полезных ископаемых постоянно возникает задача классификации объектов на два класса. Это может быть разделение объектов на рудные и безрудные, выделение одной горной породы на фоне другой, выделение геохимических аномалий, связанных с определенными геологическими явлениями среди других геохимических аномалий.

Во всех случаях мы сталкиваемся с задачей разделения объектов на два класса по изучаемому признаку.

Обычно задача классификации состоит из двух этапов.

На первом этапе (этапе обучения) по выборкам из имеющихся двух классов на эталонных объектах, определяется решающее правило, а также ошибки и надежность классификации.

На втором этапе классифицируют уже неизвестные объекты по изучаемому признаку, т.е относят их к тому или иному классу в соответствии с выработанным критерием.

Итак, пусть имеется два класса горных пород, в которых изучается какое-либо свойство. И пусть взяты выборки из каждого класса

R1

f2(x)

x

xk

β

α

R2

f1(x)

f(x)

на этапе обучения. В результате анализа данных двух выборок построены эмпирические функции плотности распределения каждого класса.

Рис 4.1

При проведении геологических работ необходимо по измеряемому параметру Х отнести образцы горной породы к одному, либо к другому классу.

Таким образом, выдвигаются две гипотезы:

Гипотеза H₁ - образец горной породы относится к I классу.

Гипотеза H₂ - образец горной породы относится ко 2 классу.

Будем полагать, что нам известны априорные (известные до опыта) вероятности встречи горной породы в районе (вероятности гипотез) P(H1) и P(H₂).

P(H₁)+P(H₂)=1

При выборе x_k, т.е. при разделении пространства признака Х на два (R₁ и R₂) необходимо учитывать, с чем сопряжено совершение ошибок 1 и 2 рода.

Пусть С₁₂- стоимость ошибки первого рода,

С₂₁- стоимость ошибки второго рода,

С₁₁ и С₂₂ - стоимости правильных решений.

Вероятности правильных решений вычисляются по формулам:

;

Тогда средняя стоимость, которую приходится платить при многократном распознавании неизвестных объектов, равна сумме стоимостей неправильных и правильных решений с учетом вероятностей их появлений и априорных вероятностей.

(4.4)

Определение 4.4

Отношение плотностей вероятностей называется коэффициентом правдоподобия.

Если С₁₁ = С₂₂ = 0, т.е. если нет затрат на правильное решение,

С₁₂ = С₁, а С₂₁ = С₂, отношение правдоподобия равно:

(4.5)

При одинаковых стоимостях ошибок С₁ = С₂ .

Критерий Кательникова

Если же априорные вероятности равны P(H₁) = P(H₂) = 0.5, то

Критерий максимального правдоподобия

Следовательно, в этом случае x_k есть абсцисса точки пересечения дифференциальных функций распределения f₁(x) и f₂(x).

1. Область R₁ состоит из значений х, для которых <1, при этом x < x_k.

2. Область R₂ состоит из значений х, для которых >1, при этом х > x_k.

Определение 4.5

Стратегия решений, при которой критическая точка выбирается так, что минимизирует средний риск (средняя стоимость) называется стратегией Байеса.

Рассмотрим пример разделения горных пород на два класса по изучаемому признаку.

Пусть в некотором районе имеются два класса пегматитов - рудные и безрудные. На хорошо геологически изученных участках из каждого класса пегматитов взяты выборки, в которых изучено какое-либо свойство Х. Полученные данные обработаны: для каждой выборки определены эмпирические функции распределения и функции плотности распределения. Результаты обработки сведены в таблицы.

1 класс.

	ni	Wi	Vi	Fi
8-10		0,02	0,01	0,02
10-12		0,04	0,02	0,06
12-14		0,28	0,14	0,34
14-16		0,36	0,18	0,70
16-18		0,20	0,10	0,90
18-20		0,06	0,03	0,96
20-22		0,04	0,02	1,00

2 класс

	ni	Wi	Vi	Fi
8,2-9,4		0,04	0,033	0,04
9,4-10,6		0,18	0,150	0,22
10,6		0,32	0,267	0,54
11,8-13,0		0,28	0,233	0,82
13,0-14,2		0,16	0,133	0,98
14,2-15,4		0,02	0,017	1,00

	xk

V2

V2

a

b

β=0,13

b

a

V2

x

Fэ

α=0,24

Vi

x

Vi

Рис.4.2

По полученным данным требуется установить решающее правило (критерий разделения пород на два класса по изучаемому признаку) и оценить ошибки диагностики при массовом распознавании образцов пегматитов. Фактически, изучив свойство Х образца, взятого из исследуемого пегматитового тела, следует отнести его к классу рудных пегматитов или к классу безрудных.

Решающее правило будем строить исходя из стратегии Байеса. При равных априорных вероятностях гипотез P(H₁) = P(H₂) = 0,5 критическая точка х_k выбирается как абсцисса точки пересечения эмпирических кривых функции плотности распределения. Рис.1.3.5. Следовательно, если исследуемый образец характеризуется свойством х < x_k, его следует отнести к 1 классу, если х > x_k - ко второму.

При массовом распознавании мы будем совершать ошибки. Ошибка первого рода , а ошибка второго рода . Эти ошибки могут быть определены по графикам эмпирических функций распределения. В рассмотренном примере х_k = 13,3; .Общая ошибка диагностики

g = 0,5×0.13+0.5 × 0.24 = 0.185

Вопросы к четвёртой лабораторной работе.

1.В чём смысл работы?

2. В чём суть стратегии Байеса?

3. Дать определения ошибок первого и второго рода, написать формулы и показать на графике.

4. Написать формулы для критерия Котельникова и критерия максимального правдоподобия.

Лабораторная работа №5.

Вопросы к пятой лабораторной работе

1.В чём смысл работы?

2. Из какого предположения выполняем четвёртую лабораторную работу?

3. Написать формулу нормального закона распределения, построить его график.

4. Как выглядит Закон Гаусса (формула, график).

Лабораторная работа №6.

Проверка гипотезы о нормальном законе распределения.

Критерий Неймана –Пирсона

При изучении геологических процессов и явлений часто приходится проверять гипотезу о том, что выборка распределена по нормальному закону.

Будем пользоваться стратегией Неймана-Пирсона, суть которой состоит в том, что критическая точка определяется при заранее заданном уровне значимости 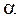. При этом минимизируется ошибка второго рода .

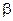В качестве критерия проверки гипотезы о нормальном законе распределения будем использовать критерий Пирсона или .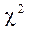

Будем сравнивать эмпирические частоты n_i , взятые из первой лабораторной работы и теоретические 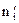частоты, вычисленные по формуле:

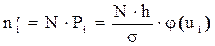(6.1)

Оценку расхождения между теоретической кривой нормального распределения и эмпирической кривой, полученной в результате опыта проводят, по величине отклонения .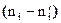

Задача формулируется так: при уровне значимости 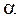требуется проверить нулевую гипотезу H_o о том, что генеральная совокупность распределена по нормальному закону.

Для проверки нулевой гипотезы о нормальном законе распределения рассмотрим случайную величину 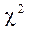, наблюдаемое значение которой вычисляются по формуле:

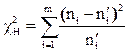(6.2)

Эта величина, как сумма квадратов нормально распределенных величин при 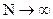, распределена по закону 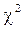с числом степеней свободы: k = m - r - 1,

где:

m- число интервалов группирования .

r- число параметров, определяющих закон распределения. (Для нормального закона r = 2)

Построим критическую область из условия заданной ошибки первого рода (уровень значимости) .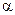

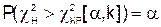
По таблице распределения c² приложение №5 (1) находим 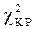и

при 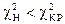делаем вывод о том, что нет оснований отвергать H_o;

при 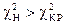- гипотезу H_o отвергаем.

Рассмотрим сквозной пример.

При решении задачи все расчеты запишем в таблицу.

Таблица 6.1

N	xi	ni	n'i=NPi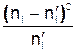
				0.33
			16,0	0.25
			12,0	0.33
				0.2
		N=50	N=50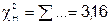

По заданному уровню значимости 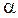=0,05 и числу степеней свободы k = 7-2-1=4 определяем критическое значение 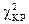. 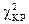= 9,5

Сравнивая 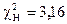c 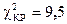делаем вывод:

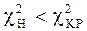, следовательно, нет оснований отвергать нулевую гипотезу H_o.

Таким образом, с надежностью 0.95 можно утверждать, что эмпирические данные не противоречат нормальному закону, т.е. имеющиеся расхождения носят случайный характер.

Вопросы к шестой лабораторной работе.

1.В чём смысл работы?

2. Написать критерий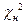

3. Почему, когда 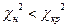– мы говорим нет, основания отвергать нулевую гипотезу?

4.В чём суть стратегии Неймана Пирсона?

5. Дать определение ошибки первого рода и написать формулу.

6. Пояснить смысл полученного результата в пятой лабораторной работе.

8. Можно ли с помощью критерия 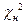проверить гипотезу о другом законе распределения?

Лабораторная работа №7.

Определение 7.3

Угловой коэффициент прямой линии регрессии

Y на X называют выборочным коэффициентом

регрессии Y на X и обозначают r .

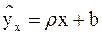( 7.1)

Будем пользоваться методом наименьших квадратов, суть которого состоит в том, что из всех возможных линий на плоскости (из всех возможных значений
r и b) нужно выбрать такие, сумма квадратов отклонений (ε_i)² , которых от линии регрессии была бы наименьшей.

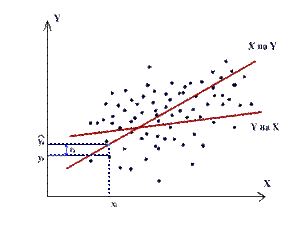
Рис.7.1

Из рисунка видно, что ε_i - отклонение наблюдаемого значения y_i от линии регрессии 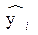. Наша задача – найти такое уравнение, чтобы 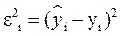( i =1,2,…N), было бы минимальным.

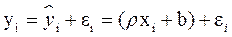
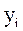–наблюдаемая ордината, соответствующая х_i

Уравнение регрессии Y на X имеет вид:

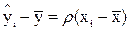
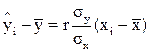(7. 2)

Аналогично запишем уравнение прямой линии регрессии X на Y: 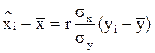(7.3)

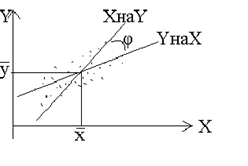Рис. 7..2

Выборочный коэффициент корреляции определяется равенством:

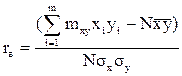(7. 4)

Коэффициент корреляции r изменяется от -1 до 1:

-1 £ r £ 1

Известно, что если величины X и Y независимы, то коэффициент корреляции r = 0; если r = ±1, то X и Y связаны линейной функцианальной зависимостью.

Cледовательно, коэффициент корреляции измеряет силу (тесноту) линейной связи между X и Y.

Выборочный коэффициент корреляции r_в является оценкой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами – количественными признаками X и Y.

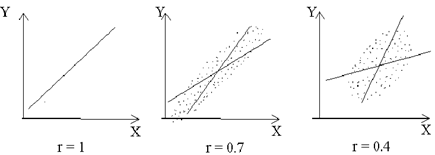
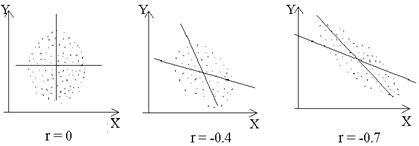
Рассмотрим различные примеры вида корреляционного облака и линий регрессии для некоторых значений r. Они приведены на следующих графиках:

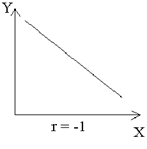Рис.7.3

Пример.

Дана выборка объёмом N = 34

Наши рекомендации

X	Y	X	Y
60.8	5.44	48.4	3.16
58.2	4.13	42.7	3.45
55.4	3.82	52.5	5.28
54.0	0.56	53.2	2.59
44.6	4.61	46.7	1.34
49.5	5.62	37.2	0.69
48.9	0.28	51.4	3.97
35.8	4.10	52.8	3.66
50.6	0.00	43.8	4.30
53.6	0.34	56.0	4.58
44.0	1.15	54.4	3.23