Тоді потрібні додаткові дослідження.

Алгоритмдослідження функції на екстремум

1. Знайти перші частинні похідні 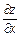та .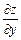

2. Знайти стаціонарні точки, тобто точки, в яких , .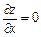

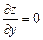3. Знайти частинні похідні другого порядку , , .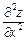

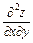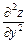4. Обчислити значення частинних похідних другого порядку в стаціонарних точках.

5. Для кожної стаціонарної точки знайти 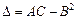і зробити висновки на базі теореми 11.

Приклад. Розглянемо функцію .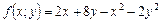

l 1. Знайдемо , .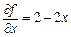

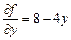2. Необхідна умова існування екстремуму полягає в тому, що 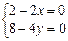. Розв’язком цієї системи є точка з координатами 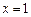, 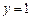. Таким чином, у точці (1; 2) функція може мати екстремум.

3. Знайдемо похідні другого порядку 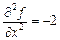, , 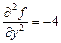, 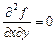звідки дістаємо, що .

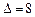4. Як випливає з пункту 5 алгоритму знаходження екстремуму — екстремум у точці (1; 2) існує. Це максимум, бо .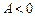

Приклад. Дослідити на екстремум функцію двох змінних:

.

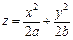
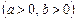l Знайдемо 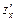і :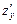

, .

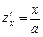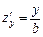2. Необхідна умова екстремуму: .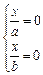

Отже, (0; 0) — стаціонарна точка.

3. Знайдемо , , :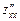

, , .

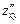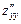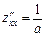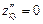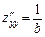4. У точці (0; 0)

, , .

.

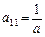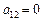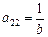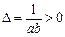5. Точка (0;0) — мінімум, хоча це ясно і безпосередньо.

9. Економічний зміст
частинних похідних

Аналогічно поняттю еластичності функції однієї змінної ми можемо ввести поняття частинних еластичностей функції двох змінних.

Припустимо, що функці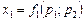ї і 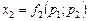виражають попит на товари 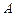і 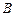, який залежить від ціни на ці товари. Частинні еластичності попиту відносно цін 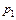і 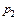подаються у вигляді:

, ,

, .

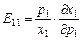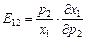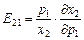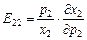Частинна еластичність 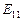попиту на товар 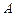відносно ціни товару 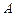приблизно означає відсоток підвищення (або зниження) попиту на товар 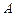, якщо ціна товару 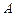зростає на 1%, а товару 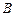залишається незмінною.

Частинна еластичність 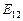попиту на товар 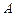відносно ціни товару 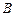приблизно означає відсоток підвищення (або зниження) попиту на товар 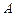, якщо ціна товару 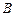зростає на 1%, а товару 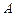залишається без змін, і т. ін.

Приклад. Припустимо, що функція попиту на товар 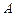є

.

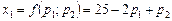Знайти частинні показники еластичностей.

l Маємо , .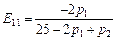

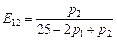Для 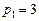, 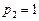дістаємо .

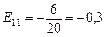Це означає, що коли ціна товару 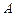зростає на 1%, а товару 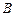залишається без змін, тоді попит на товар знижується на 0,3%. Далі, 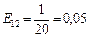, тобто якщо ціна товару 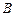зростає на 1% при незмінній ціні товару 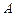, попит на товар 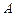зростає приблизно на 0,05%.

sКонтрольні запитання

1. Сформулюйте означення функції багатьох змінних.

2. Назвіть способи задання функцій багатьох змінних.

3. Що називають лініями рівня?

4. Сформулюйте означення функції двох змінних.

5. Сформулюйте теореми про границі суми, добутку та частки.

6. Сформулюйте означення неперервності функції в точці.

7. Сформулюйте означення неперервності функції в області.

8. Що називають повним приростом функції ?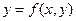

9. Що називають частинним приростом за ?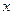

10. Що називають частинним приростом за ?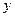

11. Яка функція називається диференційованою у точці ?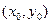

12. Що називають повним диференціалом функції?

13. Сформулюйте необхідну умову диференційованості функції в точці?

14. Як позначають похідні другого порядку?

15. Які точки називаються точками максимуму, мінімуму?

16. Сформулюйте необхідну умову екстремуму.

17. Сформулюйте достатню умову екстремуму.

18. Сформулюйте алгоритм дослідження функції на екстремум.

19. В чому полягає економічний зміст частинних похідних?