Оформление курсовой работы. Сборник заданий на курсовую работу по дисциплине

Федоров А.В.

Сборник заданий на курсовую работу по дисциплине

«Информатика»

Утверждено
на заседании кафедры

__________2009

Москва 2009

Оглавление

Список сокращений. 3

Общие требования. 4

Оформление курсовой работы.. 5

Вариант 1. Тень на орбите. 6

Вариант 2. Параметры орбиты.. 6

Вариант 3. Условие прямой видимости двух КА.. 7

Вариант 4. Трасса. 7

Вариант 5. Мгновенная зона радиовидимости. 8

Вариант 6. Мгновенная зона обзора аппаратурой КА.. 8

Вариант 7. Ширина полосы обзора. 9

Вариант 8. Расчет данных для планирования сеанса связи. 9

Вариант 9. Расчет данных целеуказания для НИП.. 10

Вариант 10. Расчет данных для планирования сеансов связи. 10

Вариант 11. Коррекция в плоскости орбиты КА.. 10

Вариант 12. Коррекция в плоскости орбиты КА.. 11

Вариант 13. Пространственная коррекция орбиты КА.. 11

Вариант 14. Коррекция орбиты боковым импульсом.. 11

Вариант 15. Коррекция орбиты боковым импульсом.. 12

Приложение. 13

1. Константы.. 13

2. Невозмущенное движение КА.. 13

3. Начальные условия. 16

4. Параметры орбиты.. 16

5. Положение и скорость КА в АГЭСК.. 18

6. Звездное время. 20

7. Положение КА в ГСК.. 20

8. Возмущенное движение КА порядка J₂₀ 21

9. Трасса КА.. 22

10. Направляющие косинусы Солнца. 22

11. Уравнение Кеплера. 23

12. Граница зоны облуживания на сферической Земле. 23

13. Когда НИП «видит» КА?. 24

14 Коррекция орбиты.. 25

Литература. 27

Список сокращений

АГЭСК	абсолютная геоцентрическая экваториальная система координат
ГСК	гринвичская система координат
НИП	наземный измерительный пункт
КА	космический аппарат
ИСЗ	искусственный спутник Земли
ППИ	пункт приема информации
ССО	солнечно-синхронная орбита

Общие требования

В каждом варианте задания на КР сформулирована задача проекта, способ решения которой следует найти, используя справочные материалы, приведенные в Приложении. Перед написанием исходного кода необходимо разработать концепцию программы, и ее структуру.

Проект Delphi курсовой работы обязательно должен содержать как минимум 1 прикладной модуль, с описанием констант, типов, переменных, процедур и функций, необходимых для решения задачи варианта КР.

Форма главного окна должна содержать компоненты пользовательского интерфейса для задания исходных данных и отображения результатов, а так же кнопку выполнения расчетов. Рекомендуется использовать стандартные компоненты палитры Standard:

Edit (TEdit) для ввода и редактирования исходных данных;

Label (TLabel), Memo (TMemo) – для отображения результатов расчетов.

Button (TButton) – кнопка выполнения расчетов.

Menu (TMenu) – главное меню программы.

Программа должна получать исходные данные из текстового файла, структуру которого предлагает и реализует программист. Рекомендуется использовать файл параметров, поддерживаемый объектом класса TIniFile. В части работы с исходными данными программа должна поддерживать общепринятые команды

Файл/Открыть

Файл/Создать

Файл/Сохранить

Файл/Сохранить как…

Результат работы программы (результаты расчетов) должны записываться в текстовый файл, формат которого был бы понятен таким приложениям Windows как NotePad (блокнот), GraphWin, MS EXcel и т.п.

В каждом варианте КР приводится задание на программирование в виде списка из трех пунктов, каждому из которых соответствует рейтинг, который получит студент в системе оценки знаний и навыков. Задачи составлены так, что получить рейтинг 3 можно лишь только выполнив требования всех пунктов задания.

Оценка КР

1) удовлетворительно (обязательный уровень) + зачет по курсу

2) хорошо

3) отлично

Не пытайтесь прибегать к услугам профессиональных программистов, т.к. «рука мастера» на фоне «новичка» видна невооруженным глазом.

Не следует убеждать преподавателя в том что «Я делал сам, но мне помогали…». Применительно к программированию это не проходит, ибо программа есть продукт интеллекта только ее автора, несмотря на то что формулы и алгоритмы выводят и придумывают другие люди.

Оформление курсовой работы

Пояснительная записка оформляется в соответствии с действующим стандартом.

Она должна содержать следующие разделы:

1. Задание на КР

2. Математическая модель

3. Алгоритм решения задачи

4. Структура проекта

5. Руководство пользователя

6. Список использованных источников

В первом разделе надо привести текст варианта задания.

Во втором разделе следует привести расчетные формулы, которые используются для получения требуемого результата.

В третьем разделе необходимо привести описание алгоритма решения задачи в виде блок-схемы. В блоках алгоритма необходимо ссылаться на элементы математической модели, которые используются, а не приводить формулы целиком.

В четвертом разделе приводится структура проекта – из каких модулей он состоит, какие функции выполняет тот или иной модуль. В этом разделе должны быть подразделы, содержащие:

– описание типов данных, сконструированных автором проекта;

– описание процедур и функций, созданных автором для реализации элементов математической модели;

– описание структур записей файлов исходных данных и результатов.

В пятом разделе необходимо дать краткое описание программы:

– для чего она предназначена (какую прикладную задачу или группу задач можно решить с ее помощью)

– пользовательский интерфейс: главное меню, окна ввода исходных данных, какие кнопки для чего предназначены

– описание формата представления исходных данных в текстовом файле

– описание формата представления результатов расчетов в текстовом файле.

В список использованных источников включите позиции списка литературы, приведенного в данном сборнике заданий, а также то, что Вы нашли самостоятельно (например, в Интернете) и использовали при выполнении курсовой работы.

Вариант 1. Тень на орбите

Условие освещенности космического аппарата (КА) на орбите в случае цилиндрической модели тени можно определить, вычислив угол между вектором положения КА 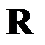и единичным вектором Солнца 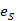. Оба вектора должны быть в одной системе координат, например, в АГЭСК.

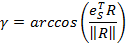
КА освещен Солнцем либо если g£p/2, либо при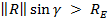

где 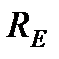– средний радиус Земли.

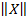– норма вектора,

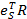– скалярное произведение векторов.

Исходные данные: – стандартные начальные условия.

Задача.

1) Определить, освещен КА Солнцем или нет в начальный момент времени.

2) Определить освещенность в заданный момент времени на текущем витке.

3) Определить длительность теневого участка на текущем витке.

Текущий виток начинается от момента начальных условий. Его длительность равна периоду обращения КА

Вариант 2. Параметры орбиты

Исходные данные: – стандартные начальные условия.

Задача.

1) Для заданных начальных условий вычислить параметры орбиты.

2) Вычислить параметры орбиты в заданный момент времени на текущем витке

3) На текущем витке определить длительность участка, на котором высота КА над землей среднего радиуса больше высоты, заданной пользователем.

Текущий виток начинается от момента начальных условий. Его длительность равна периоду обращения КА

Вариант 3. Условие прямой видимости двух КА

Условие прямой видимости двух КА, обращающихся по орбитам вокруг Земли имеет вид

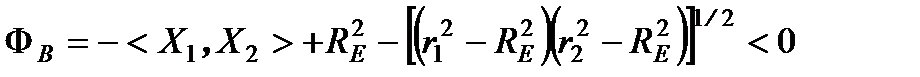
где <a,b> – скалярное произведение векторов;

X_k – вектор положения k-го КА в АГЭСК

R_E – средний радиус Земли

r_k – модуль вектора Х_k.

Исходные данные: КА₁– стандартные начальные условия. КА₂– геостационарный спутник, точка стояния которого задана геоцентрической долготой в диапазоне 0¸360⁰.

Задача.

1) Для заданных начальных условий вычислить условие видимости.

2) Вычислить условие видимости в заданный момент времени на текущем витке

3) На текущем витке определить длительность участка, на котором КА находятся в прямой видимости

Текущий виток начинается от момента начальных условий. Его длительность равна периоду обращения КА

Вариант 4. Трасса

Исходные данные: – стандартные начальные условия.

Задача.

1) Для заданных начальных условий вычислить географические координаты КА

2) Вычислить географические координаты КА заданный момент времени на текущем витке.

3) Вычислить координаты точек трассы текущего витка с заданным шагом по времени с записью в файл таблицы < время- аргумент широты долгота-широта> .

Вариант 5. Зона видимости КА

Центральный угловой радиус зоны видимости КА из пункта слежения определяют по формуле

,

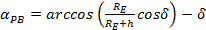где

d – минимальный угол места, характерный для местности, над которой пролетает КА,

h – высота КА в точке расчета:

R_E – средний радиус Земли.

Исходные данные: – стандартные начальные условия и угол d, шаг расчета границы по азимуту DА

Задача.

1) Для заданных начальных условий вычислить координаты точек границы зоны радиовидимости с заданным шагом по азимуту с записью в текстовый файл в виде таблицы <Азимут- долгота – широта> и изображением ЗРВ на карте.

2) Рассчитать координаты точек границы зоны радиовидимости с заданным шагом по азимуту в заданный момент времени на текущем витке с записью в текстовый файл в виде таблицы <Азимут- долгота – широта>..

3) Найти точки на трассе, в которых угловой радиус зоны минимальный и максимальный. (примечание: в случае круговой орбиты данная задача теряет смысл).

Вариант 6. Мгновенная зона покрытия аппаратурой КА

Центральный угловой радиус зоны покрытия Земли аппаратурой КА вычисляют по формуле

,

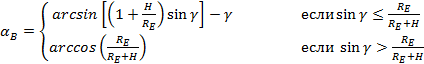где g – угловой радиус поля зрения аппаратуры,

H – высота КА в точке расчета:

R_E – средний радиус Земли.

.

Исходные данные: – стандартные начальные условия и угол g, шаг расчета границы по азимуту DА

Задача.

1) Для заданных начальных условий вычислить координаты точек границы зоны обзора с заданным шагом по азимуту с записью в текстовый файл в виде таблицы <Азимут- долгота – широта> и изображением ЗО на карте.

2) Рассчитать координаты точек границы зоны обзора с заданным шагом по азимуту в заданный момент времени на текущем витке с записью в текстовый файл в виде таблицы <Азимут- долгота – широта>.

3) Найти точки на трассе, в которых угловой радиус зоны минимальный и максимальный. (примечание: в случае круговой орбиты данная задача теряет смысл).

Вариант 7. Ширина полосы обзора

В своем движении относительно Земли аппаратура наблюдения «освещает» на поверхности Земли полосу, линейный размер которой равен

,

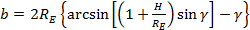где R_e– средний радиус Земли;

h – высота КА над Землей;

g– центральный радиус поля зрения аппаратуры КА.

Исходные данные: – стандартные начальные условия, угол g

Задача.

1) Для заданных начальных условий вычислить ширину полосы обзора.

2) Рассчитать ширину полосы обзора в заданный момент времени на текущем витке с записью в текстовый файл в виде таблицы <время- ширина>.

3) Найти точки на трассе, в которых ширина полосы обзора минимальна и максимальна. (примечание: в случае круговой орбиты данная задача теряет смысл).

Вариант 8. Расчет данных для планирования сеанса связи

Для планирования сеанса связи КА-НИП необходимо найти время входа в зону данного НИП, время покидания зоны, минимальный угол КА-Солнце (если сеанс приходится на освещенный участок орбиты) и длительность контакта. Чтобы обеспечить слежение антенны НИП за КА нужна таблица азимутов и углов места КА по времени от момента входа до момента выхода из зоны.

Исходные данные: – стандартные начальные условия, координаты НИП и минимальный угол места НИП.

Задача.

1) Вычислить длительность контакта на текущем витке, а также время, азимут и угол места КА в точках входа и выхода в зону НИП.

2) Вычислить минимальное значение угла КА-Солнце в окне сеанса (если сеанс приходится на дневное время)

3) Вычислить общее время контакта для сети из нескольких НИП на текущем витке (количество НИП, координаты и минимальные углы места для каждого НИП задаются в составе исходных данных.

Вариант 9. Расчет данных целеуказания для НИП

Данные целеуказания необходимы для задания программы разворота антенны НИП на КА перед началом сеанса и слежения за КА в течение его прохождения зоны данного НИП. Для слежения за КА нужна таблица азимутов и углов места КА по времени от момента входа до момента выхода из зоны.

Исходные данные: – стандартные начальные условия, координаты НИП и минимальный угол места НИП.

Задача.

1) Определить моменты начала и окончания контакта КА-НИП и составить таблицу <время – место – азимут> в окне сеанса на текущем витке.

2) Определить, будет ли момент когда антенну надо будет направить в зенит?

3) Определить, будет ли момент засветки антенны Солнцем?

Вариант 10. Расчет данных для планирования сеансов связи

Для планирования сеанса связи КА-НИП необходимо найти время входа в зону данного НИП, время покидания зоны, минимальный угол КА-Солнце (если сеанс приходится на освещенный участок орбиты) и длительность контакта. Чтобы обеспечить слежение антенны НИП за КА нужна таблица азимутов и углов места КА по времени от момента входа до момента выхода из зоны.

Исходные данные: – стандартные начальные условия, координаты и минимальные углы места двух НИП.

Задача.

1) Вычислить моменты начала и окончания окна контакта каждого НИП.

2) Вычисть суммарное время контакта на текущем витке

3) Вычислить общее время контакта, приходящееся на освещенный участок орбиты.

Вариант 11. Коррекция в плоскости орбиты КА

Исходные данные: – стандартные начальные условия, приращения скорости ΔV_X и ΔV_Y , выраженные в м/с.

Задача

1) Вычислить приращения Da, Dе и Dw при коррекции в начальный момента времени.

2) Вычислить приращения Da, Dе и Dw при коррекции в заданный момент времени на текущем витке.

3) Вычислить приращения Da, Dе и Dw если коррекция проводится в момент прохождения перигея или апогея орбиты ( попутно получить и вывести соответствующий момент времени)

Вариант 12. Коррекция в плоскости орбиты КА

Исходные данные: – стандартные начальные условия, приращения скорости ΔV_X и ΔV_Y , выраженные в м/с.

Задача

1) Вычислить новые параметры при коррекции орбиты в начальный момент времени.

2) Вычислить новые параметры при коррекции в заданный момент времени на текущем витке

3) Вычислить новые параметры при коррекции орбиты в момент прохождения перигея или апогея орбиты (попутно получить и вывести соответствующий момент времени).

Вариант 13. Пространственная коррекция орбиты КА

Исходные данные: – стандартные начальные условия, приращение скорости ΔV и углы Эйлера, задающие ориентацию КА относительно осей орбитальной системы координат

Задача

1) Вычислить новые параметры при коррекции орбиты в начальный момент времени.

2) Вычислить новые параметры при коррекции в заданный момент времени на текущем витке

3) Вычислить новые параметры при коррекции орбиты в момент прохождения перигея или апогея орбиты (попутно получить и вывести соответствующий момент времени).

Вариант 14. Коррекция орбиты боковым импульсом

Прикладывается только боковой импульс ΔV_Z

Исходные данные: – стандартные начальные условия, приращение скорости ΔV_Z , выраженное в м/с.

Задача

1) Вычислить новые параметры орбиты при коррекции орбиты в начальный момент времени.

2) Вычислить новые параметры при коррекции в заданный момент времени на текущем витке

3) Вычислить новые параметры при коррекции орбиты в момент прохождения восходящего или нисходящего узла орбиты (попутно получить и вывести соответствующий момент времени).

Вариант 15. Коррекция орбиты боковым импульсом

Прикладывается только боковой импульс ΔV_Z

Исходные данные: – стандартные начальные условия, приращение скорости ΔV_Z , выраженное в м/с.

Задача

4) Вычислить новые параметры орбиты при коррекции орбиты в начальный момент времени.

5) Вычислить новые параметры при коррекции в заданный момент времени на текущем витке

6) Вычислить новые параметры при коррекции орбиты в момент верхней или нижней кульминации (аргумент широты равен 90^О или 270^О. ( попутно получить и вывести соответствующий момент времени).

Приложение

Константы

RЕ	средний радиус Земли	6371.21	км
e	угол наклона плоскости экватора Земли к эклиптике	23027’08”.26
m	гравитационная постоянная Земли	0.398603106	км3/с2
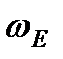	угловая скорость суточного вращения Земли	0.729211510-4	с-1
C20	коэффициент второй зональной гармоники	1.082627e-3	-
TS	средние звездные сутки	86164.03	с
ТС	средние солнечные сутки		с
ALS	астрономическая единица в световых секундах	499.00478353	с
VL	скорость света	299792.458	км/с

JD2K15	юлианская дата эпохи 2000 г., январь 1.5. (1 января 12 час)	2451545.0
JC	число дней в юлианском столетии

Невозмущенное движение КА

Невозмущенное движение КА подчиняется трем законам Кеплера, из которых следует, что форма орбиты — это сечение конуса плоскостью, определяющее эллипс, параболу или гиперболу.

Замкнутая орбита представляет собой эллипс, в одном из фокусов которого находится Земля.

В полярной системе координат уравнение конического сечения имеет вид

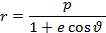
где r – расстояние от фокуса до КА (т.н. радиус-вектор КА);

J – полярный угол (т.н. истинная аномалия), который отсчитывается от момента прохождения перицентра;

р – фокальный параметр ;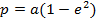

е – эксцентриситет, 0£е<1;

a – большая полуось орбиты (эллипса);

Размер большой полуоси орбиты вытекает из первого закона Кеплера и вычисляется по формуле

,

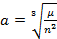где 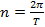– среднее движение или средняя угловая скорость радиус-вектора r,

Т – период обращения,

µ – гравитационная постоянная Земли.

Перицентром (перигеем) орбиты называется точка наименьшего удаления КА от фокуса на расстояние:

,

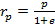Апоцентром (апогеем) орбиты называется точка наибольшего удаления КА от фокуса на расстояние

,

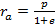Линия между перицентром и апоцентром называется линией апсид.

Положение перицентра орбиты задается углом w, который называется аргументом перицентра. Он отсчитывается в направлении движения КА от восходящего узла орбиты.

Восходящий узел орбиты это точка, в которой КА переходит из южного полушария Земли в северное. Противоположный узел называют нисходящим. Линия, лежащая в плоскости экватора между узлами, называется линией узлов.

Ориентация плоскости орбиты в пространстве определяется углами наклона плоскости к экватору i и долготой восходящего узла W. Долгота восходящего узла отсчитывается от направления на точку весеннего равноденствия, в которой Земля в движении вокруг Солнца переходит из южного его полушария в северное.

При невозмущенном движении все определяющие параметры орбиты ( a, e, w_p, i, W) постоянны. Переменными по времени являются истинная аномалия, радиус-вектор, а также скорость движения КА по орбите.

Истинная аномалия связана со временем движения уравнением Кеплера.

,

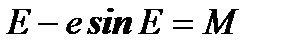где М – вспомогательный угол, отсчитываемый от перигея, который называется средней аномалией КА. Это угол, на который повернется радиус-вектор если бы КА двигался по круговой орбите с тем же периодом обращения что и по эллиптической. Средняя аномалия вычисляется по формуле

,

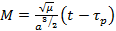где

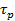– время прохождения перигея орбиты (с),

t – текущий момент времени (с).

Неизвестной величиной является угол Е – эксцентрическая аномалия.

Уравнение Кеплера решают методом последовательных приближений по схеме

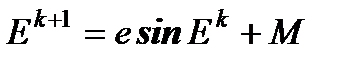, k=0,1,…

при начальном приближении Е⁰ =М.

Решение уравнения заканчивают при выполнении условия

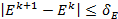
где d_E – точность решения.

Истинная аномалия однозначно связана с эксцентрической аномалией уравнением

,

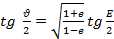Часто для расчетов положения КА относительно Земли удобно использовать вспомогательную угловую величину – аргумент широты КА. Это угол u, который отсчитывается в плоскости орбиты от восходящего узла до КА в направлении его движения по орбите. По этому углу определяют географическую широту точки земной поверхности, над которой находится КА, и поэтому он так и назван:

.

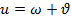Для расчета положения КА на орбите в любой момент времени в полярной системе координат (r,J) обычно задают начальные условия – определяющие параметры, отнесенные к моменту прохождения восходящего узла.

Для расчета положения КА на орбите в любой момент времени необходимо найти момент прохождения перигея . С использованием вышеприведенных формул найдем что

,

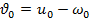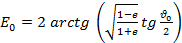
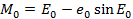
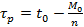
Начальные условия

В качестве исходных данных, определяющих форму орбиты, положение ее плоскости в пространстве и положение КА в заданный момент времени будем задавать следующие начальные условия:

R_p – минимальное расстояние от центра Земли до КА в перицентре (км),

e – эксцентриситет орбиты (0£e<1)

u – аргумент широты (угол от восходящего узла до радиус-вектора КА) (град),

w – аргумент перицентра – угол от восходящего узла до перигея (град),

W – долгота восходящего узла (град),

i – наклонение плоскости орбиты к плоскости экватора Земли (град).

Начальные условия всегда привязаны к моменту времени t₀, на который они получены решением навигационной задачи обработки траекторных измерений. Этот момент может быть задан произвольно. Важно то что все дальнейшие вычисления, связанные с моделированием движения КА по времени проводятся от момента t₀.

Начальный момент времени задается датой и временем суток в дате (переменная типа TDateTime).

Параметры орбиты

По исходным данным можно рассчитать значения следующих параметров орбиты:

Истинная аномалия ,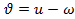

Радиус перицентра 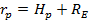где R_E – средний радиус Земли,

Фокальный параметр ,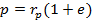

Расстояние от начала координат до КА ,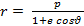

Большая полуось орбиты (эллипса) ,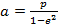

Малая полуось орбиты (эллипса) ,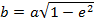

Период обращения ,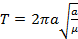

Средняя угловая скорость радиус-вектора (среднее движение) ,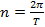

Угловая скорость радиус-вектора ,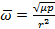

Орбитальная скорость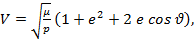

Скорость в апоцентре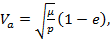

Скорость в перицентре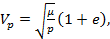

Скорость вдоль нормали к радиус-вектору (трансверсальная)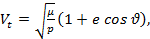

Скорость вдоль радиус-вектора (радиальная).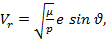

Эксцентрическая аномалия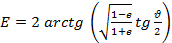

Средняя аномалия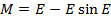

Момент времени прохождения перигея ,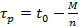

Угол между радиус-вектором и вектором орбитальной скорости

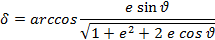
Драконический период обращения – время движения КА на интервале аргумента широты от 0 до 2p (от одного восходящего узла до другого) по незамкнутой возмущенной орбите

,

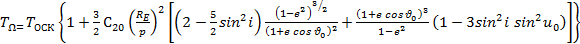где T_оск – оскулирующий период обращения (см. ниже).

Аномалистический период обращения – время движения на интервале [0..2p] аргумента J по незамкнутой возмущенной орбите

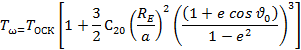
Среднее возмущенное движение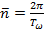

Оскулирующий период обращения