Если воспользоваться выражением для косинуса двойного аргумента

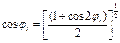
тогда мгновенное локальное значение фактора косинуса для данного i-го гелиостата в данный момент времени есть косинус половины угла между векторам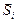и и .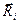

Значения фактора косинуса cosj является коэффициентом эффективности использования гелиостатов h для оптической системы солнечной электростанции.

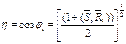
17. Расчетная методика для определения на любой глубине температура горных пород ( )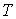

ОТВЕТ

Повышение температуры Земли с углублением на единицу длины называется геотермическим градиентом.

Величина, соответствующая углублению в метрах, при котором температура повышается на 1° С, называется геотермической ступенью.

В связи с изменением интенсивности солнечного излучения, тепловой режим первых 1,5-40 м земной коры характеризуется суточными и годовыми колебаниями. Далее имеют место многолетние и вековые колебания температуры, которые с глубиной постепенно затухают.

На любой глубине температура горных пород ( 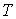) приближенно может быть определена по формуле:

,

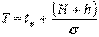где 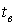-средняя температура воздуха данной местности; 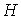-глубина, для которой определяется температура; 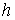-глубина слоя постоянных годовых температур; 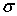-геотермическая ступень.

Средняя величина геотермической ступени равна 33 м, и с углублением от зоны постоянной температуры на каждые 33 м температура повышается на 1°С. Геотермические условия чрезвычайно разнообразны. Это связано с геологическим строением того или иного района Земли. Известны случаи, когда увеличение температуры на 1°С происходит при углублении на 2-3 м. Эти аномалии обычно находятся в областях современного вулканизма.На глубине 400-600 м в некоторых районах, например, Камчатки, температура доходит до 150-200 °С и более.Значение геотермических градиента и степени для разных частей земного шара разные. Наибольший геотермический градиент, который равен 150 °С/км, зафиксирован в Бананце (штат Орегон, США). Ему соответствует геотермическая степень, которая равна 6,6 м/°С. Это зона молодой вулканической активности.

Расчетная методика для определенияпреобразования энергии волнОгромные количества энергии можно получить от морских волн. Мощность, переносимая волнами на глубокой воде, пропорциональна квадрату их амплитуды и периоду. Поэтому наибольший интерес представляют длиннопериодные ( 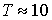с) волны большой амплитуды ( 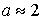м), позволяющие снимать с единицы длины гребня в среднем от 50 до 70 кВт/м.

Наибольшее число волновых энергетических устройств разрабатывается для извлечения энергии из волн на глубокой воде. Это наиболее общий тип волн, существующий при условии, что средняя глубина моря 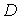превышает величину половины длины волны .

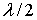В волнах на глубокой воде нет поступательного движения жидкости. В подповерхностном слое жидкости ее частицы совершают круговое движение с радиусом орбиты 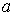, равным амплитуде волны.

Высота волны 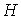от вершины гребня до основания равна ее удвоенной амплитуде ( 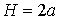). Угловая скорость движения частиц 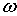измеряется в радианах в секунду. Изменение формы волновой поверхности таково, что наблюдается поступательное движение, хотя сама вода не перемещается в направлении распространения волны (слева направо). Это кажущееся перемещение есть результат наблюдения фаз смещения последовательно расположенных частиц жидкости; как только одна частица в гребне опускается, другая занимает ее место, обеспечивая сохранение формы гребня и распространение волнового движения вперед.

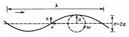
. Характеристики волны

Соотношение, устанавливающее зависимость между частотой и длиной для поверхностной волны на глубокой воде

.

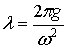Период движения волны

.

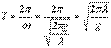Скорость частицы жидкости в гребне волны

.

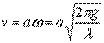Скорость перемещения поверхности волны в направлении 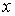определится как

.

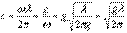Скорость 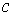называют фазовой скоростью распространения волн, создаваемых на поверхности жидкости. Эта величина не зависит от амплитуды волны и неявным образом связана со скоростью движения частиц жидкости в волне.

Полная кинетическая энергия на единицу ширины волнового фронта и единицу длины вдоль направления распространения волны равна

.

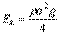Нормированная потенциальная энергия волны равна в точности такой же величине

.

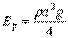Полная энергия на единицу площади поверхности волны равна сумме кинетической и потенциальной энергий.

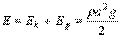. 14.7)

Расчетная методика для определениямощностивыработки энергии ветроустановокОтносительные аэродинамические характеристики удобны для предварительного проектирования ветрогенераторов.Наиболее важной характеристикой является коэффициент использования энергии ветра - x.Это отношение мощности вращательного движения ротора к мощности ветрового потока, протекающего через ометаемую ротором поверхность. В номинальном режиме для быстроходных ветрогенераторов достигается максимум x_мах = 0,4-0,5.Ограничение мощности ротора объясняет закон Бетца, впервые сформулированный немецким физиком Альбертом Бетцем в 1919 году. Этот закон поясняет, что, чем больше энергии может забрать турбина у ветрового потока, тем меньше будет скорость ветра после турбины.Это значительно снижает потенциально возможную выработку турбины. На основе закона Бетца можно подсчитать, что идеальная ветротурбина может преобразовать в механическую энергию только 59% кинетической энергии ветрового потока.Мощность ветрогенератора можно определить следующим образом:

N = x p R² 1/2 r V³ h_редh_ген,

где R – радиус ротора, r - плотность воздуха (1,25кг/м³), V – скорость ветра, h_ред – КПД редуктора (0,9-0,95), h_ген – КПД генератора – (0,7-0,9).