Критерий Фишера (Сравнение дисперсий двух нормальных генеральных совокупностей).
Описание
В качестве критериальной статистики для проверки гипотезы о равенстве генеральных дисперсий нормально распределенных генеральных совокупностей используют отношение выборочных дисперсий, т. е. случайную величину:
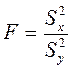
где 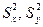 – исправленные выборочные дисперсии для выборок объемом
– исправленные выборочные дисперсии для выборок объемом 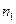 и
и 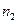 соответственно.В качестве нулевой гипотезы H0 формулируется гипотеза о равенстве генеральных дисперсий.
соответственно.В качестве нулевой гипотезы H0 формулируется гипотеза о равенстве генеральных дисперсий.
Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера-Снедекора со степенями свободы 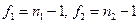 . Одной из функций, осуществляющей проверку данного критерия в R является var.test()
. Одной из функций, осуществляющей проверку данного критерия в R является var.test()
Описание функции
var.test(x,y,alternative = c("two.sided", "less","greater"), conf.level = 0.95, ...)
Параметры
| x,y | вектор или объекты линейной модели (например, класса lm). |
| conf.level | доверительная вероятность |
| Alternative | альтернативная гипотеза. Может быть одна из "two.sided" (по умолчанию)-двустороняя критическая область, "greater" -правостороняя критическая область или "less"-левостороняя критическая область. |
Пример
> x<-c(3.5, 3.6, 7.8, 9.6, 5.7, 8.9, 6.3)
> y<-c(1.0, 2.7, 8.9, 6.5, 8.9, 6.5,12.5,10.2, 1.2)
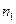 =7,
=7, 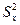 =5.86;
=5.86; 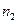 =9,
=9, 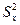 =16.75
=16.75
> var.test(x, y, alternative = c("two.sided"), conf.level = 0.95)
F test to compare two variances
data: x and y
F = 0.3498, num df = 6, denom df = 8, p-value = 0.2174
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.07519108 1.95855792
Результат теста:
F = 0.3498 ( значение F статистики), число степеней свободы для х - 6, для y - 8
p-value = 0.2174, т.е. уровень ошибки, при котором можно отвергнуть гипотезу о равенстве дисперсий, равен 21.74%
95% доверительный интервал: (0.075, 1.959) - полученное нами значение F-статистики в него попадает, следовательно гипотеза о равенстве дисперсий принимается на 5% уровне значимости.
Критерий Стьюдента (Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы).
Описание
Если предположить, что неизвестные генеральные дисперсии равны между собой, то для решения этой задачи можно применить критерий Стьюдента. Т.е. нужно, пользуясь критерием Фишера, предварительно проверить гипотезу о равенстве генеральных дисперсий. В случае независимых выборок в качестве критериальной статистики для проверки гипотезы принимают случайную величину:
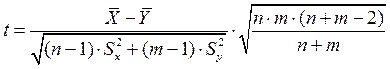 ,
,
где 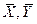 - выборочные средние,
- выборочные средние, 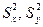 – выборочные дисперсии,
– выборочные дисперсии, 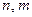 – объемы выборки и
– объемы выборки и 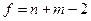 - число степеней свободы для распределения критериальной статистики (если дисперсии не равны, то критерий остается применимым, но требует коррекции приводенной формулы и числа степеней свободы – необходимость такой коррекции указывается при вызове функции). Если выборки зависимые (парная выборка), то проверяется гипотеза о равенстве матожидания нулю для новой случайной величины
- число степеней свободы для распределения критериальной статистики (если дисперсии не равны, то критерий остается применимым, но требует коррекции приводенной формулы и числа степеней свободы – необходимость такой коррекции указывается при вызове функции). Если выборки зависимые (парная выборка), то проверяется гипотеза о равенстве матожидания нулю для новой случайной величины 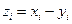 , также имеющей нормальное распределение. В этом случае используется критериальная статистика Стьюдента
, также имеющей нормальное распределение. В этом случае используется критериальная статистика Стьюдента
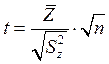
Одной из функций, осуществляющей проверку данного критерия в R является t.test()
Описание функции
t.test (x, y = NULL, alternative = c ("two.sided", "less", "greater"), var.equal = FALSE, conf.level = 0.95, paired = FALSE,...)
Параметры
| x | Числовой вектор значений. |
| y | Числовой вектор значений (используется для парного теста, см. ниже). |
| paired | Признак парного теста: проверяется гипотеза для x-y, поэтому вектор y должен присутствовать и соответствовать по длине вектору x. |
| alternative | Символьная строка, определяющая альтернативную гипотезу, должна быть одна из "two.sided" (по умолчанию)-двустороняя критическая область, "greater" -правостороняя критическая область или "less"-левостороняя критическая область. |
| var.equal | Логическая переменная, указывающая на равенство дисперсий |
| conf.level | Доверительная вероятность. |
Примечание
По умолчанию var.equal=FALSE (дисперсии предполагаются неравными), в этом случае для вычислений используется оценка Велча (Welch).
