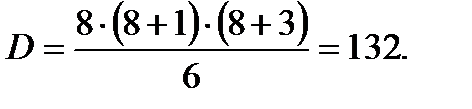Оценка точности удаленной стороны сплошной сети триангуляции 4 класса
Имеем ряд треугольников (рисунок 9). Углы в треугольниках измерены независимо друг от друга и уравнивание ряда выполняется по углам. Вес всех измеренных углов одинаков и равен единице.
А1=68°, А2=72°, А3=52°;
В1=44°, В2=55°
| С3 |
| В3 |
| С1 |
С1=
| С2 |
Среднюю квадратическую погрешность логарифма для наиболее удаленной стороны (Равнинный-Теклинский) определяем по формуле:
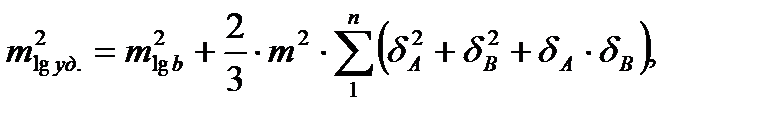
где m = 2" – средняя квадратическая ошибка измерения углов;
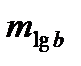 – ошибка логарифма выходной стороны;
– ошибка логарифма выходной стороны;
δ – изменение функции lg sin на 1'.
Ошибку логарифма выходной стороны определяем по формуле:
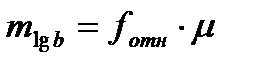 ,
,
где 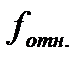 – относительная ошибка выходной стороны;
– относительная ошибка выходной стороны;
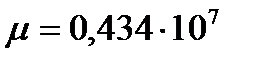 .
.
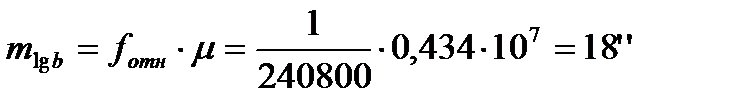 .
.
Для определения средней квадратической ошибки логарифма удаленной стороны определяем углы A,B,C в треугольниках (рисунок 9).
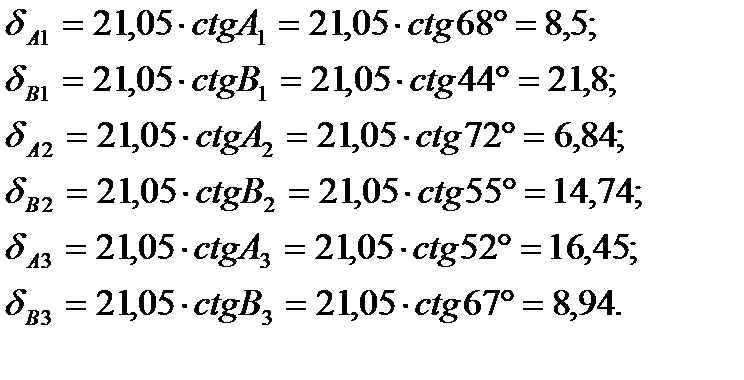
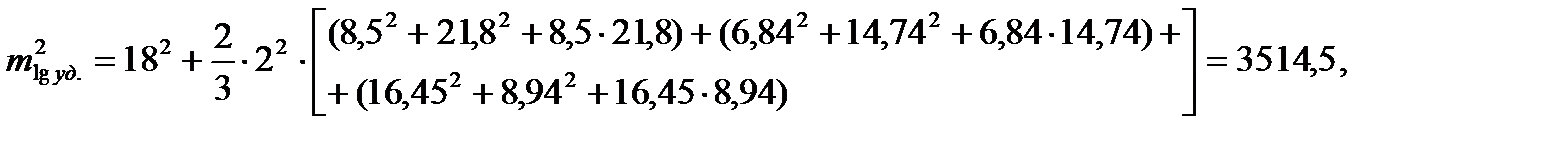
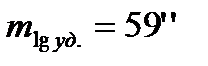 .
.
Относительная ошибка удаленной стороны вычисляется по формуле:
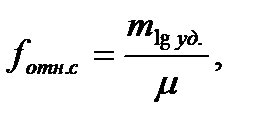
где 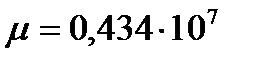 ;
;
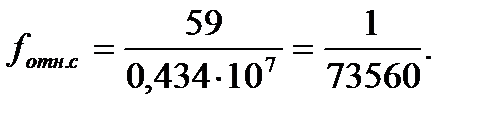
Полученную относительную ошибку удаленной стороны сравниваем с допустимой относительной ошибкой 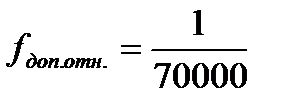 и делаем вывод о том, что относительная ошибка удаленной стороны удовлетворяет требуемым условиям «Инструкции…».
и делаем вывод о том, что относительная ошибка удаленной стороны удовлетворяет требуемым условиям «Инструкции…».
Ошибка дирекционного угла наиболее удаленной стороны сети
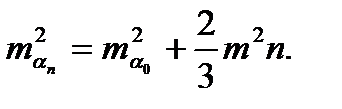
Среднюю квадратическую ошибку дирекционного угла исходной стороны 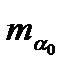 принимаем равной ± 3, а угла сети – m=±2".
принимаем равной ± 3, а угла сети – m=±2".
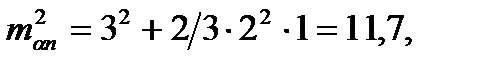
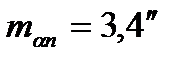 .
.
Погрешность в координатах х, у пунктов триангуляционной сети в районе строительства рудника
Вычисляем по формуле:
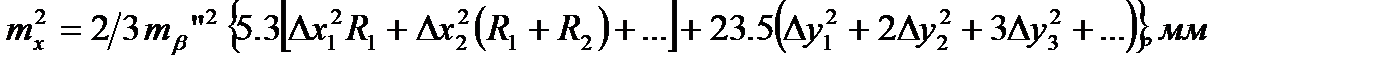 ;
;
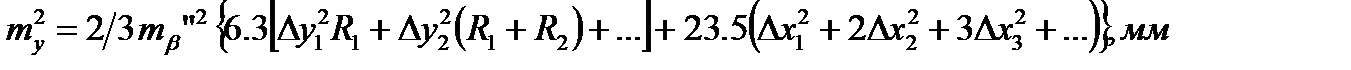 ;
;
где 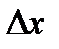 и
и 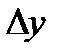 - приращение координат связующих сторон треугольников, определяемых с проекта триангуляции с помощью компьютерной графики (рисунок 10), км;
- приращение координат связующих сторон треугольников, определяемых с проекта триангуляции с помощью компьютерной графики (рисунок 10), км;
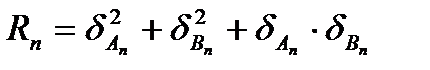 – определяем для каждого треугольника по связующим углам А и В;
– определяем для каждого треугольника по связующим углам А и В;
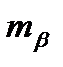 – средняя квадратическая ошибка измеренных углов в триангуляции 4 класса, принимается равной ± 2;
– средняя квадратическая ошибка измеренных углов в триангуляции 4 класса, принимается равной ± 2;
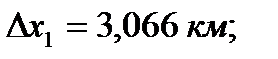
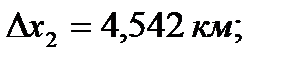
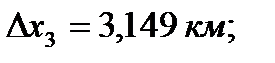
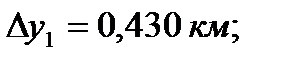
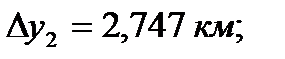
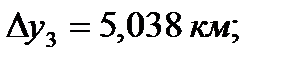
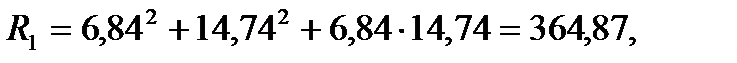
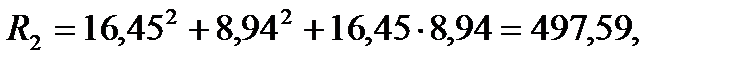
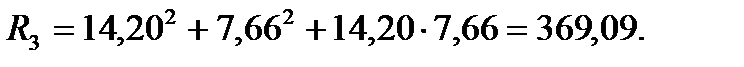
Для пункта Теклинский:
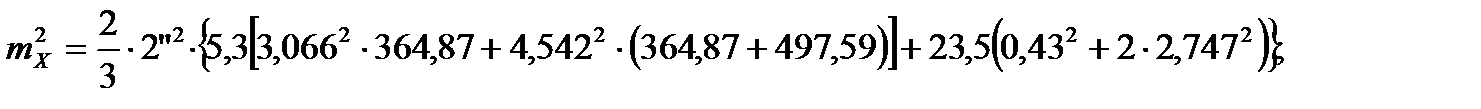
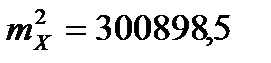 ;
;
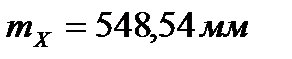 ;
;
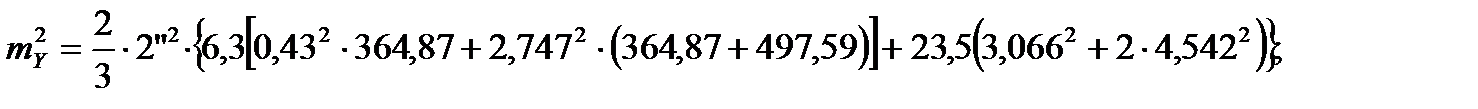
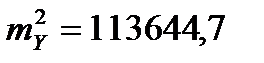 ;
;
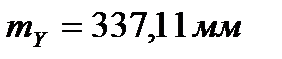 .
.
Для пункта Высотный:
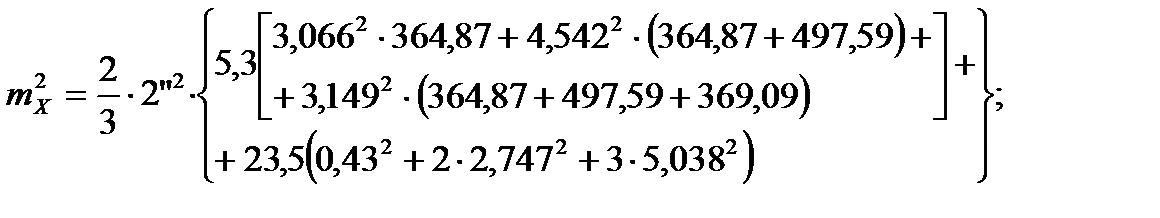
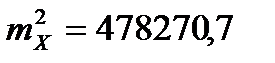 ;
;
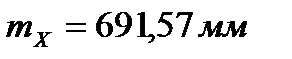 ;
;
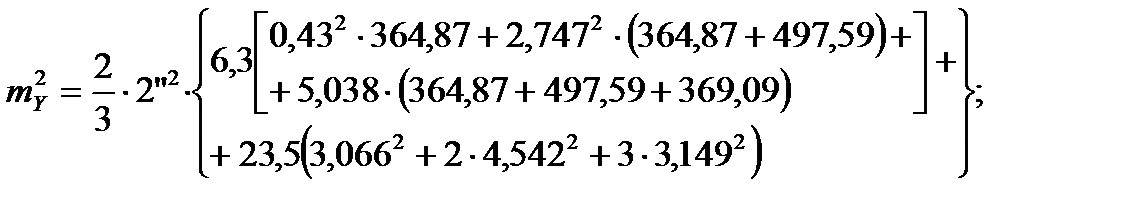
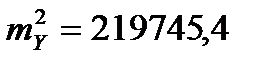 ;
;
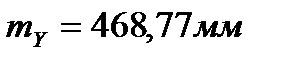 .
.
2.7.Определение числа условных уравнений, возникающих в
запроектированной сети
Составляем условные уравнения и разбиваем их на две группы.
Число всех уравнений определяем по формуле:
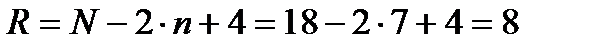 .
.
Число уравнений полюса подсчитываем по формуле:
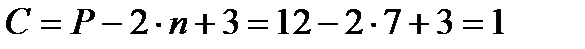 .
.
Число уравнений фигур находим по выражению:
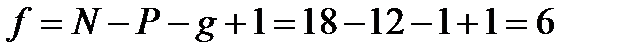
где N – число измеренных углов в сети;
п – число всех точек в сети;
Р – число всех линий в сети (сплошных и не сплошных);
g – число центральных точек сети, на которых измерены все углы.
Уравнения фигур:
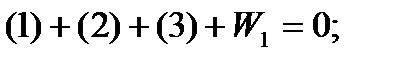
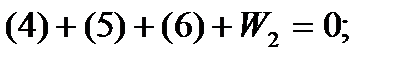
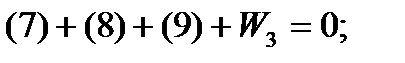
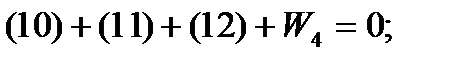
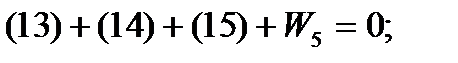
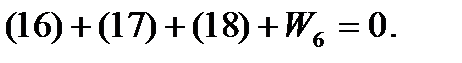
Уравнение горизонта:
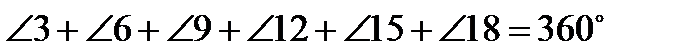 .
.
Уравнение полюса:
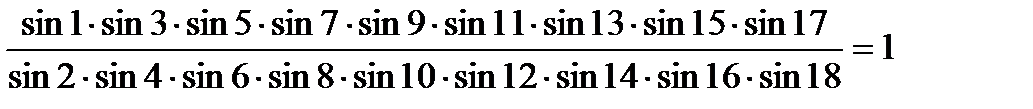 .
.
Подсчет математических действий для решения нормальных уравнений
Выполняем по формуле:
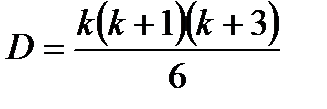 ;
;
где D – число арифметических действий при решении нормальных уравнений;
k – число условных или нормальных уравнений, возникающих в сети.