Контрольная работа по математической логике. Староста одного класса дал следующие сведения об учениках: «В классе учатся 40 школьников, в том числе 22 девочки
Вариант 8
Задание №1.
Даны множества А={-10,-9,-8,-7,-6,-5,-4,-3,-2,0); В={-13,-11,-8,-6,-4,-2,-1,0,1,2,}; С={-12,-9,-7, -6,-5, -3,-1, 0, 1, 3}. Задайте множества: а) (АÈВ)ÇС; б) АÇВÇС; в) (АÇС)\B; г)(A\B) Ç (C\B).
Задание №2.
Староста одного класса дал следующие сведения об учениках: «В классе учатся 40 школьников, в том числе 22 девочки. 25 школьников учатся на хорошо и отлично, в том числе 13 девочек. Туризмом занимаются 29 учеников, в том числе 12 девочек и 10 школьников учатся на хорошо и отлично. 9 девочек учатся на хорошо и отлично и занимаются туризмом». Докажите, что в этих сведениях есть ошибка.
Задание №3.
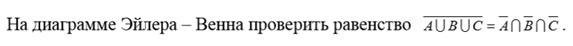
Задание №4.
 |
Составить по данной релейно-контактной схеме формулу (функцию проводимости).
Задание №5.

Запишите в виде формул алгебры логики высказывания:
Задание №6.
 |
Составьте таблицу истинности для следующих формул:
 |
Задание №7.
Задание №8.
 |
Постройте таблицы истинности для формул булевых функций трех переменных h (x, y, z) и g (x, y, z). Выясните, являются ли эти формулы равносильными.
Задание №9.
Запишите СДНФ и СКНК булевой функции трех переменных f (x, y, z), заданной вектором значений: f = (00100010).
Задание №10.
 |
Запишите словами следующие логические выражения и определите их истинность.
Задание №11.
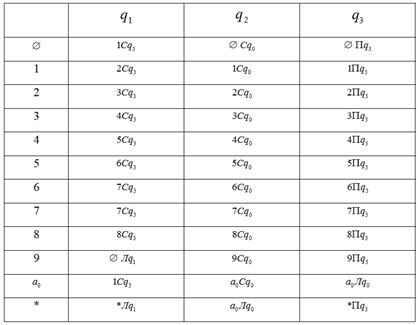 |
Найти результат работы машины Тьюринга
 над словом
над словом
Контрольная работа по математической логике
Вариант 9
Задание №1.
Даны множества В={2,3,4,5,6,7,8,9,10}; С={-4,-2,0,2,4,6,7,8,9,12}; А={-5,-3,-1, 0, 1, 3, 4, 5, 7, 9, 11, 13}. Задайте множества: а) (АÈВ)ÇС; б) АÇВÇС; в) (АÇС)\B; г)(A\B) Ç (C\B).
Задание №2.
Чтобы поступить в институт необходимо сдать три экзамена: географию, биологию и математику. Из 1500 абитуриентов экзамен по географии сдали 800 человек, по биологии – 700, по математике – 600. При этом 450 человек сдали экзамены по географии и биологии, 400 человек – по географии и математике, 300 человек – по биологии и математике, а 200 абитуриентов сдали все три экзамена. Сколько человек не сдало ни одного экзамена?
Задание №3.
 |
Задание №4.
 |
Составить по данной релейно-контактной схеме формулу (функцию проводимости).
Задание №5.

Запишите в виде формул алгебры логики высказывания:
Задание №6.
 |
Составьте таблицу истинности для следующих формул:
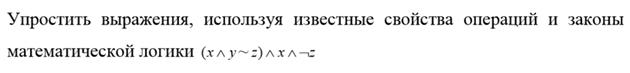 |
Задание №7.
Задание №8.
Постройте таблицы истинности для формул булевых функций трех переменных h (x, y, z) и g (x, y, z). Выясните, являются ли эти формулы равносильными.
 |
Задание №9.
Запишите СДНФ и СКНК булевой функции трех переменных f (x, y, z), заданной вектором значений: f = (01001010).
Задание №10.

Запишите словами следующие логические выражения и определите их истинность.
Задание №11.
 |
Найти результат работы машины Тьюринга
 над словом
над словом
Контрольная работа по математической логике
Вариант 10
Задание №1.
Даны множества А={-1,0,1,2,3,4,5,6,7,8}; В={-6,-4,-2,-1,0,2,6,7,9}; С={-7,-5,-3,-1, 0, 1, 3, 4, 5, 7}. Задайте множества: а) (АÈВ)ÇС; б) АÇВÇС; в) (АÇС)\B; г)(A\B) Ç (C\B).
Задание №2.
Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников учатся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом». Докажите, что в этих сведениях есть ошибка.
Задание №3.

Задание №4.
Составить по данной релейно-контактной схеме формулу (функцию проводимости).
 |
Задание №5.
 |
Запишите в виде формул алгебры логики высказывания:
Задание №6.
 |
Составьте таблицу истинности для следующих формул:
 |
Задание №7.
Задание №8.
 |
Постройте таблицы истинности для формул булевых функций трех переменных h (x, y, z) и g (x, y, z). Выясните, являются ли эти формулы равносильными.
Задание №9.
Запишите СДНФ и СКНК булевой функции трех переменных f (x, y, z), заданной вектором значений: f = (01010101).
Задание №10.
Запишите словами следующие логические выражения и определите их истинность.
 |
Задание №11.
 |
Найти результат работы машины Тьюринга
 над словом
над словом
