Приложение

Теоретический раздел ”Структурная надежность сетей связи”.
Надежностью какого-либо объекта (системы, сооружения, устройства или отдельной детали) называется его свойство, заключающееся в способности выполнять поставленные задачи в опреде­ленных условиях эксплуатации. Состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения ос­новных параметров в пределах, установленных нормативно-техни­ческой документацией, называют работоспособностью, а состояние, в котором объект удовлетворяет указанным требова­ниям, - его исправностью. Событие, заключающееся в нару­шении работоспособности объекта, называют отказом.
В зависимости от назначения объекта, выполняемых им функ­ций и условий эксплуатации различают несколько свойств объек­та, связанных с надежностью. К этим свойствам относятся:

• безотказность (свойство непрерыв­но сохранять работоспособность);
• долговечность (свойство сохранять рабо­тоспособность до определенного состояния);
• ремонтопригодность (возможность выполнения ремонта и технического обслуживания);
• восстанавливаемость (возможность восстановления работоспособ­ности после отказа);
• срок службы или сохраняемость.

Для сетей связи, являющихся сложными многофункциональны­ми системами, состоящими из элементов разнородных по своим свойствам, показателям надежности, назначению, дате изготовле­ния, сроку ввода в эксплуатацию и т. п., можно выделить два ос­новных аспекта надежности, которые условимся называтьаппара­турным и структурным.

Под аппаратурным аспектом будем пони­мать проблему надежности аппаратуры, отдельных устройств и их элементов, включая каналы и линейные тракты, т. е. отдель­ных элементов, входящих в узлы и линии сети.

Структур­ный аспект отражает функционирование сети в зависимо­сти от работоспособности или отказов узлов (станций, пунктов) или линий, магистралей, пучков каналов сети, т. е. он свя­зан с возможностью существования в сети путей доставки инфор­мации. В настоящем разделе будем говорить только о надежности, рассматривая сеть как единое целое. Надежность сети в этом случае будем называть структурной надежностью.
Учитывая многофункциональность сети, в которой при N уз­лах должно быть организовано N(N—1) связей, да еще разного вида (телеграф, телефон, звуковое или телевизионное вещание и т. п.), определить, что следует понимать под отказом сети, т. е. определить, когда сеть в целом перестает выполнять свои функции, практически невозможно. Иногда под отказом сети понимают потерю связности узлов. Однако этот показатель может быть при­нят только в некоторых частных случаях, так как он не учитывает важности отдельных связей. В других случаях надежность сети характеризуют некоторой «средней» величиной коэффициента го­товности (или другого показателя) связи или путей в сети для за­данных пар узлов. Более правильно, по-видимому, характеризо­вать надежность сети матрицей, вектором или перечнем показателей надежности линий или каналов сети или же для каждой пары пунктов сети — показателями надежности кратчайших или допустимых путей или всех воз­можных путей. Наконец, надежность сети может характеризоваться функциями (графиками) веро­ятностей того, что сохранится определенная часть из общего числа линий, путей или связей.
Будем относить понятие надежности не к сети в целом, а к пу­тям или совокупностям путей между заданной парой пунктов (уз­лов), т. е. рассмотрим надежность связи между этими пунктами, считая, что известны надежностные показатели линий и узлов. Тре­бования к надежности в таком понимании могут быть различными в зависимости от значения рассматриваемых пунктов, расстояний между ними, их взаимосвязанности в хозяйственной или другой деятельности, а также от вида и назначения связи. Заметим, что можно говорить: «сеть G1 надежнее сети G2», если при выполне­нии одинаковых функций в сети G1 надежность связей между все­ми заданными парами узлов не ниже, а между некоторыми — вы­ше, чем в G2.
Для связи между узлами (пунктами) a_S и a_T в сети исполь­зуются все возможные пути или выбранное по какому-либо при­знаку множество путей Mst. Каждый путь µ^К_ST (k-ый путь из множества путей от a_S к a_Т )состоит из линий и узлов, че­рез которые он проходит. Под показателем надежности пути (надежность пути) p^K _ST= p (µ^К st ) будем понимать вероятность того, что данный путь в про­извольный момент времени находится в работоспособном состоя­нии, а это означает, что работоспособными должны быть все линии и узлы, входящие в этот путь. Надежность связи будем оценивать вероятностью того, что работоспособным является хотя бы один путь.
Отказом линии будем называть такое состояние, при ко­тором каналы, образующие рассматриваемую линию, либо полностью вышли из строя, либо их параметры настолько ухуд­шились, что практически их нельзя использовать (например, из-за больших помех, искажений, снижения уровня на приемном кон­це и т. п.) для данного вида связи. Надежность лини - ве­роятность ее безотказной работы — определяется, с одной сторо­ны, аппаратурной надежностью ее элементов, а с другой, — меха­нической исправностью линейных сооружений. Основными причи­нами отказов линий являются различные механические повреждения, возникающие при проведении строительных работ (до 60—65%) или вследствие стихийных бедствий (молнии, разливы рек, оползни — до 10—15%). Реже они являются следствием де­фектов монтажа или строительства этих линий (8—15%) или неаккуратной работы обслуживающего персонала (2—10%). Число и длительность таких повреждений в значительной степени зави­сят от типа и устройства линий, их географического положения и уровня организации эксплуатационной службы. При равных усло­виях их число пропорционально длине линии.
Отказ узла — невозможность передачи через него информа­ции с входящих каналов на исходящие. Такой отказ эквивалентен одновременному отказу всех ребер, инцидентных этому узлу. Он происходит, как правило, в результате механических разрушений части или всего оборудования (в результате пожара, стихийного бедствия и т. п.). Отказ узла приводит к нарушению значительно большего числа путей, чем отказ линии, однако вероятность тако­го события значительно меньше вероятности отказа линии. рассматри­вать только влияние линий, считая, что Надежность каналообразующей и некоторой другой аппаратуры узла входит, как правило, в оценку надежности линий.
С точки зрения надежности линии сети принадлежат к элементам с восстановлениями. Процесс функционирования восста­навливаемого элемента можно представить как последовательность интервалов работоспособности и простоя (восстановления) (рис.11.1). Длительности этих интервалов определяются всеми фак­торами, о которых говорилось выше.

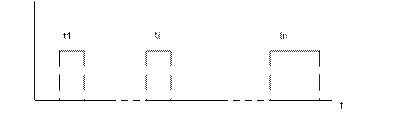
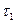
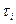
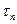
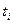- интервал работоспособности; 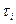- интервал простоя.

Рис. 8.1. Интервалы работоспособности и простоя (восстановления).

В первом приближении интервалыможно считать взаимно независимыми случайными величинами, имеющими определенное распределение со средними временами. Тогда среднее время безотказной работы 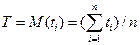(иногда эту величину называют наработкой на отказ) и среднее время восстановления

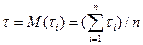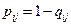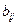. Под надежностью линии будем понимать вероятность нахождения линии в состоянии работоспособности или математи-ческое ожидание доли времени, в течение которого линия находится в исправном состоя­нии (это определение эквивалентно понятию коэффициента готов­ности):
,
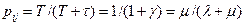где λ= 1/Т - интенсивность отказов;
µ =1/ 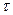- интенсивность вос­становления;
.
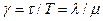При малых значениях величины y можно принять:

.
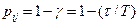Аналогичным образом определяется вероятность отказа ребра bij: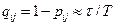
Под живучестью сети чаще всего понимают ее свойство со­хранять связность при массовых разрушениях узлов и линий связи сети и обеспечивать при этом связь между всеми или большинством пунктов хотя бы с по­ниженным качеством. В настоящее время нет установленного кри­терия для оценки живучести. Под живучестью сети будем по­нимать сохранение ее связности.

Показатели структурной надежности сети и методы их определения

Важным качественным показателем элементов сети являетсякоэффи­циент готовности Kг - вероятность исправного (работоспособного) состояния данного элемента в произвольный момент времени в процессе эксплу-атации. Иногда под отказом сети понимают потерю связности, однако этот по­казатель не учитывает важности связей. В других случаях надежность сети характеризуется некоторой "средней" величиной коэффициента готовности связи и путей в сети для заданных пар узлов. Более правильно характеризо­вать надежность сети матрицей, вектором или перечнем показателей надёжности линий сети или же для каждой пары пунктов сети использовать показатели надеж­ности кратчайших или допустимых путей ("реальная" надежность связи) или всех возможных путей ("потенциальная" надежность).
При исследовании структурной надежности можно рассматривать две модели сети: детерминированная сеть или сеть стохастическая (вероятностная) в зависимости от того, учитывается или игнорируется случайный характер внешних или внутренних воздействий на элементы модулируе­мой реальной сети связи. Элементыдетерминировнной сетипринимают абсолютно надёжными элементами или абсолютно ненадежными. Встохастическойсетинекоторые или все элементы обладают конечной надежностью (0 < pi < 1).
Одним из важнейших вопросов при решении задач анализа и син­теза сетей связи с учетом структурной надежности является выбор показателей или системы показателей структурной надежности. Испо­льзуемые в настоящее время показатели можно условно разбить на две группы:

· структурные показатели;

· вероятностные показатели.

К структурнымпоказателямотносятся такие показатели, как избыточность, коэффициент влияния элемента сети на структурные свойства сети и др.
Квероятностным - надежность путей и связи, вероятность связности нескольких или всех узлов сети, математическое ожидание числа связи в сети и т.д.

При использовании первой группы показателей сеть связи рассматри­вается как детерминированная. При этом избыточность характеризует избыток линий и узлов по сравнению с минимально необходимым чис­лом для обеспечения связи между различными оконечными пунктами. Количественно избыточность может быть оценена числом независимых по ребрам или вершинам путей, которые могут быть использованы для организации связи между фиксированной парой узлов. Коэффициент влияния оценивает влияние утраты или выход из строя узла или линии связи на возможности сети с точки зрения обеспечения связи между пунктами сети.

При использованиивторой группы показателей структурной на­дежности сеть представляется в виде взвешенного графа. В качестве весов элементов графа сети (вершин или ребер) в этом случае используются, например, коэффициенты готовности. Как правило, предполагается, что элементы графа являются статистически независимыми. Для оценки структурной надежности стохастической сети могут быть ис­пользованы следующие показатели:

· надежность пути или надежность связи (вероятность связности двух узлов сети);

· вероятность связности нескольких (n > 2) или всех узлов сети;

· математическое ожидание числа связей в сети и др.

Под надежностью пути, связывающего узел i с узлом j, будем понимать вероятность исправного состояния всех линий и узлов, образующих этот путь. Надежность связи или вероятность связ­ности двух узлов - это вероятность существования хотя бы одного пути в работоспособном состоянии из заданного множества путей.

Вероятность связности нескольких или всех узлов сети представ­ляет собой вероятность того, что одновременно между несколькими или всеми узлами сети существует связь.

Математическое ожидание числа связей в сети определяет сред­нее число связей в сети при фиксированной надежности элементов сети (узлов и линий связи).

Аналитические методы определения показателей структурной надежности

Рассмотрим задачу определения вероятности связности меж­ду узлами а_S и а_t, если задано множество путей M_St , которые могут быть использованы для этой связи, и извест­ны надежность 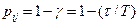всех ребер 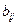сети, образующих пути. Надежность 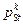пути 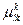, при условии статистической независимости элементов сети, оценим вероятностью одновременного работоспособного состояния всех ребер, образующих этот путь, т. е.

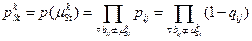(8.1)

где 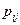– показатель надежности линии ij, принадлежащей пути между узлами s и t.
Если учитывать надежность узлов, то

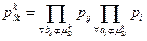(8.2)

где 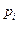– показатель надежности i – ого узла, входящего путь между узлами s и t.
Вероятность связности 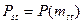двух узлов а_s и a_t будем оценивать вероятностью исправного состояния хотя бы одного пути из заданного множества 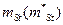. Когда отдельные элементы пути (их участки или линии связи) составляют параллельно-последовательную структуру, то для определения вероятности связности можно использовать обычные методы определения надежности структур с таким соединением элементов. При последовательном соединении можно пользоваться формулой (11.1), а при параллельном соединении элементов общая надежность рассчитывается по формуле

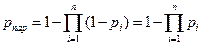, (8.3)

где pi- надежность каждого элемента;

n- число параллельно-соединенных элементов.

На рисунке 8.2 приведен пример параллельно-последовательной структуры

и с мостиковым соединением по отношению к узлам 1и 3.

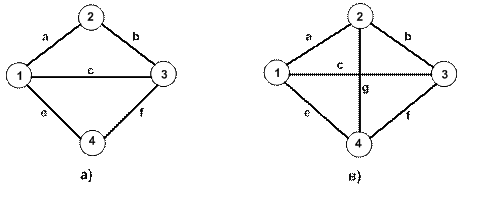
Рис. 8.2 Пример структур сети параллельно-последовательной (а) и с мостиковым соединением (б) по отношению к узлам 1 и 3

Если в структуре сети имеются мостиковые соединения, то ис­пользовать приведенные выше формулы для определения вероятности связности узла 1 с узлом 2 нельзя. Напри­мер, для структуры рис. 8.2б, отличающейся от структуры рис.8.2а наличием ребра g.

Одним из методов расчета вероятности связности (надежности свя­зи) Pst между узлами as и at для сложной (мостиковой) структуры является метод последова-тельного разложения структуры. Метод основан на том свойстве, что надежность

структуры , включающей ребро 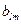с надежностью 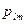, рав­нa:

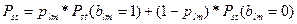, (8.4)
где 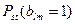- надежность связи в сети, в которой p_lm=1, т. е. узлы а_l и а_m слиты;
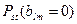- надежность связи в сети при p_lm = 0 , т. е. из сети изъято ребро b_lm.
Разложение (вынос ребер) производится до тех пор, пока ос­тавшиеся структуры не будут параллельно-последовательными. Метод последовательного разложения позволяет определить потенциальную надежность связи между заданными узлами в виде функции или числового значения. Однако он не работает в случае, если необходимо определить надежность заданного мно­жества путей m_st, меньшего, чем множество всех путей между узлом s и t.
Для определения вероятности связности узла s с узлом t в этом случае можно воспользоваться следующей методикой:

1. Определим список путей, которые могут быть использованы для связи узла s с узлом t.

2. Каждому пути поставим случайное событие Ak, характеризующее исправное состояние данного пути.

3. Определим надежность каждого из указанных путей c учетом заданных

показателей надежности элементов сети. Полученная функция определяет

вероятность наступления события Ak.

4. Воспользуемся формулой для расчета вероятности суммы совместных событий Ai,поставленных в соответствие множеству путей между узлами

s и t.

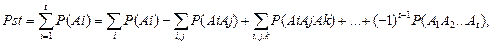(8.5)

где t - число путей, которые могут быть использованы для связи узла i с узлом j;

Ai– событие, поставленное в соответствие i-ому исправному пути из множества путей k = (1,t);

P (А_i) – вероятность наступления события А_i;

P (А_i А_j) – вероятность совместного наступления двух событий А_к и А_m;

P (А₁ А₂ …А_t) – вероятность совместного наступления t событий Аi;

P (UA_i) – вероятность наступления хотя бы одного события А_i из множества k = (1,t).

С учетом условия совместного наступления событий Аi, показатели коэффициентов готовности элементов сети, входящих в любое из указанных выше выражений в формуле для расчета вероятности суммы совместных событий, заменяются на первую степень.
Для определения математического ожидания числа связей в сети М (Х) воспользуемся следующим алгоритмом:

· Определим число интересующих нас пар взаимодействующих узлов сети.

· Определим списки путей, которые могут быть использованы для доставки информации для каждой пары узлов сети из заданного списка.

· Для каждой пары узлов определим вероятность их связности по выше изложенной методике.

· Произведем суммирование значений вероятностей связности различных пар узлов сети.

В результате получим абсолютное значение математического ожидания числа связей сети – М (Х). Удобнее и нагляднее данную величину выразить в относительных единицах. Тогда величина М (Х)_отн. может быть рассчитана по формуле:

М (Х)_отн. = (М (Х)/N_max)·100% , (8.6)

где N_max – максимальное (заданное) число связей в сети при условии, что все элементы сети абсолютно надежны.

Метод статистических испытаний

Наиболее универсальным методом, который пригоден для решения задач практически любой сложности, являетсяметод статистических испытаний (метод Монте-Карло).Метод заключается в построении математической модели системы, реализация которой осуществляется в виде программы для ЭВМ. Основная идея этого методаосновывается на наличии связи между вероятностными ха­рактеристиками различных случайных процессов и величинами, явля­ющимися решениями задач математического анализа. Вместо вычисления ряда сложных аналитических выражений можно эк­спериментально определить значения соответствующих вероятностей или математических ожиданий. Этот метод получил широкое развитие в связи с новыми возможностями, которые дают современные ЭВМ. В основе метода лежит техника генерации конечных наборов значений случайной величины в соответствии с ее функцией распре­деления вероятностей.Будем предполагать, что в рамках метода статических испытаний существует возможность воспроизвести слу­чайную последовательность значений случайной величины или слу­чайную последовательность значений объекта, если задана функция распределения этой величины или распределение вероятностей сос­тояний объекта. Метод статических испытаний обычно используется для опреде­ления с ограниченной точностью того или иного стохастического параметра объекта “a “ путем вычисления его несмешанной выборочной оценки a^*_N на основании имитации механиз­ма возникновения случайной величины или случайного события. Точность вычисляемой оценки растет с увеличением объема выборки N. Увеличение точности, например, в десять раз приводит к сто­кратному удлинению времени решения задачи (числа испытаний). По­этому метод статических испытаний не может быть использован для получения решений с очень большой точностью. В практических задачах этот метод дает точность порядка 0,01- 0,001 от максимального значения. Метод статических испытаний хорошо приспособлен к многомер­ным задачам. Обычно эти задачи и не требуют большой точности, поэтому отмеченный недостаток метода не столь существенен. Особенности этого метода сводятся к следующему:

· сравнительная простота и однородность последовательности