Расчет элементов линии заданного пути

Маршрут полета в ПНПК задается геодезическими координата­ми ИПМ, ППМ и КПМ. Геодезические координаты в бортовой цифровой вычислительной машине пересчитываются в сферические. По сферическим координатам начальной и конечной точек этапа маршрута рассчитываются следующие элементы линии заданного пути:

• заданные путевые углы по этапам маршрута;
• длина этапа;
• угол схождения меридианов;
• линейное упреждение разворота.

Расчет заданных путевых углов по этапам маршрута.

В ПНПК заданные путевые углы по этапам маршрута измеряются от условного меридиана, в качестве которого принимается истинный меридиан, проходящий через ИПМ.

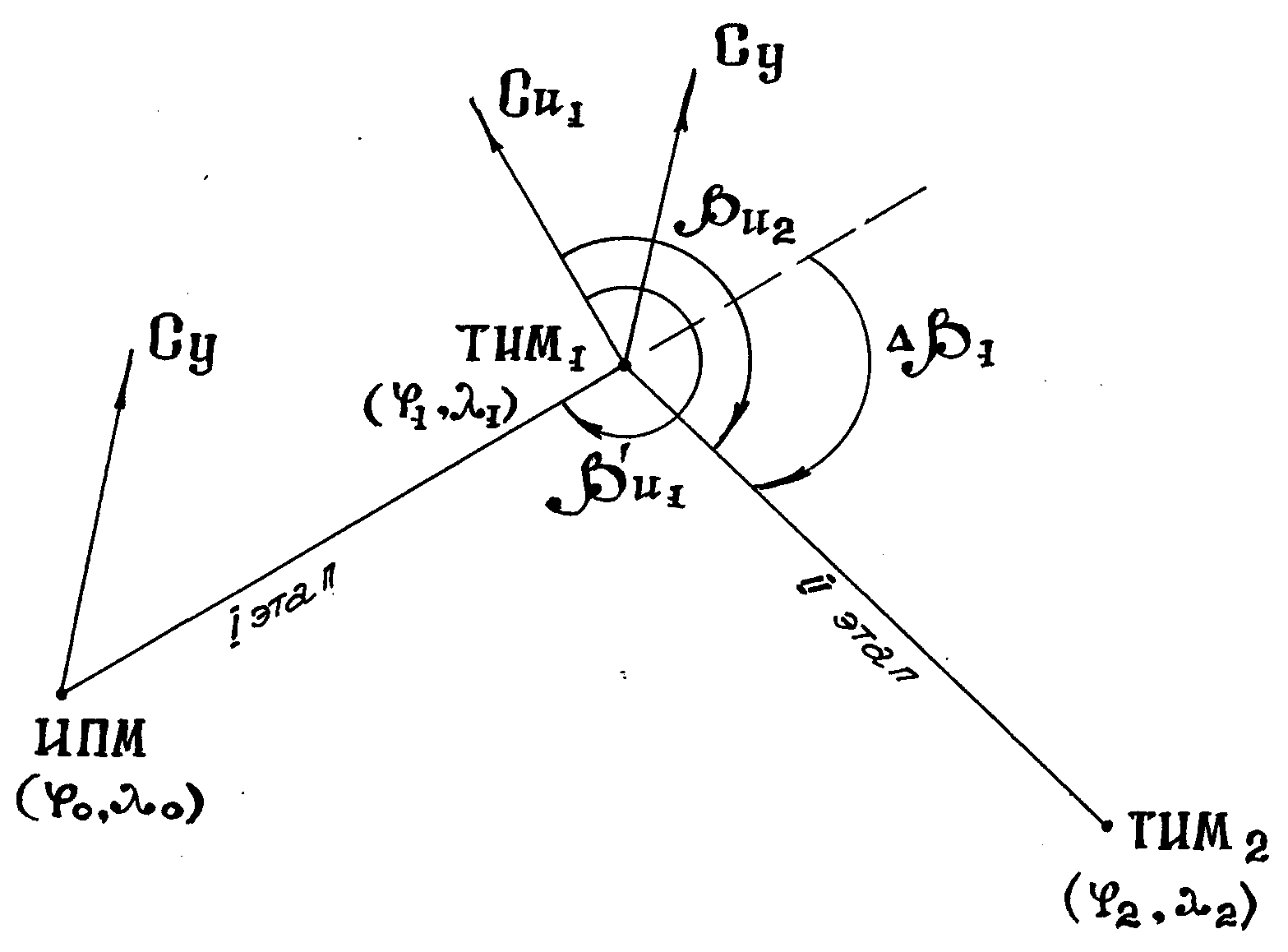
Для первого этапа маршрута заданный условный путевой угол b_y1 (он же начальный заданный истинный путевой угол β_и1) рассчитывается из сферического треугольника ИПМ-Рс-ТИМ₁ по формуле четырех элементов:

cos(90˚– φ₀) cos(λ₁ – λ₀)=sin(90˚– φ₀) ctg(90˚– φ₁) – sin(λ₁–λ₀) ctg β_и1.

Упростив полученное выражение по формулам приведения, имеем:

sin φ₀ cos(λ₁ – λ₀) = cos φ₀ tg φ₁ – sin(λ₁–λ₀) ctg β_и1.

Решив данное уравнение относительно ctg β_и1, получим:

ctg β_и1 = .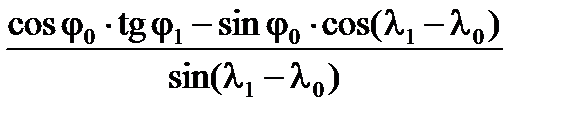

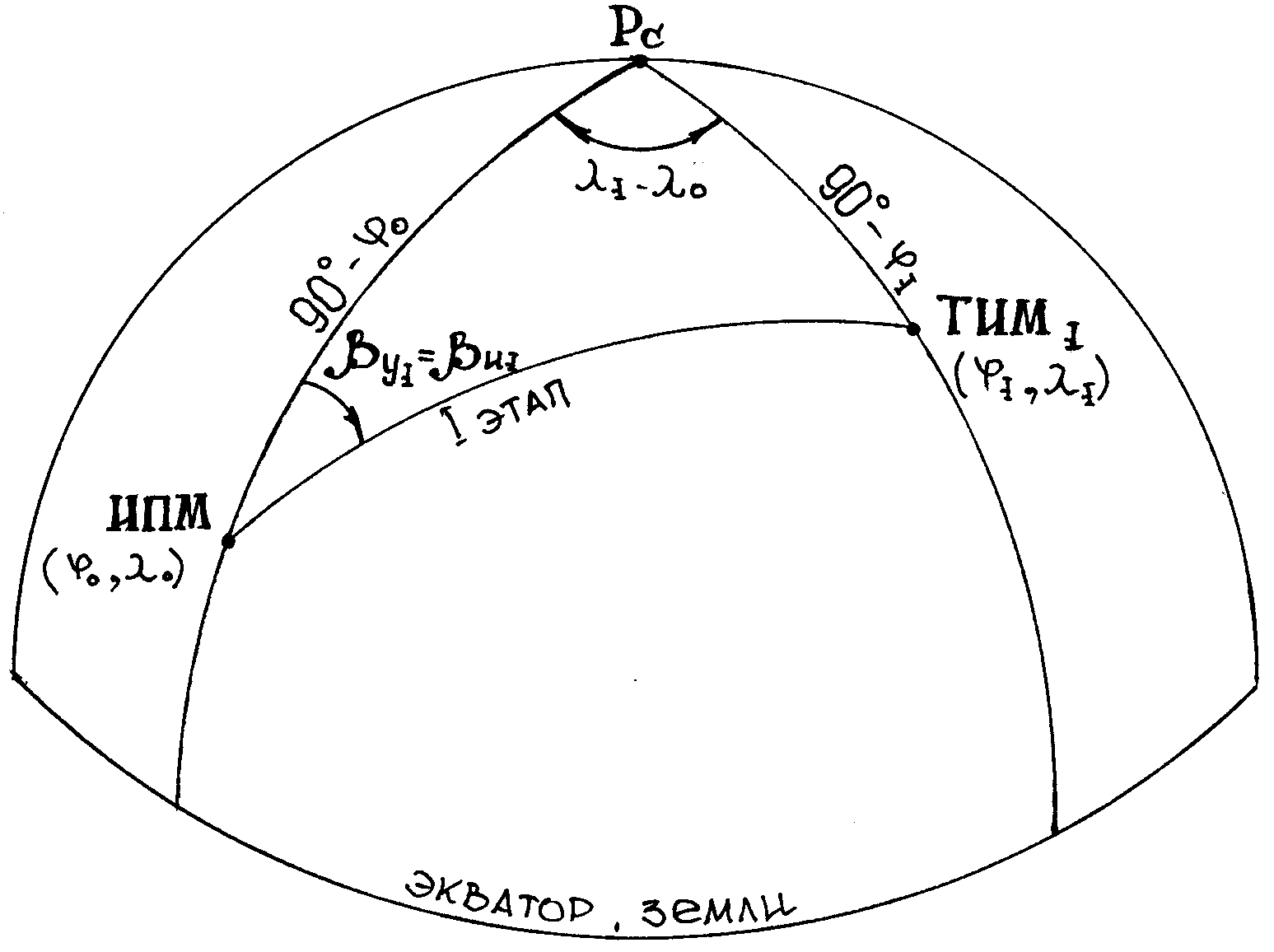Рис. Расчет путевого угла первого этапа маршрута

Для удобства решения в БЦВМ от функции котангенса в выражении перейдем к тангенсу путевого угла, учитывая, что тангенс – функция обратная котангенсу. Тогда значение β_и1 можно представить в виде:

tg β_и1 = .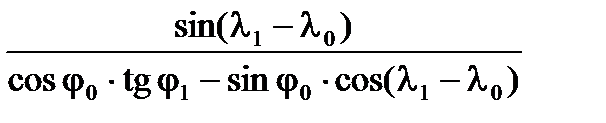

По формуле в БЦВМ рассчитывается заданный условный путевой угол первого этапа маршрута.

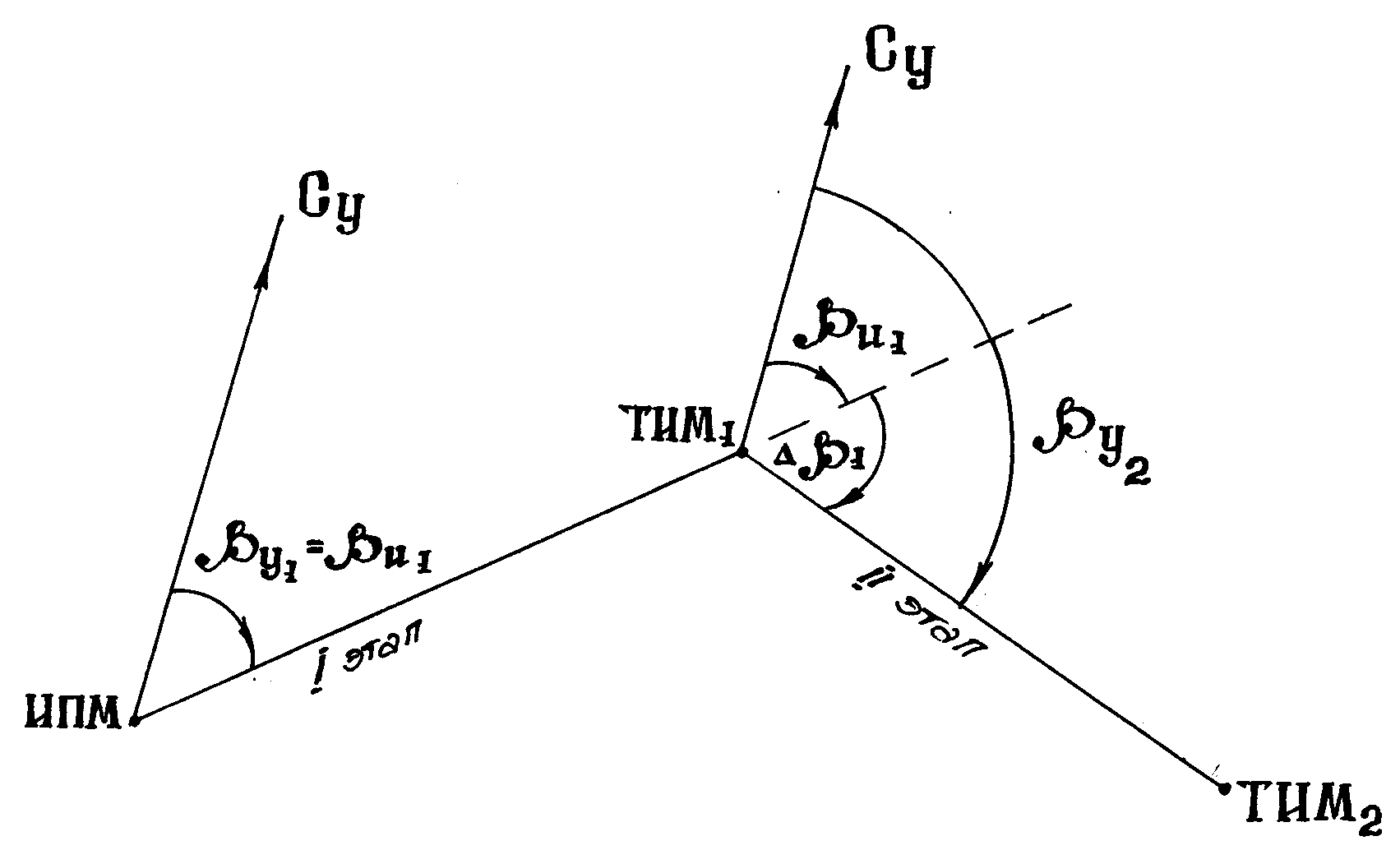
Рис. Определение заданного путевого угла второго этапа маршрута

Заданный условный путевой угол второго этапа маршрута b_y2 рассчитывается как:

b_y2 = bи₁ + Db₁,

где Db₁ – угол разворота для выхода на линию заданного пути второго этапа маршрута.

Угол разворота для выхода на ЛЗП второго этапа маршрута рассчитывается по формуле, получаемой из рисунка:

Db₁ = β_и2 – (β'_и1 – 180°) = β_и2 + 180° – β'_и1,

где β_и2 – начальный заданный истинный путевой угол второго этапа маршрута;

β'_и1 – обратный истинный путевой угол предыдущего (первого) этапа маршрута в первой ТИМ.

Для расчета начального заданного истинного путевого угла второго этапа маршрута в уравнении вместо координат ИПМ подставим координаты ТИМ₁, а вместо координат ТИМ₁ – координаты ТИМ₂.

В результате этого получим:

tg β_и2 = .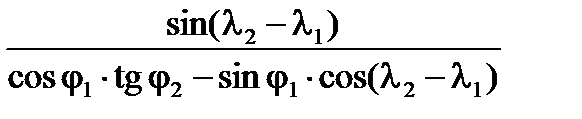

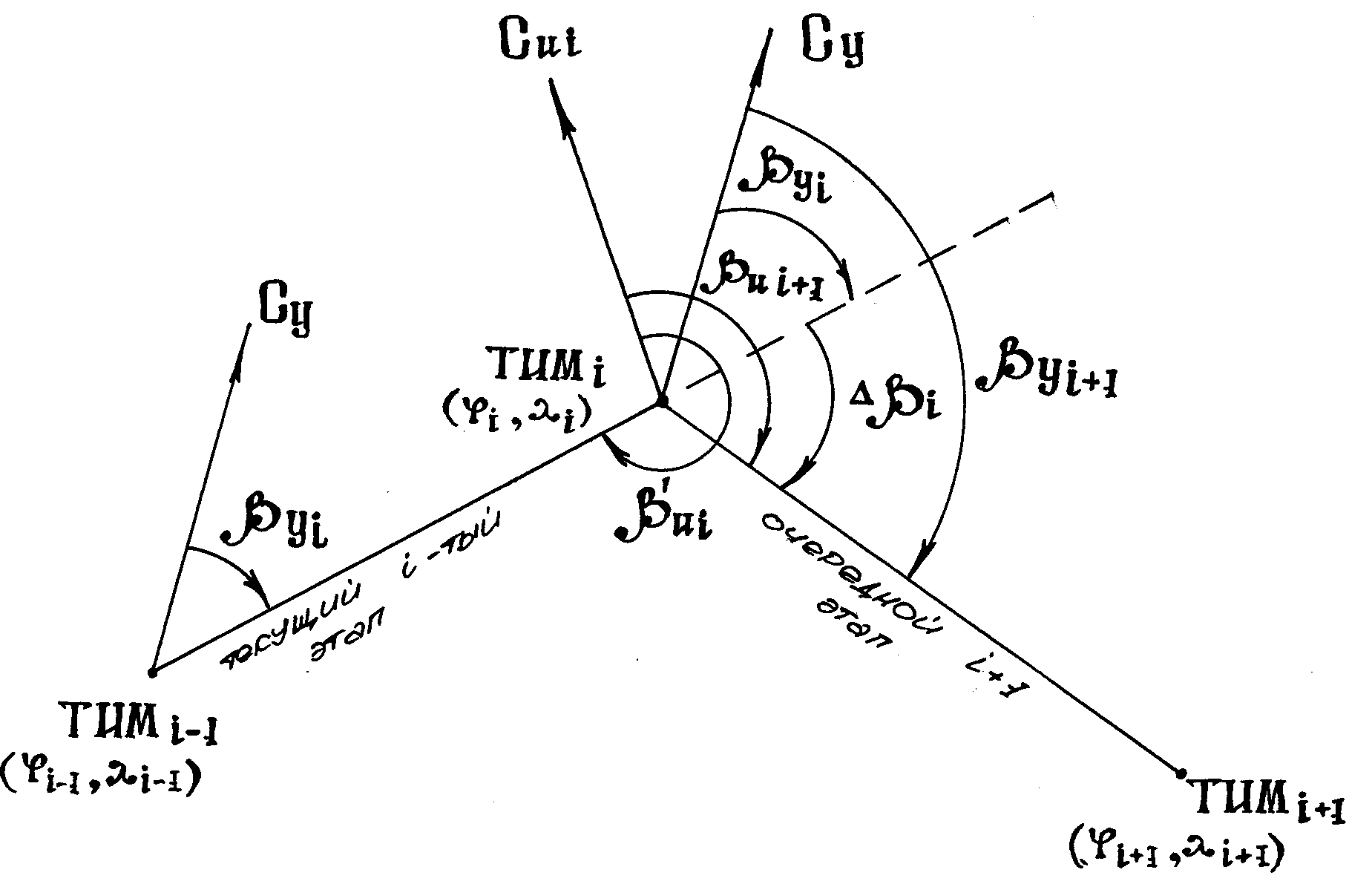Рис. Расчет угла разворота Db₁

Для любого очередного (i + 1) этапа маршрута заданный условный путевой угол b_yi+1 рассчитывается как сумма заданного путевого угла b_yi текущего i-того этапа маршрута и угла разворота Db_i для выхода на линию заданного пути очередного (i + 1) этапа, т. е.

b_yi+1 = b_yi + Db_i, где

Db_i = β_иi+1 + 180° – β'_иi,

tg β_иi+1 =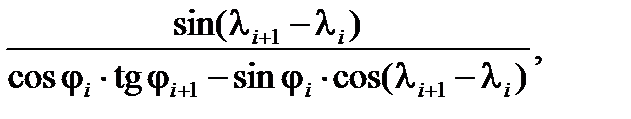

tg β'_иi =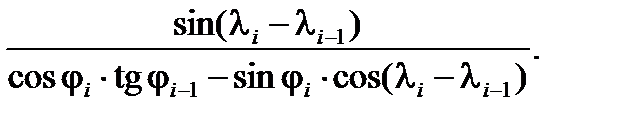

Заданный условный путевой угол этапа маршрута ндицируется на указателе штурмана

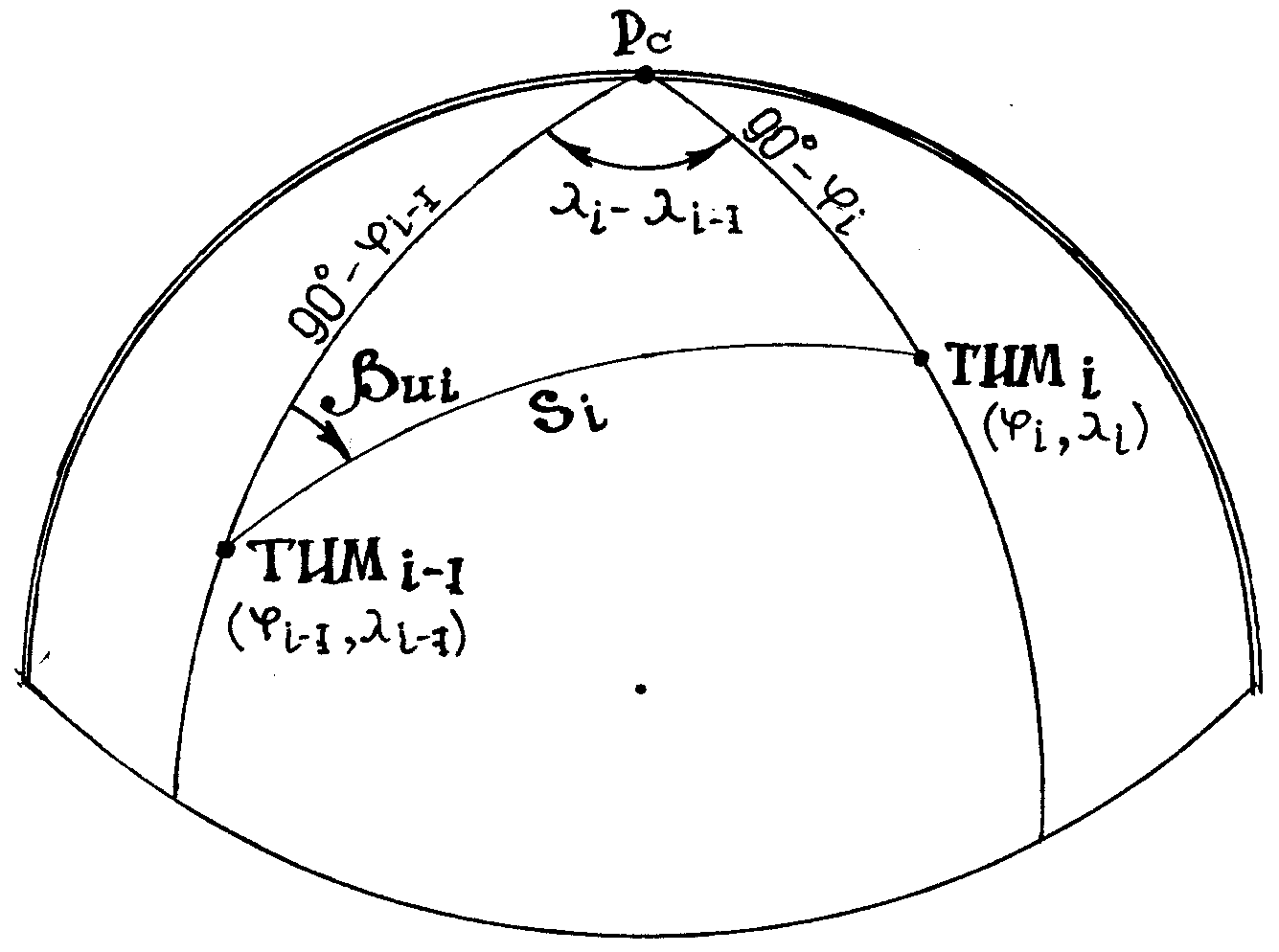Рис. Расчет заданного путевого угла для любого УШ-3 точной курсовой системы ТКС-П с очередного (i + 1) этапа маршрута помощью индекса заданных путевых углов

(ЗПУ) при установке переключателя ИНДЕКС УШ

на приборной доске штурмана в положение ЗПУ и на навигационных пилотажных приборах НПП летчиков и штурмана с помощью стрелки ЗК при установке переключателя режимов работы на пульте управления САУ в положение НАВИГАЦИЯ. Кроме того, заданный условный путевой угол этапа маршрута индицируется на верхней строчке индикатора КП1-10м при наборе адреса 354 и нажатии клавиши ИНДИКАЦИЯ на панели управления.

Расчет длины этапа маршрута

Длина этапа маршрута в радианах рассчитывается из сферического треугольника ТИМ_i-1–Рс-ТИМ_i по теореме синусов:

.

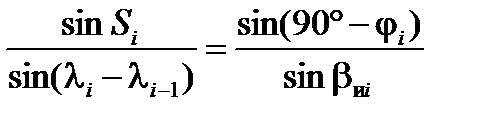Решая это уравнение относительно длины этапа маршрута S_i, имеем:

.

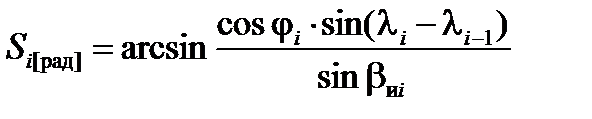Рис. Расчет длины i-того этапа маршрута

Длина этапа маршрута в километрах рассчитывается по формуле:

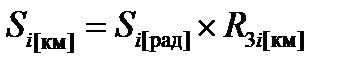, где R_3i – радиус земной сферы в километрах.

Расчет угла схождения меридианов

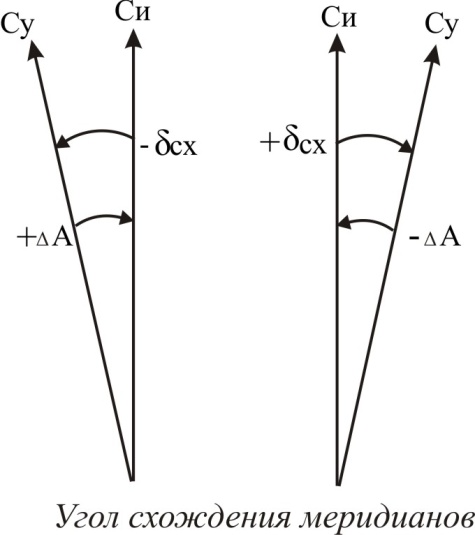Под углом схождения меридианов d_сх понимается угол, заключенный между истинным меридианом данной точки и условным меридианом, выбранным за начало отсчета. Угол схождения меридианов отсчитывается от 0º до +180º по ходу часовой стрелки («+») и от 0º до –180º против хода часовой стрелки (« ̶ »).

Из определения угла схождения меридианов следует, что он по абсолютной величине равен азимутальной поправке DА (в случае, когда за условный меридиан принимается истинный меридиан какой-то точки, выбранный за начало отсчета) и противоположен ей по знаку.

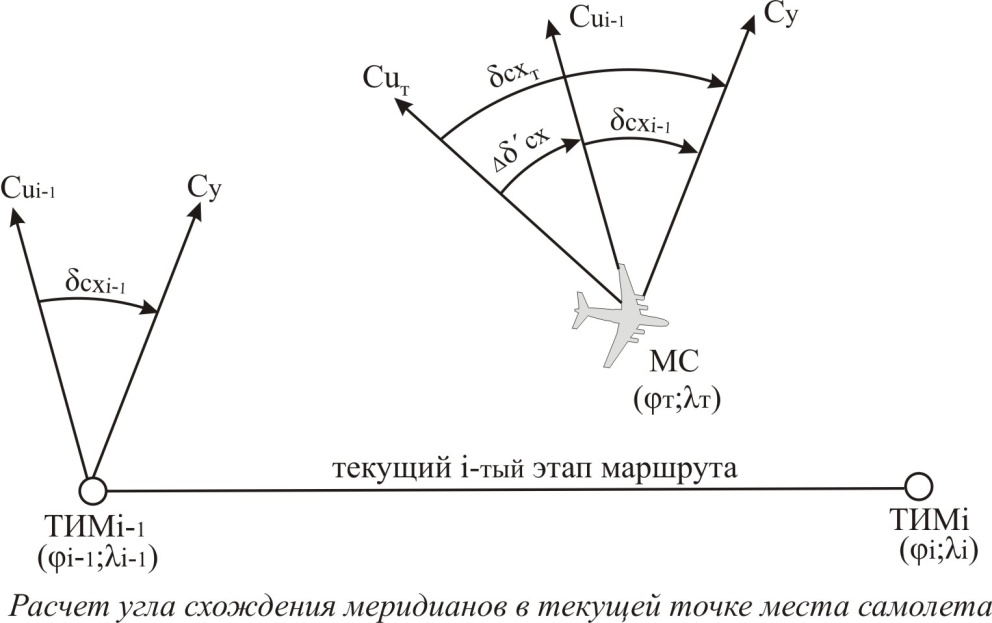
В ПНПК угол схождения меридианов определяется с повышенной точностью в точке излома маршрута как разность истинных путевых углов, рассчитанных в начале и конце одного и того же этапа маршрута и приближенно в текущей точке места самолета.

Расчет угла схождения меридианов в точке излома маршрута

Так как в качестве условного меридиана в ПНПК принимается истинный меридиан ИПМ, то в точке ИПМ угол схождения меридианов равен d_сх0 = 0.

В первой точке излома маршрута угол схождения меридианов равен:

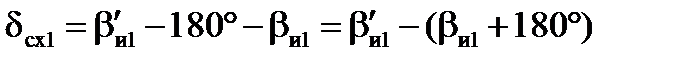
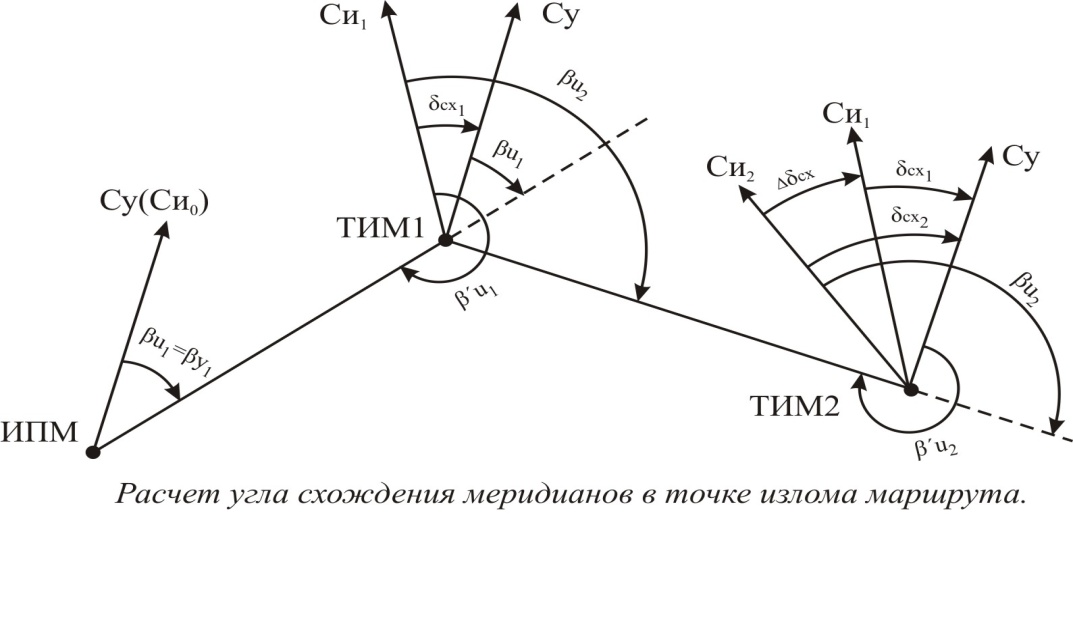
Во второй ТИМ угол схождения меридианов равен:

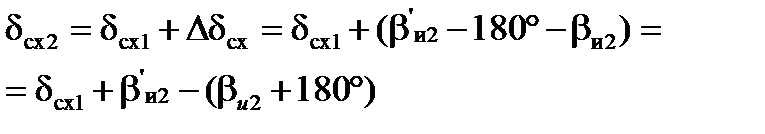
Таким образом, в любой i-той ТИМ угол схождения меридианов будет равен:

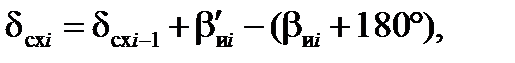
где i – номер очередной ТИМ, в которую выводится самолет;

d_схi-1 – угол схождения меридианов в предыдущей ТИМ_i-1;

β'_иi – обратный ИПУ текущего i-того этапа маршрута, измеренный в конце этапа;

β_иi – начальный истинный путевой угол этапа маршрута.

Угол схождения меридианов в предыдущей ТИМ_i-1 индицируется на верхней строчке индикатора КП1-10м при наборе адреса 527, а угол схождения меридианов в очередной ТИМ_i – при наборе адреса 530 и нажатой клавише ИНДИКАЦИЯ на КП1-10м.

Расчет угла схождения меридианов в текущей точке места самолета

В текущей точке места самолета угол схождения меридианов d_схт рассчитывается по приближенной формуле:

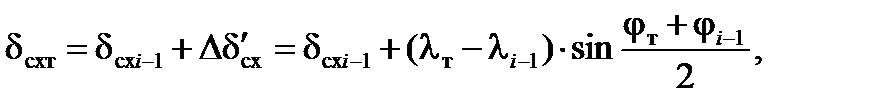
где l_т, j_т – текущие сферические координаты места самолета;

l_i-1, j_i-1 – сферические координаты предыдущей ТИМ_i-1;

d_cxi-1 – угол схождения меридианов в предыдущей ТИМ _i-1.

Угол схождения меридианов в текущей точке места самолета d_схт индицируется на верхней строчке индикатора КП1-10м при наборе адреса 531, и нажатой клавише ИНДИКАЦИЯ.

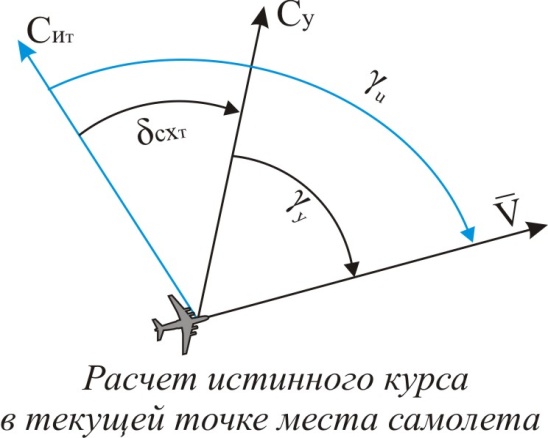
На последующих модификациях управляющего вычислительного комплекса (УВК) (где имеется клавиша 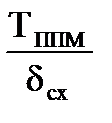) угол схождения меридианов в текущей точке места самолета индицируется на нижней строчке индикатора КП1-10м при включении данной клавиши. По адресу 531 в этом случае индицируется истинный курс g_и, рассчитанный по формуле:

,

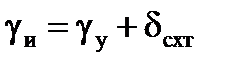где g_у – условный курс самолета, измеренный ТКС-П и выдаваемый в УВК.

Это дает возможность выполнить коррекцию показаний точной курсовой системы ТКС-П по данным инерциальной навигационной системы И-11-76.

Расчет линейного упреждения разворота.

При выходе на очередной этап маршрута разворот самолета начинается над точкой, удаленной от центра ППМ на величину линейного упреждения разворота (ЛУР).

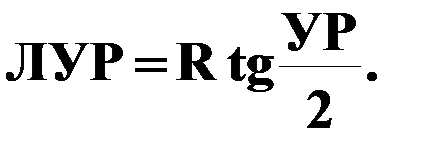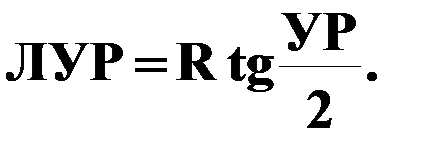Из прямоугольного треугольника:

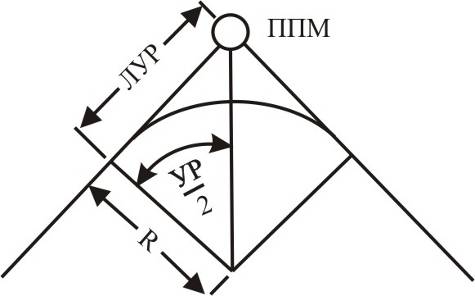Расчет линейного упреждения разворота в ПНПК производится по более сложной формуле с учетом влияния ветра и времени вво­да самолета в максимальный крен и вывода из него.

Величина ЛУР рассчитывается в ПНПК за 40км до ППМ. При угле разворота ³ 174° величина ЛУР принята постоянной и рав­на 40км. УВК не рассчитывает ЛУР, если:

- угол разворота меньше 11˚15′;

- ППМ маркирован признаком ЦЕЛЬ или КПМ;

- полет выполняется на 5-м участке предпосадочного маневра;

- не введены координаты следующего ППМ.

Счисление пути в ПНПК «Купол-76»

Под счислением пути понимается непрерывное определение текущих координат места самолета. В ПНПК используется комбинированный воздушно-доплеровский способ счисления пути, при котором датчиками параметров движения самолета являются доплеровский измеритель скорости и сноса (ДИСС), система воздушных сигналов (СВС) и точная курсовая система (ТКС-П).

Счисление пути в ПНПК осуществляется в этапно-ортодромической системе координат на основании данных о составляющих вектора путевой скорости Wx,Wz. Счисление пути включается нажатием на клавишу РАБОТА на панели управления КП1-10м, при этом одновременно производится расчет элементов линии заданного пути первого этапа маршрута, а на приборных досках летчиков и штурмана загорается табло МАРШРУТ.

При выводе уравнений счисления пути будем считать, что полет выполняется вблизи ЛЗП этапа маршрута, т. е. координата z места самолета близка к нулю.

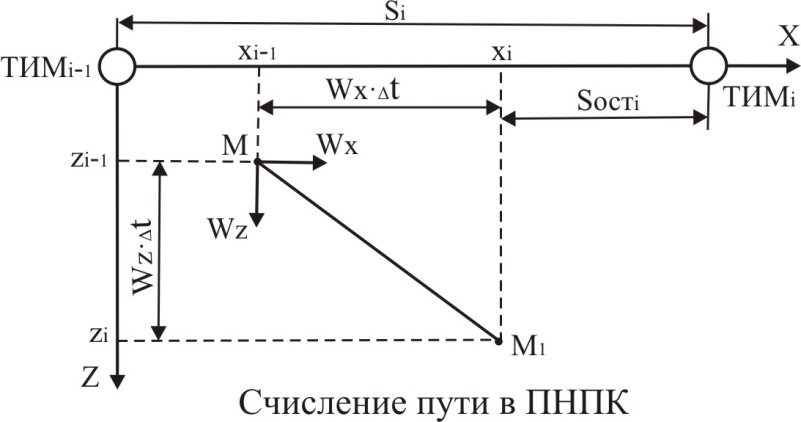Пусть в некоторый момент времени самолет находится в точке М с этапно-ортодромически-ми координатами x_i-1 и z_i-1.

Составляющие путевой скорости по осям этапно-ортодромической системы координат равны w_x и w_z. Тогда через малый промежуток времени Dt самолет сместится в точку М₁, координаты места самолета получат приращения по оси Х w_x^. Dt, а по оси Z w_z Dt и станут:

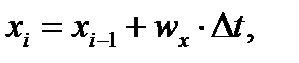
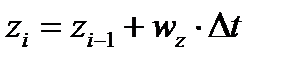
Эти уравнения являются уравнениями счисления пути для одного цикла работы БЦВМ. Промежуток времени Dt между двумя последовательными решениями задачи определения текущих координат места самолета называются длительностью цикла и в ПНПК составляет 0,5 с. Т.е. задача счисления пути в БЦВМ решается дискретно. Для n циклов работы БЦВМ уравнения счисления пути можно записать в виде:

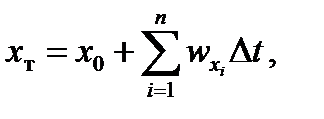
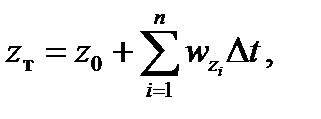
где x_т, z_т – текущие (счисленные) координаты места самолета;

x₀, z₀ – координаты точки счисления пути;

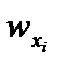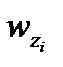, – составляющие путевой скорости по осям этапно-ортодромической системы координат при i-том цикле работы БЦВМ.

По рассчитанной длине этапа маршрута Si и текущей координате места самолета x_т рассчитывается оставшееся расстояние Sост_i до очередной ТИМ_i .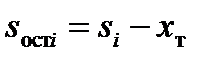

Оставшееся расстояние до очередной ТИМ_i и текущая координата места самолета z_т индицируются с точностью до десятых долей километра на цифровых счетчиках панели индикации при включенных клавишах в ряду ИНДИКАЦИЯ на панели управления КП1-10м. Кроме того, координату х_т можно прочитать на цифровых счетчиках панели индикации по адресу 401, а координату z_т – по адресу 403 при нажатой клавише ИНДИКАЦИЯ на панели ввода КП1-10м. Точность определения места самолета счислением пути в ПНПК характеризуется средней квадратической радиальной ошибкой: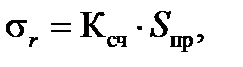

где К_сч – коэффициент счисления, равный 0,02 при определении составляющих путевой скорости с помощью ДИСС и 0,025 при определении составляющих путевой скорости по данным СВС-ПН-15 и коррекции ветра через каждые 20 минут полета;

S_пр – расстояние, пройденное самолетом без коррекции результатов счисления пути.

Физический смысл средней квадратической радиальной ошибки в определении координат места самолёта заключается в следующем:

- расчетное место самолёта может отстоять от фактического с гарантийной вероятностью Р_г = 0,632 на величину не более s_r или, иными словами, отметка места самолета не выйдет за пределы круга радиуса, равного s_r с гарантийной вероятностью Р_г = 0,632;

- отметка места самолёта не выйдет за пределы круга радиуса, равного 1,73s_r с гарантийной вероятностью Р_г = 0,95.

По индицируемым на цифровых счетчиках панели индикации КП1-10м координатам S_{ост i} и Z_т штурман графически прокладывает место самолёта на карте, для чего от очередной ТИМ_i по ЛЗП в сторону предыдущей ТИМ_i-1 отложить S_{ост i} в масштабе карты. Из полученной точки восстановить перпендикуляр к ЛЗП и, отложив на нем в масштабе карты координату Z_т со своим знаком, получить расчетную точку места самолёта.

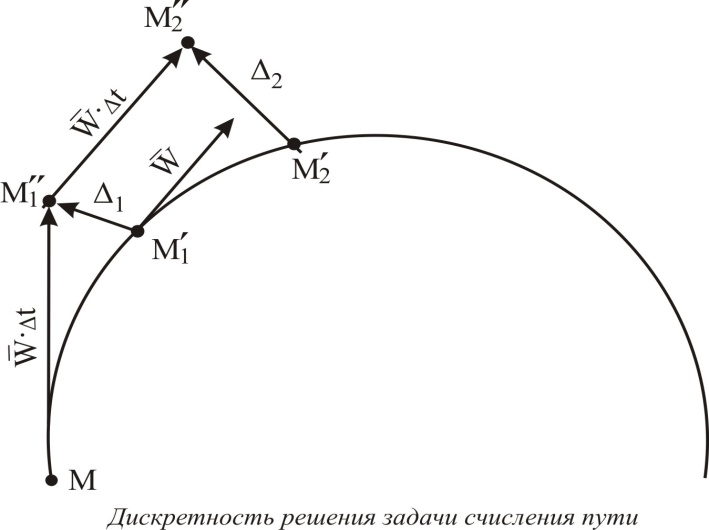
Дискретность решения задачи счисления пути через промежутки времени Dt = 0,5 с является причиной того, что при полете самолета с разворотом возникает ошибка в определении координат места самолёта. Пусть в точке М самолет вошел в разворот, и фактические координаты места самолёта совпали с расчетными. Двигаясь по криволинейной траектории, самолет через промежуток времени Dt = 0,5 с будет находиться в точке М₁'. БЦВМ не учитывает поворот вектора путевой скорости в процессе разворота и выдает расчетные координаты места самолёта в точке М₁". Из точки М₁' самолет, продолжая разворот, через очередной промежуток времени Dt = 0,5 с сместится в точку М₂', а БЦВМ выдает расчетное место в точке М₂".

Величина ошибки счисления пути D зависит от путевой скорости самолета, радиуса кривизны траектории (угла крена в развороте) и от суммарного угла разворота. Так, например, при путевой скорости w = 500 км/ч, угле крена в развороте b_кр = 30° и угле разворота Db = 360° величина ошибки D составляет 400 м.