Классификация ошибок измерении. свойства случайных ошибок

Ошибки измерений подразделяют на грубые, систематические и случайные. К грубым ошибкам относят ошибки, вызванные промахами и просчётами наблюдателя, неисправностями приборов, резким ухудшением внешних условий и др. С целью их обнаружения измерения выполняются многократно (не менее двух раз). Результаты измерений, содержащие грубые ошибки, необходимо выявлять и исключать из обработки. К систематическим относят ошибки, которые входят в результаты измерений по тому или иному закону, как функции источников возникновения систематических ошибок. В практике геодезических измерений применяют следующие способы уменьшения влияния систематических ошибок: 1. устанавливают закон появления систематических ошибок, после чего ошибки уменьшают введением поправок в результаты измерений;

2. применяют соответствующую методику измерений для того, чтобы, например, односторонне действующие систематические ошибки изменяли знак на обратный;

3. используют определённую методику обработки результатов измерений.

Случайные ошибки являются наиболее ярким примером случайной величины. Их закономерности обнаруживаются только в массовом проявлении. Случайные ошибки неизбежны при измерениях и не могут быть исключены из единичного измерения. Влияние их можно лишь ослабить, повышая качество измерений, увеличивая число приемов измерений, а также применяя соответствующую математическую обработку результатов измерений. Причин возникновения случайных ошибок измерений много : влияние внешних условий, неточности изготовления и юстировки приборов, неточности выполнения операций наблюдателем и т.д. Очевидно, что случайные ошибки являются результатом суммирования большого числа независимых элементарных ошибок. На основании центральной предельной теоремы Ляпунова можно считать, что случайные ошибки измерений подчиняются нормальному закону распределения.

3.3 Свойства случайных ошибок измерений

1. Ограниченность: для данного вида и условий измерений абсолютные значения случайных ошибок не превосходят некоторого предела (допуска), т.е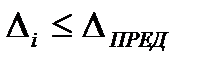

Где 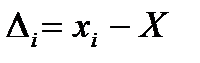- абсолютное значение случайной ошибки, хi – результат измерений, Х- истинное значение измеряемой величины, ∆пред – предел (допуск)

2. Симметричность: при измерениях положительные и отрицательные случайные ошибки встречаются одинаково часто.

3. Плотность: малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

4. Компенсированность: среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений

5. Рассеивание: предел отношения среднего арифметического из квадратов случайных ошибок не равен нулю

6. Пропорциональность: допуск пропорционален стандарту

Если ошибки ряда измерений обладают свойствами с 1 по 6, то их считают случайными.

Предельной ошибкой Δпред называют такую ошибку, больше которой в ряде измерений ошибок не должно быть. В качестве предельных выбирают величины, определяемые по правилу : Δпред=2m (для практических целей) и Δпред=3m (для исследовательских работ) (с вероятностями 0,954 и 0,997 соответственно).

ПОНЯТИЕ О КРИТЕРИЯХ ДЛЯ ОЦЕНКИ ТОЧНОСТИ ИЗМЕРЕНИЙ

Точность измерений – их качество, определяющее близость результатов измерений к точному значению измеряемой величины. Точное значение измеряемой физической величины, если оно не определяется теоретически, неизвестно. В отдельных случаях за точное значение величины может быть принято ее измеренное значение, максимально близкое к истинному значению. В геодезии такие величины называют действительными или исходными. Имея значения Δi истинных или случайных ошибок результатов измерений одной и той же величины, можно получить следующие количественные характеристики точности измерений:

Средней ошибкой называют оценку среднего отклонения v1 (центрального абсолютного момента первого порядка) и вычисляют по формуле: 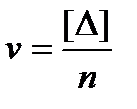это среднее арифметическое из абсолютных значений ошибок

Вероятной ошибкой ϑ* называют оценку вероятного отклонения r. r* — это такое значение случайной ошибки Δ, больше или меньше которого, по абсолютной величине, ошибки являются равновозможными

На практике r* определяется величиной, которую находят, расположив все ошибки Δi в ряд в порядке возрастания их абсолютных величин. Вероятная ошибка r* будет расположена в середине такого ряда.

При нормальном законе распределения случайных ошибок имеют место соотношения:

Предельной ошибкой Δпред называют такую ошибку, больше которой в ряде измерений ошибок не должно быть. В качестве предельных выбирают величины, определяемые по правилу : Δпред=2m (для практических целей) и Δпред=3m (для исследовательских работ) (с вероятностями 0,954 и 0,997 соответственно).

Перечисленные выше критерии Δi , m, ϑ*, r*, Δпред называют абсолютными ошибками; значения абсолютных ошибок получают, как правило, с двумя – тремя значащими цифрами

Относительной ошибкой называют отношение соответствующей абсолютной ошибки к истинному значению измеряемой величины X (если X неизвестно, его заменяют результатом измерения x).

Кроме того, к критериям точности измерений относятся:

• σ – стандарт (основная мера точности результатов геодезических измерений): а) σ определяет величину рассеивания (разброса) отдельных случайных ошибок Δ относительно их среднего арифметического; б) предельное значение случайной ошибки ΔПРЕД. пропорционально стандарту σ. • m – средняя квадратическая ошибка (СКО). В геодезии понятие СКО было введено Гауссом; он же разработал основные положения теории ошибок. На практике при ограниченном числе измерений n СКО одного измерения m вычисляется по формуле Гаусса

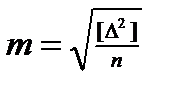
где D = D1 + D2 + D3 +…+ Dn

Для характеристики точности измерений недостаточно указать СКО, также важно установить - по какому числу измерений получено ее значение, т.е. необходимо определить СКО самой СКО

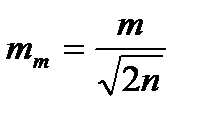
Фактически величина 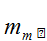позволяет количественно оценить точность замены стандарта на СКО.

Определение средней квадратической ошибки отдельного результата измерений по формуле Бесселя (оценка неизвестного параметра σx): 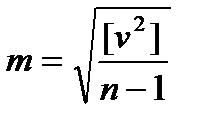, где 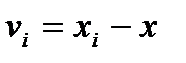- уклонения от арифметической средины. Относится к обработке ряда равноточных измерений.