Размеры некоторых объектов, используемых для определения расстояний 1 страница

Объекты	Расстояние
Высота дома деревянного одноэтажного с крышей Расстояние между столбами линий связи Высота деревянного столба линии связи Высота средневозрастного леса Высота вагона пассажирского многоосного Длина вагона пассажирского многоосного Высота автомобиля грузового Высота человека среднего роста Средняя длина вытянутой руки Средний шаг человека	7—8 м 50(60) м 5—7 м 18—20 м 4,25 м 24—25 м . 2 м 1,6—1,8 м 0,5—0,6 м 0,7—0,8 м
Диаметры'монет:/10 коп.—17 мм; 15 коп.—20 мм; 20 коп.—22 мм; 5 коп.—25 мм L—------------------------ '■' ■;■■-<■'", ,----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 1

§ 20. НАЗЕМНЫЕ СЪЕМКИ. ПЛАНОВЫЕ СЪЕМКИ

Наземные съемкиподразделяются на плановые (горизонталь­ные), высотные (вертикальные) и высотно-плановые (называемые иногда совместными или топографическими). При горизонтальной съемке создается планово-контурное изображение местности без высотной характеристики; в результате вертикальной съемки опре­деляют высоты точек; высотно-плановые съемки обеспечивают изоб­ражение на карте ситуации и рельефа.

Работа, производимая на местности, называется полевой, а обработка полученных данных в лабораторных условиях — каме­ральной.

Плановые съемки.Полевые работы при съемке участка осущест­вляются по основному принципу геодезии — от общего к частному: /сначала создается съемочная геодезическая сеть, а затем произво­дится съемка объектов местности, т. е: подробностей (ситуации).

На начальном этапе проводится ^рекогносцировка — осмотр местности, выбор и закрепление точек съемочной сети. При возможности положение опорных точек «привязывают» к пунктам государственной геодезической сети путем измерения от одного из пунктов расстояния и направления до точки съемочной сети. Од­нако часто положение точек съемочной сети определяется в условной (местной) системе координат.

Затем от точек съемочной сети измеряют расстояния и направле­ния на объекты местности —унимают си т у а ц и ю. В зависимости от того, каким путем определяют направления на объекты, плано­вые съемки подразделяются на утаомер.ные и углоначертательные (графические). При угломерных съемках, горизонтальные углы м¥ж_;. ду направлениями линий и^меряют^угломерными'Ъриб6рГами7"а''при' "графических съемках направления на объекты съемки прочерчивают на горизонтальной плоскости (на бумаге) непосредственно в поле.

\ /

ч

/

ч /

\

/

\

I

/ \

/

*

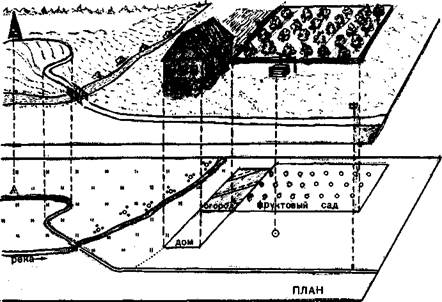
Для изображения на плане взаимного положения и плановых очертаний объектов местности определяют положение их характер­ных точек. При этом количество необходимых точек зависит от размера и конфигурации снимаемых объектов. Положение объектов малой площади, изображаемых на карте внемасштабными знаками, например отдельного дерева, колодца, определяется одной точкой. Для показа прямолинейного предмета (забор, линия связи, улица) достаточно двух точек. Ломаные и криволинейные контуры (дорога, граница угодий, река) изображаются по точкам поворота (рис. 64). По характерным точкам на бумаге вычерчивают контуры объектов, сохраняя геометрическое подобие контурам местности.

Плановое положение объектов получают способами: полярным, засечек, обхода, ординат (промеров), створов. Выбор способа зависит от вида съемки и особенностей снимаемого объекта.

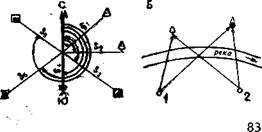
\/При полярном способе (рис 65, Л) положение ряда точек местности определяется расстоянием от известной точки, например пункта съемочной сети, и углом от исходного направления, например магнит-

Рис. 64. Получение планового А изображения местности

Рис. 65. Определение планового положения точек способами-по­лярным (А) и прямой графи­ческой засечки (Б)

, ного меридиана.

1Ш111Н

ПИ111......... IIIIUIIIIIIIIIIIII \i Засечки — способ определения положения на плане третьей точки по двум данным. Засечки подразделяют на прямую и обрат­ную. Прямая засечка (рис. 65, Б) применяется в тех случаях, когда из двух известных точек требуется определить положение недосягае­мой (например, на другом берегу реки или по другую сторону болота и т. п.). От известных точек определяют азимуты направлений на третью точку — при угломерной съемке или прочерчивают их на плане — при углоначертательной съемке, тогда в их пересечении получают искомую точку. Наилучшие результаты получают при угле засечки, близком к 90°. Поскольку этого трудно достичь в полевых условиях, допускается угол засечки в пределах от 60° до 120°. В случае, когда определяемая точка и одна из известных точек доступны для съемщика, но измерение расстояния между ними затруднено, применяют способ обратной засечки. На рисунке 66, А показан участок местности, а на рисунке 66, Б — план этого участка. Положение объектов 2 и 3 имеется на плане, требуется нанести на план изображение объекта /. При углоначертательной способе съемки, стоя в точке 2, прочерчивают на ориентированном плане направление на определяемую точку /, а затем, перейдя с планом в точку /, проводят «на себя» направление от объекта 3. В точке пересечения этих двух линий получают изображение объекта / (рис. 66, В). При угломерной съемке вместо прочерчивания линий измеряют необходимые углы. \/Для съемки дорог в лесу, улиц в селениях и других закрытых контуров пользуются способом обхода. Съемщик передвигается по снимаемой линии (обходит контур) и измеряет длины прямолиней­ных сторон хода и их направления, например азимуты. Вместо азимутов могут быть измерены горизонтальные углы между сторона­ми хода (например, в теодолитной съемке — § 21) или направления этих линий могут быть получены графически путем прочерчива­ния на плане (§ 27). Рис. 66. Нанесение на план объекта 1 (башня) способом обратной засечки. Положе­ние объектов 2 и 3 дано на плане V Способ ординат (промеров) применяется для съемки небольших объектов с криволинейными границами, например участка берега реки, озера, контура рощи и т. п. Вдоль снимаемого контура прокла­дывают съемочный ход или магистраль (АВ) (рис. 67), а затем из ха­рактерных точек контура а, Ь, с опускают перпендикуляры на линию хода. Длины перпендикуляров l\, h, h и т. д., а также расстоя­ния до их основания от началь­ной точки хода So—1, S0-2, So-з и т. д. измеряют одним из спо­собов, рассмотренных в § 15, в зависимости от требуемой точности съемки. Прямолинейные границы объектов или направления от­дельных прямых линий, распо­ложенных под некоторым углом к съемочному ходу, получают ^способом створов. Находясь на линии съемочного хода АВ (рис. 68), можно найти точки пересечения сторон снимаемого объекта с линией хода 1, 2, 3, 4 и из них определить направ­ление нужных линий. Этим спо­собом снимают линии связи и электропередач, заборы, зда­ния, границы пашен и т. п. В зависимости от условий местности и особенностей ситуа­ции при плановых съемках ис­пользуют обычно несколько спо­собов. § 21. ТЕОДОЛИТНАЯ СЪЕМКА Плановая (горизонтальная) теодолитная съемка относится к угломерному виду съемок, при котором на местности измеряют расстояния лентой и дальноме­ром и горизонтальные углы с помощью теодолита. Обычно применяется в равнинной мест­ности для съемки населенных пунктов, застроенных участков и пр. Горизонтальный угол р ле­жит в горизонтальной плоско­сти, его лучами служат гори­зонтальные проекции направле­ний на наблюдаемые объекты (рис. 69).   О О ., •. L О ...... U -^ 8М г     So-з                   Рис. 67. Измерения при съемке способом ординат Рис. 68. Визирование с точек магистрального хода по створу Рйс. 69. Принцип .измерения горизонталь­ных углов. Заштрихованы вертикальные плоскости, проходящие через точку уста­новки инструмента (вершина измеряемого угла) и визируемые предметы                               Применяемые приборы. Теодолит— геодезический инструмент для определения направлений и измерения горизонтальных и верти­кальных углов при топографо-геодезических работах. Его основной рабочей частью служат горизонтальный и вертикальный круги с градусными и более мелкими делениями. Применяются приборы с металлическими и, главным образом, со стеклянными кругами. Последние снабжены оптическими отсчетными устройствами и назы­ваются оптическими теодолитами. Современные теодолиты весьма разнообразны по конструкции, точности результатов измерений, массе. Однако основные узлы в разных теодолитах имеют много общего. Рис. 70. Теодолит с металлическими кругами Рис. 71. Схема устройства теодолита Рассмотрим устройство одного из теодолитов, внешний вид кото-. рого показан на рисунке 70, а разрез дан на рисунке 71. Прибор, подобно другим геодезическим инструментам, устанавливается на штативе с помощью массивной подставки А, снабженной подъем­ными винтами / для приведения вертикальной оси инструмента в от­весное положение. Становой винт 2 соединяет подставку с треногой. Во втулку 3 входит ось вращения 4. Основные части теодолита: горизонтальный круг В с круговой шкалой-лимбом, алидадный круг С, зрительная труба D и вертикальный круг Е. Круг В служит для измерения горизонтальных углов, на его лимбе нанесены деления, цена которых 20' (рис. 72). Деления подписаны через 10° по ходу часовой стрелки от 0° до 350°. Ось горизонтального круга 4 может вращаться во втулке подставки 3. Ось алидадного круга 5 входит во втулку горизонтального круга В. Таким образом, оси вращения Рис. 72. Шкала верньера и часть лимба ■■^: Рис. 73. Схема отсчета по верньеру: / — цена деления лимба; v — цена деления вернье­ра; ( -^ точность верньера, ( = / — v. Совпадающие штрихи утолщены и отмечены треугольничком обоих кругов совпадают. На двух концах диаметра алидадного круга нанесена шкала для отсчитывания по лимбу, называемая верньером. Чтобы исключить при отсчетах влияние эксцентритета круга и алидады, среднюю величину отсчета вычисляют по парным отсчетам, взятым по обоим верньерам алидады. Верньер служит для измерения углов с большей точностью, чем цена деления лимба1. Он представляет собой дугу, разделенную на равные части, число которых на единицу больше числа делений лимба, захватывающих ту же дугу. Следовательно, если обозначить цену деления лимба, выраженную в угловых мерах, буквой /, цену деления верньера (также в угловых мерах) — v, число этих делений лимба (л— 1), а верньера — п, то можно составить равенство / (п—\) = vn или In— l = vn\ откуда In — vn = l; n(L—v)=l. Обозна­чив (l — v) через t, назовем ее точностью верньера, получим: / =—. Таким образом, точность верньера равна цене деления лимба, деленной на число делений верньера. Пользуясь этой формулой, определяют точность верньера теодолита. Если цена деления лимба 20' 20' и на верньере 40 делений, то точность верньера /= — =0,5', т. е. / = 30". Рассмотрим по схематическому изображению верньера на рисунке 73, как производится отсчет с его помощью. На рисунке показаны участки дуг верньера и лимба в разных взаимных положениях. В первом случае (А) ноль верньера совпадает (сливается) со штрихом 30 на лимбе, следовательно, отсчет по лимбу равен 30°. На втором рисунке (Б) показано, что ноль верньера сместился на дугу, равную одной точности верньера; при этом первый штрих верньера совпал (слился) с каким-то штрихом лимба. Наконец, на нижнем рисунке (В) ноль верньера сместился на дугу, равную 2<, и при этом второй штрих верньера совпал с каким-то штрихом лимба. Отсюда ' Теория измерительного устройства разработана X. Клавдием в конце XVI в., а само устройство названо нониусом в память учителя П. Нониуса. В начале XVII в. П. Вернье усовершенствовал нониус и соединил его с подвижной алидадой. Это приспособление под названием верньер практически без изменений дошло до наших дней.                                   следует.^что для оценки величины дуги некоторой части одного деления лимба а надо найти номер штриха верньера п,, совпадающего с каким-то штрихом лимба и умножить на точность верньера t, т. е. a = n.\t. Для отсчитывания по кругам данного теодолита используют лупы, а в оптических теодолитах — шкаловые микроскопы и опти­ческие микрометры. Полный отсчет по лимбу А складывается из отсчета Л,, по основ­ному кругу от 0 лимба до 0 верньера и отсчета по верньеру А = — Ai-\-a. На рисунке 74 полный отсчет равен 53°33'30". Алидадный круг прикрыт кожухом, в котором над верньерами имеются окна. К кожуху прикреплены два цилиндрических уровня 6 с помощью которых лимб приводят в горизонтальное положение' а вертикальную ось инструмента — в отвесное. На рисунке 71 пока­зан один уровень, так как второй не попал в плоскость чертежа К кожуху алидады крепятся подставки 7, поддерживающие -ось вращения 8 зрительной трубы D и вертикального круга Е. Зрительная труба геодезических инструментов служит визирным устройством, с помощью которого производится точное наведение на предмет (веху, рейку). Поскольку рассматриваемые предметы обычно удалены на значительные расстояния, зрительные трубы устроены по астрономическому типу (рис. 75). Труба состоит из объектива и окуляра, расположенных так что задний фокус объектива почти совпадает с передним фокусом окуляра. Объектив дает действительное, обратное и уменьшенное изображение объекта АВ в виде А'В'. Изображение А'В' рассмат- К,?ТоЯ В окуляР' что дает Увеличенное, обратное изображение л а . Ввиду того что расстояния до реек А В при съемках меняются и изображение А'В' перемещается в трубе, необходимо фокусировать трубу по предмету, что достигается перемещением внутренней линзы (рис. 76). Трубы современных геодезических инструментов дают увеличение от 15-х до 50-х (даже 65—80-х в высокоточных при­ борах). г Зрительная труба снабжена сеткой нитей, предназначенной для точного визирования. Это два тонких взаимно перпендикулярных штриха, награвированных на прозрачной пластинке (на рис. 76 обозначены 1—1 и 2—2), закрепленной вблизи переднего фокуса окуляра. Воображаемая линия, проходящая через центр сетки нитей и оптический центр объектива, называется визирной осью, а ее Рис. 74. Отсчет по лимбу и верньеру: 53°33'30" продолжение к предмету — визир­ным лучом. При визировании рей­ку фокусируют перемещением внутренней линзы, изображение сетки — перемещением окуляра, затем центр сетки нитей совмеща­ют с видимой в трубу заданной точкой. Геодезические инструменты   А Объектив В"в' Окуляр   ^Гр-^^А-_________ " "1*1 nS'-5 - В s&^№^= -JjJ XU>?     r^v Рейка Ш Рис. 75. Ход лучей в зрительной трубе Рис. 76. Схематический разрез зри­тельной трубы с внутренним фокуси­рованием (А): S=17m 1=17 см 1—объектив; 2— окулятор; 3 — сетка нитей; 4 — дополнительная линза. Основные визирные нити сетки (Б): 1 — 1; 2—2 Рис. 77. Некоторые виды реек для измерения расстояний с помощью дальномеров геометрического типа. Поле зрения трубы при визировании на рейку оснащены дальномерными устройствами, сконструированными раз­лично в высокоточных приборах и инструментах технического на­значения. В последних применяется нитяной дальномер, являющийся дальномером с постоянным углом. В этих приборах на прозрачной пластине в трубе, кроме двух основных нитей, предназначенных для точного визирования, нанесены дополнительно две горизонтальные нити (а и b на рис. 77). В наблюдаемой точке устанавливают дальномерную рейку в виде деревянного бруса длиной 3—4 м с равностоящими делениями. Типы дальномерных реек показаны на рисунке 77. Измеряемое расстояние пропорционально числу делений реки, видимых между дальномерными нитями. Обратимся к рисунку 78. Пусть О — оптический центр объекти­ва, точка F — передний фокус объектива, f — его фокусное расстоя­ние, отрезок ab — расстояние между дальномерными нитями на сет­ке, б — отрезок трубы от оси ее вращения ZZ до объектива. Положим, что измерение линии ведется на равнинной местности и визирный луч почти перпендикулярен к рейке R, установленной в определяемой точке. При визировании на рейку параллельные лучи, проходящие через нити а и Ь, пересекутся в переднем фокусе и спроектируются на рейке в точках А я В; часть, рейки, видимую между этими нитями, обозначим буквой /. Расстояние от инструмента до рейки S = Si + f + 6. Для каждого прибора сумма f + 6 = c = = const — величина постоянная, называемая постоянной дально­мера. Из подобия треугольников a'b'F и ABF вытекает, что -г-=—; П S откуда Si= -1—. Отношение/:ab = Кявляется постоянной величиной, называемой коэффициентом дальномера. Поэтому формула в целом примет вид S = A7 + c. Эта формула применяется при измерении расстояний дальномером в равнинных районах с небольшими углами наклона. При съемках в масштабе 1:10 000 и мельче величиной с можно пренебречь, поскольку она весьма мала (40—60 см) и в масштабе плана будет меньше графической точности, и тогда расстояние S = Kl. В приборах обычно К= 100, вследствие чего один сантиметр на рейке соответствует одному метру на местности. Так, например, если при измерении расстояния на рейке между дальномерными нитями 17 см, то это соответствует 17 м на местности (рис. 77). Нитяные дальномеры служат для измерений расстояний до 300 м. Точность измерений составляет—- — — от длины линии, т. е. ниже, чем при измерениях лентой. Поэтому при создании опорной съемоч­ной сети длины сторон хода измеряют мерной лентой, а дальномер используют для съемки подробностей, а также при проведении тахеометрической съемки (см. § 27). Рис. 78. Ход лучей в нитяном дально- Рис. 79. Оптический шкаловый теодолит мере (А). Вид сетки нитей (Б) Вертикальный круг теодолита применяется для измерения углов наклона при тригонометрическом нивелировании (§ 25).   В     3'     1_ 1 1 1 1   llll               1 1 ~гг                           Буссоль теодолита служит для определения магнитных азимутов направлений. ш Исправный теодолит должен отвечать ряду требований, а имен­но: 1) ось уровня на алидаде го­ризонтального круга должна быть перпендикулярна главной оси ин­струмента; 2) ось вращения трубы должна быть перпендикулярна к визирной оси трубы; 3) ось враще­ния трубы и главная ось должны быть взаимно перпендикулярны. Поскольку эти условия могут на­рушаться в результате перевозок инструмента и его длительного ис­пользования, необходимо перед началом полевой работы произво­дить поверки теодолита. Рис. 80. Поле зрения отсчетного штрихового микроскопа оптиче­ского теодолита: отсчетный штрих. В — лимб вертикаль­ного круга, Г — лимб горизонтального круга. Цена деления лимбов 10'. От­счеты по лимбам: вертикального круга 358°06', горизонтального круга 23°38' В оптических теодолитах (рис. 79) изображение шкал с горизон­тального и вертикального стеклян­ных кругов передаются в отсчет-ный микроскоп, расположенный вблизи окуляра (рис. 80). Благо­даря этому повышается точность измерений и убыстряется работа, так как наблюдатель сразу после наведения берет отсчет по обоим кругам, не отрывая глаза от трубы. В теодолите Т-30 средняя квадра-тическая погрешность измерений угла равна 30". Теодолит Т-ЗОМП (модификация теодолита Т-30) снабжен компенсатором при вер­тикальном круге и зрительной тру­бой прямого изображения. Рис. 81. Схема измерения угла по гори­зонтальному кругу теодолита (вид сверху). Отсчеты по лимбу: а — при визировании на правую точку Л, b — при визировании на левую точку В. Z.ACB = Для измерения гори­зонтального угла инстру­мент на штативе устанавливают в вершине измеряемого угла, при­водят горизонтальный круг в го­ризонтальное положение по уров­ням, центрируют над точкой с большой точностью (по отвесу или наблюдая точку через вертикально установленную зрительную трубу, объективом вниз, у приборов с полой осью алидады). При закрепленном круге поворотом алидады наводят трубу (вертикальную нить сетки) на правое направление и берут отсчеты по обоим верньерам, получают средний отсчет а\ (рис. 81); затем, не открепляя круга, визируют левое направление и получают отсчет Ь\. Так как деления на лимбе идут по ходу ча­совой стрелки, отсчет щ будет больше отсчета Ь\ и измеряемый угол имеет величину Pi=ai — b\. Эти действия составляют первый полуприем. Если визирование проводилось при положении верти­кального круга справа от наблюдателя, оно называется визирова­нием при «круге право» (КП), если круг был слева — визирование при «круге лево» (КЛ). Одного полуприема недостаточно, для контроля проводится второй полуприем — при другом положении вертикального круга. Зрительную трубу переводят через зенит (объективом вниз), горизонтальный круг поворачивают приблизительно на 90° и при этом положении вновь проводят те же операции, что и при первом полуприеме, получают второе значение угла ^2 = ^2 — Ь2. Из двух значений при их допустимом расхождении не более 1' вычисляют среднюю величину угла н 2 " Так осуществляется полный прием, в результате применения кото­рого исключается влияние остаточных погрешностей из-за непер­пендикулярности визирной и горизонтальной осей трубы и непер­пендикулярности горизонтальной оси трубы и вертикальной оси инструмента. Точность измерения угла тридцатисекундным теодоли­том составляет около 0,5'. Опорная съемочная сетьпри теодолитной съемке создается обычно прокладкой замкнутых ходов (полигонов). Положение опорных точек, которыми являются поворотные точки хода, зависит от конфигурации и размеров снимаемого участка. Длины сторон хода измеряют мерной лентой дважды, при этом разница обоих измерений не должна превышать 1:2000 от длины линии. Если линии имеют на местности наклон более 1,5°, измеряют угол наклона и вводят поправку за приведение длин линий к горизонту. В полигоне Рис. 82. А. Измерения при прокладке теодолитного полигона на местности. Б. Вычисление дирекционного угла сторон полигона по значению дирекционного угла предыдущей стороны и углу между предыдущей и последующей сторонами n.L =rr -l_1Sn°_R апосл. — апред. ± 180° — Р измеряют способом приемов внутренние углы — правые при движе­нии по часовой стрелке (рис. 82). Данные полевых измерений: номера точек установки теодолита (станций) и визируемых точек, значения отсчетов при правом КП и левом КЛ положении вертикального круга, средние значения отсчетов и вычисленные значения углов, длины и азимуты сторон хода тщательно фиксируют в полевом журнале (табл. 9). Таблица 9 Журнал измерения горизонтальных углов теодолитом и длин сторон полигона

Лентой

№ точек	Отсчеты по верньерам	Угол	Средний угол	Магнит­ные азимуты	Длины линий, м	Углы наклона
стоя­ния	визи­рова­ния	I	и	средний
		кп 218°40' 104°18' КЛ 40°51' 286°26'	41'-17' 51' 27'	218°40,5' 104°17,5' 40°5Г 286°26,5'	114°23,0' 114°24,5'	114°23,75'	126° 11,5°	линия 2—3 71,86 Ср. 71,83	Г 30'

Примечание. Точка визирования 1 — правая, точка 3 — левая.

При вычислении угла по отсчетам при КЛ к 40°5Г был прибавлен период: (40°51' + 360°) — 286°26,5'= 114°24,5'

В замкнутом полигоне теоретическая сумма внутренних углов 2_те0р.= 180° (я —2), где п — число углов.

Фактически полученная в результате измерений сумма углов — 2_факт обычно отличается от теоретической на величину угловой невязки /« = Е_факт — 2_теор.

Предельная допустимая ошибка в углах полигона вычисляется

по формуле fp ⁼~7rt У^> ^гД^{е п} — число углов, t — точность вернье­ра. Если угловая невязка получится больше допустимой, необходимы повторные измерения. Если результаты удовлетворительны, получен­ную невязку /р делят на число углов п, в каждый угол вводят по-

правку б = ^пред' со знаком, обратным знаку невязки, и получают ис­правленное значение угла р.

P = Pi±6, где Pi — измеренная величина угла.

Съемка подробностейосуществляется с точек опорной сети (со станций), где поочередно устанавливают теодолит. Съемка ведется главным образом способами полярным, ординат и засечек (§ 20). В первом случае в точки, подлежащие нанесению на будущий план, выставляется поочередно дальномерная рейка. Эти точки называются пикетами. Со станции на каждый пикет определяют

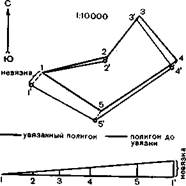
Графическое определение величины поправок Масштаб длин сторон полигона 1: 20 ООО Рис. 83. Графический способ определе­ния поправок в длины сторон замкнуто­го полигона

расстояние по дальномеру и направление по горизонтальному кругу и по буссоли. Результаты полевых наблюдений фиксируют в журнале и на абрисе, представляющем схематическую зарисовку снимаемого участка условными знаками.

Камеральные работывключают вычислительную обработку поле­вых данных и построение плана. При обработке сравнивают изме­ренные величины с теоретическими, выявляют невязки, вводят поправки. Затем вычисляют дирекционные углы сторон хода, зная, что дирекционный угол последующей стороны a₂-3 = ai-2+ 180° — fb (см. рис. 82).

По дирекционным углам и длинам сторон теодолитного хода строят план полигона с помощью транспортира, циркуля-измерителя и поперечного масштаба. При этом возможно несовпадение на плане начальной и конечной точек замкнутого хода, возникшее вследствие накопления погрешностей измерений и графических построений, так называемая линейная невязка полигона. Если не­вязка не превышает допустимой величины, равной 1:300 от длины хода, ее устраняют способом параллельных линий, как показано на рисунке 83.

Здесь тонкими линиями вычерчен план полигона, полученный при первоначальном построении. Конечная точка Г при этом не совпала с начальной точкой 1, т. е. возникла линейная невязка хода — отрезок Г —1. Допустимую невязку распределяют пропор­ционально длинам сторон полигона. Распределение невязки произ­водят графически, путем построения треугольника увязок (рис. 83). Для этого на прямой линии откладывают последовательно длины всех сторон хода (обычно в более мелком масштабе, чем основной план). В конечной точке хода Г восстанавливают перпендикуляр

и на нем откладывают величину

ПЛАН ПОЛИГОНА

- —j невязки в масштабе основного плана. Конец перпендикуляра со­единяют прямой с первой точкой хода.

Из точек хода 2, 3, 4, 5 вос­станавливают перпендикуляры до пересечения с гипотенузой тре­угольника, длины которых равны величине увязок в соответствую­щих точках хода на плане. Поли­гон увязывают путем перемещения его вершин на эти отрезки парал­лельно направлению сдвига конеч­ной точки хода. Утолщенными ли­ниями (рис. 83) показан план полигона после увязки.

Ситуацию наносят на план по данным журнала и абриса, изме­ряя углы направления транспорти­ром и расстояния от опорных точек

до пикетов и применяя условные топографические знаки.

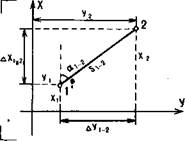
Рис. 84. Определение прямоугольных координат конечной точки (2) пря­мой линии по известным координа­там начальной точки Xt, Y\, дирек-ционному углу этой прямой ai-2 и ее горизонтальному проложению S,_2

При построении планов большей точности опорные пункты и объекты ситуации наносят по прямо­угольным координатам, используя предварительно построен­ную прямоугольную координатную сетку. Координаты точек вычисляют по координатам начальной точки Х\ и У! и приращениям координат AXi_2j ДУ,_₂; Х₂ = Х_{+ЬХ_{_₂; У₂=У,+ + ЛУ1_₂ (рис. 84). Приращения ко­ординат выбирают из специальных таблиц по углу и расстоянию или вычисляют по формулам: