Способ, основанный на использовании Правил Непера

Выделим на единичной сфере (см. Рис.3.4) два сферических треугольника: 1-2-3 и 3-4-5. При этом отметим, что углы 1 и 5 являются прямыми.

Для треугольника 1- 2 -3, можем составить схему (см. Рис. 3.5); тогда, используя Первое Правило Непера, имеем:

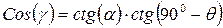. (3.3)

Тогда

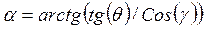, (3.4)

и кардановая погрешность по углу тангажа примет вид:

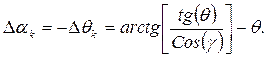(3.5)

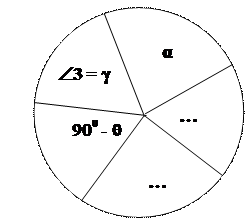
Рис.3.5.

Для треугольника 3 – 4 – 5, схема имеет вид, показанный на Рис.3.6.

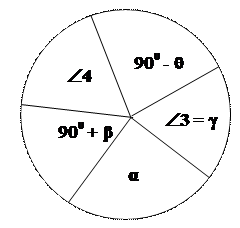
Рис.3.6.

Тогда, используя Второе Правило Непера, получим

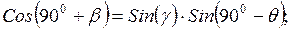(3.6)

и по углу крена можно записать следующие соотношения:

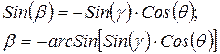(3.7)

Следовательно, погрешность по углу крена есть

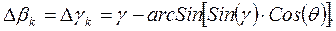(3.8)

Способ, основанный на решении матричных кинематических уравнений

Определим связь между системами координат (см. рис.3.7).

Здесь

σ, τ – углы ориентации вектора кинетического момента гировертикали относительно путевой системы координат, т.е. углы отклонения от вертикали места.

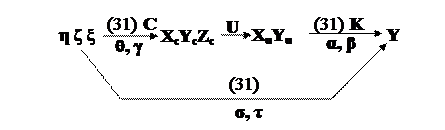
Рис.3.7.

При этом будем, для простоты примера, полагать что системы горизонтальной коррекции гировертикали обеспечивают ориентацию вектора кинетического момента по вертикали места идеально, т.е. углы σ, τ равны нулю (т.к. рассматриваются только кардановые погрешности).

Следовательно, кинематическое уравнение в матричной форме согласно схеме связи между системами координат (см. рис.3.7.) примет вид:

(3.9)

Где

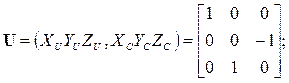(3.10)

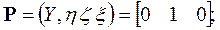(3.11)

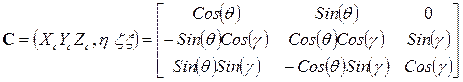; (3.12)

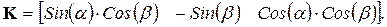(3.13)

Или после простейших преобразований

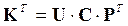. (3.14)

Раскрывая это уравнение, получим

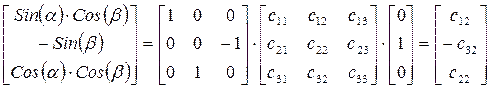; (3.15)

или

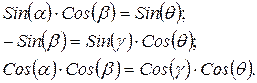(3.16)

Следовательно, кардановая погрешность может быть записана в хорошо известном [5, 10] виде:

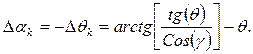(3.17)

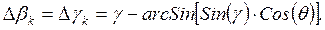(3.18)

Способ, основанный на использовании проекций вектора кинетического момента

Определим проекции вектора кинетического момента, но используя два подхода:

– находим проекции вектора кинетического момента на оси связанной системы координат используя только угловые координаты летательного аппарата: 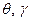(по рис.3.4.);

– находим проекции вектора кинетического момента на оси связанной системы координат используя только углы поворота гироузла: 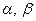(по рис.3.4.);

Т.е. имеем

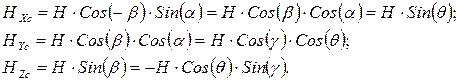(3.19)

Тогда очевидно получим выражения, аналогичные тем, которые были получены ранее другими способами:

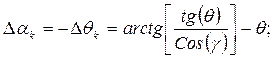(3.20)

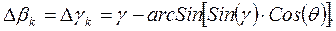(3.21)

Уравнения погрешности работы гироскопической вертикали

Введение.

Рассмотрим способ составления уравнений на примере рассмотренной выше гировертикали, базовая схема которой показана на Рис.3.8.

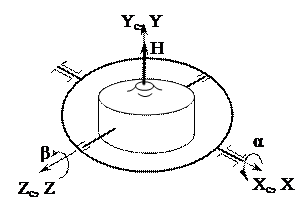
Рис.3.8. Базовая схема гировертикали.

Связь между системами координат, используемых в данной задаче, показана на Рис.3.9. Где

X_gY_gZ_g – географическая система координат;

X_pY_pZ_p – путевая система координат;

X_сY_сZ_с – связанная система координат;

XYZ – система координат Резаля.

Ψ, θ, γ – углы ориентации ЛА (углы курса, тангажа и крена);

α, β – углы ориентации гироузла (углы поворота наружной рамы и угол поворота гироузла соответственно);

σ, τ – углы ориентации вектора кинетического момента относительно путевой системы координат.

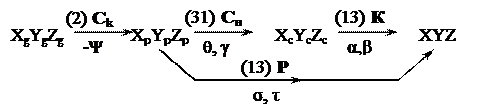
Рис.3.9. Схема связи между системами координат.

Согласно определению матрицы ориентации имеют вид:

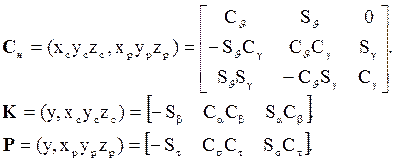(3.22)

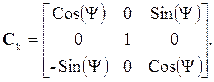(3.23)

Здесь использовано сокращенная форма записи тригонометрических функций:

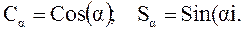(3.24)

Очевидно

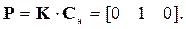(3.25)

Идеальный режим.

Рассмотрим в начале случай 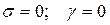, т.е. вектор кинетического момента гировертикали во время движения ЛА точно совпадает с вертикалью места. Тогда имеем кинематическое уравнение, записанное в матричной форме, в виде

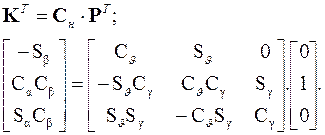(3.26)

Или в форме системы уравнений:

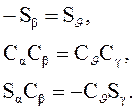(3.27)

Тогда очевидно решение этой системы есть

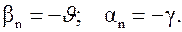(3.28)

Следовательно, в идеальном режиме углы ориентации гироузла (принадлежность к идеальному режиму отмечена индексом «n») относительно связанной системы координат (корпуса прибора) есть углы ориентации ЛА (с обратным знаком) соответственно.

Общий режим.

Рассмотрим теперь общий случай 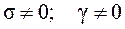, т.е. когда вектор кинетического момента гировертикали не совпадает с вертикалью места на углы σ и τ соответственно. Естественно полагать эти углы (это отклонение) достаточно малыми, т.к. они характеризуют погрешность работы гировертикали.

Введем следующие обозначения:

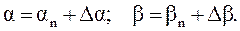(3.29)

где так же имеет место малость погрешности, выраженная через углы ориентации гироузла:

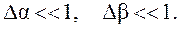(3.30)

Кинематическое уравнение в этом случае примет вид

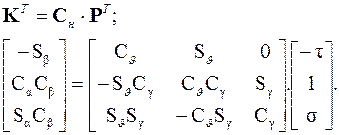(3.31)

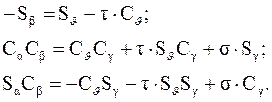(3.32)

Учитывая 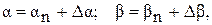получим связь между параметрами σ, τ и Δγ, Δθ:

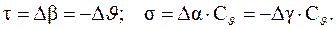(3.33)

Таким образом

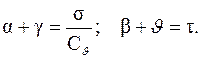(3.34)