Определение абсолютных линейных скоростей и ускорений места установки измерительных устройств
Согласно кинематической схеме (см. рис.1.) можем записать:
 . (4.12)
. (4.12)
Или с учетом соотношений ( ), получим:
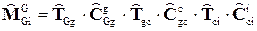 . (4.13)
. (4.13)
Где
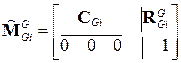 . (4.14)
. (4.14)
С помощью матриц

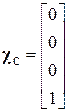 , (4.15)
, (4.15)
можно из однородной матрицы перемещения выделить
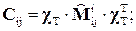
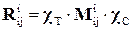 . (4.16)
. (4.16)
Согласно правилам перемножения матриц и выделения искомых матриц, имеем:
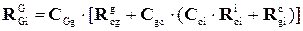 . (4.17)
. (4.17)
Таким образом, для получения абсолютной линейной скорости необходимо определить
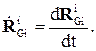 (4.18)
(4.18)
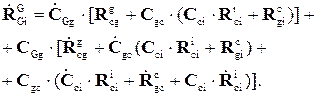 (4.19) Учитывая соотношения
(4.19) Учитывая соотношения
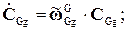
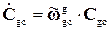 ;
;  ; (4.20)
; (4.20)
или
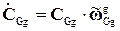 ;
; 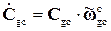 ;
; 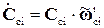 . (4.21)
. (4.21)
Тогда имеем:
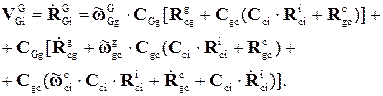 (4.22)
(4.22)
Обычно абсолютная скорость движения исследуемой точки необходимо выразить в проекциях на оси установочной системы координат, т.е.
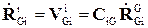 . (4.23)
. (4.23)
Т.о., вектор абсолютной линейной скорости места установки измерительных устройств, выраженный в проекциях на оси установочной системы координат, имеет вид:
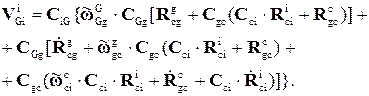 (4.24)
(4.24)
Или
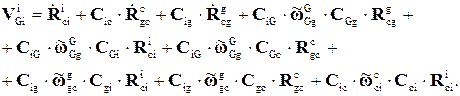 (4.25)
(4.25)
Учитывая соотношения

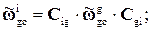
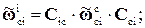 (4.26)
(4.26)
получим окончательно
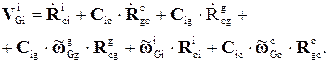 (4.27)
(4.27)
Для того, чтобы получить выражение для абсолютного линейного ускорения, необходимо вычислить
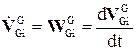 . (4.28)
. (4.28)
Т.е.

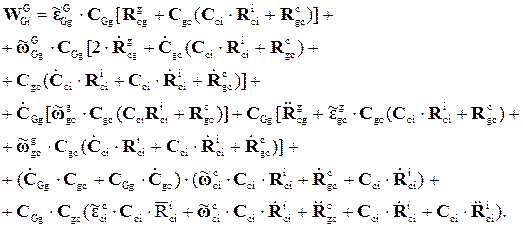 (4.29)
(4.29)
Запишем полученный результат в матричной форме
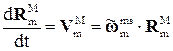 , (4.30)
, (4.30)
Индекс “~ (тильда)” указывает на кососимметричную форму данной матрицы.
В традиционной форме угловую скорость можно представить в виде
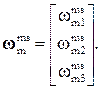 (4.32)
(4.32)

где 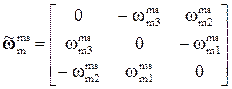 (4.31)
(4.31)
Пример: абсолютные угловые скорости и линейные ускорения места установки блока датчиков.
Постановка задачи
Измерительный блок, состоящий из трех датчиков угловой скорости и трех акселерометров, входные оси которых соответственно направлены по ортогональным осям: OdXd1iYd1iZd1i (i=1, 2, 3.) – для датчиков угловой скорости (ДУС) и OdXd2iYd2iZd2i (i=1, 2, 3.) – для датчиков линейного ускорения (АКС). Следует отметить, что измерительный блок установлен на существенном удалении его от центра масс ЛА, а входные оси датчиков, как правило, не параллельны направлениям осям связанной системы координат ЛА.
В качестве параметров угловой ориентации ПО в работе использованы следующие параметры:
· кардановы углы (углы ортогональных поворотов) – угол курса, угол тангажа и угол курса ЛА;
· направляющие косинусы – компоненты матрицы (в форме Литвин – Седого);
А также однородные параметры, позволяющие задавать как угловые, так и линейные перемещения рассматриваемых систем координат.
Связь между используемыми системами координат представлена на Рис.1.; в качестве параметров, определяющих расположение систем координат между собой, использованы, так называемые, однородные параметры в матричной форме.
Вместо одновременного рассматривания двух систем координат датчиков ДУС и АКС соответственно, пока будем рассматривать только одну (любую) из них, которую обозначим OdXdYdZd.
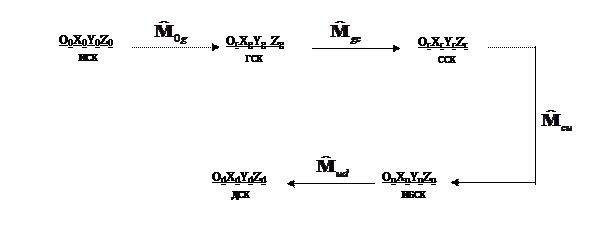
Рис.1. Системы координат
Тогда положение системы координат датчиков относительно инерциальной системы координат определяется следующим соотношением
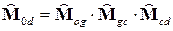 . (1.1)
. (1.1)
Где матрицы положения, определяющие ориентацию промежуточных систем координат, имеют вид: 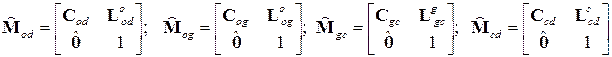 .
.
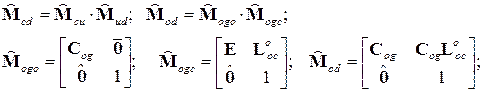
Здесь использованы следующие матрицы-вектора параметры положения:
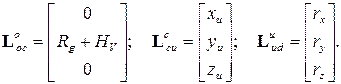 (1.2)
(1.2)
 - координаты места установки измерительного блока на борту ЛА;
- координаты места установки измерительного блока на борту ЛА;
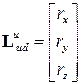 - координаты места установки прибора в измерительном блоке ;
- координаты места установки прибора в измерительном блоке ;
HV – высота полета ЛА.
Выполнив следующие очевидные преобразования,

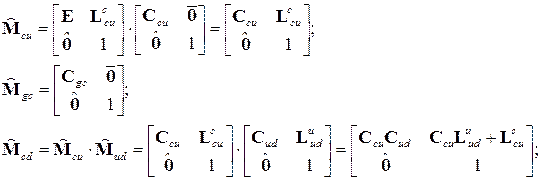
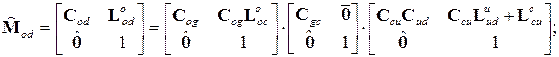
получим выражение для матрицы, определяющей положение системы координат датчиков относительно инерциальной системы координат

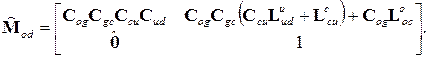 (1.3)
(1.3)
Следовательно, переходя к традиционной форме задания ориентации и положения системы координат датчиков относительно инерциальной системы координат, получим:
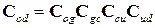 ; (1.4)
; (1.4)
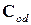 - матрица направляющих косинусов, определяющая угловую ориентацию системы координат датчиков относительно инерциальной системы координат;
- матрица направляющих косинусов, определяющая угловую ориентацию системы координат датчиков относительно инерциальной системы координат;
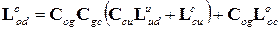 ; (1.5)
; (1.5)
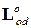 - матрица-вектор, определяющая положение начала системы координат датчиков относительно инерциальной системы координат.
- матрица-вектор, определяющая положение начала системы координат датчиков относительно инерциальной системы координат.
