Уравнивание (увязка) приращений координат теодолитного хода

Необходимость такого уравнивания возникает в связи с погрешностями, возникающими, как правило, при выполнении линейных измерений. При уравнивании необходимо выполнить следующие действия:

- определить невязки по осям абсцисс и ординат, абсолютную и относительную линейные невязки, т.е.

f_AX=П-Т,

f_AY=П-Т,

где П - практическая сумма измеренных углов,

Т - теоретическое значение горизонтальных углов.

f_абс =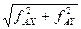

f_отн= f_абс /Sd

- оценить полученную невязку сравнением с допустимым значением;

f_отн < 1/2000;

- ввести поправки в уравниваемые величины с обратным знаком знаку невязки и прямо пропорционально горизонтальным проложениям с округлением до 0, 01м;

- выполнить контроль уравнивания:

а) сумма поправок должна быть равна величине невязки с обратным знаком,

б) сумма исправленных значений должна равняться теоретическому значению.

9-11.Вычислительная обработка теодолитных ходов. Сущность обработки – вычисление координат точек теодолитного хода по заданным a₀ , a_n, Х₁, У₁, Х_n, У_n опорных линий и точек в начале и конце хода и по измеренным горизонтальным углам b и длинам сторон d. Порядок вычислений:

1.Уравнивание горизонтальных углов. Вычисляют невязку в углах f_b

как разность между суммой измеренных углов b_i и теоретической суммой: f_b = åb_i - åb_теор.

По теории геометрии для полигонов åb_теор = 180⁰ (n –2), для разомкнутых ходов по правым углам поворота åb_теор = a₀ - a_n + 180⁰ n. Подставив в f_b , получим:

f_b = åb_i – 180⁰ (n – 2) - для полигонов, f_b = åb_i – 180⁰ n + a_n - a₀ - для разомкнутых ходов.

Допустимая невязка : доп.f_b = 1¢ Ö n из расчета предельной погрешности измерения горизонтальных углов 1’ согласно СНиПу; n – число углов.

Если f_b £ доп. f_b , то вычисляют уравненные углы: b_{i ур} = b_i - f_b / n. Контроль: åb_{i ур} = åb_теор 2. Вычисление дирекционных углов: a_i = a_i-1 + 180⁰ - b_{i ур} - дирекционный угол последующей

линии равен дирекционному углу предыдущей линии плюс 180⁰ и минус уравненный угол, правый по ходу. Формула вытекает из решения плановой задачи: «Вычисление дирекционных углов смежных сторон». Контроль вычислений – получение a₀ в полигоне и a_n в разомкнутом ходе.

3. Вычисление и уравнивание приращений координат. Приращения координат вычисляются по формулам прямой геодезической задачи :Dx_i = d_i cosa_i , Dy_i = d_i sina_i где d_i – горизонтальное проложение i –овой линии.

Согласно теореме геометрии «сумма проекций сторон многоугольника на любую ось равна нулю» можем записать для полигона åDх_теор = åDу_теор = 0. Для разомкнутого хода åDх_теор = X_n – X₁ , åDу_теор = У_n – У₁ . Откуда невязки по осям координат: f_x = åDх_i, f_y = åDу_i - для полигонов,

f_x = åDх_i – ( X_n – X₁ ) , f_y = åDу_i -(У_n – У₁ ) - для разомкнутых ходов.

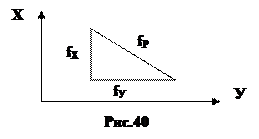Невязка в периметре хода f_pв соответствии с рис.40 будет равна f ²_p = f ²_x +f ²_y .

Допустимая невязка в периметре хода вычисляется по формуле доп.fP = (1/N) / P , где 1/N - нормативная точность линейных измерений, Р = ådi - периметр хода. Так, при строительстве до 5 этажей принимается 1/N = 1/2000. Если fP £ доп.fP , то вычисляют уравненные прнращения координат по формулам Dxi ур=Dxi - fx di / P, Dyi ур= Dyi – fy di / P . Контроль вычислений: : åDхi ур =åDхтеор , åDуi ур = åDутеор .

.

Примечание. Погрешности измерения горизонтальных углов не зависят от их величин. Углы 10⁰ и 300⁰ измеряются одинаково точно. Поэтому невязки f_b распределяются на измеренные углы поровну. Погрешности измерения длин линий зависят от их величин. Чем больше длина линии, тем больше погрешность. Поэтому невязки f_x и f_y распределяются на вычисленные приращения прямо пропорционально длинам линий.

4. Вычисление координат точек: Х_i = X_i-1 + Dx_{i ур} , У_i = У_i-1 + Dy_{i Ур} - координата последующей точки равна координате предыдущей точки плюс уравненное приращение между ними.

12. Виды плановых опорных геодезических сетей, назначение государственной геодезической сети, её классы по точности. Высотные геодезические сети, их классы по точности, назначение.

Геодезические сети подразделяются:

• по виду определяемых координат - плановые и высотные;

• по виду построения - триангуляция, полигонометрия, трилатерация и их сочетания;

• по назначению - государственные, сети сгущения и сети съемочного обоснования, сети специального назначения.

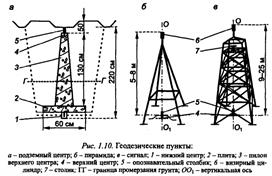
Назначение: государственная геодезическая сеть создается для распространения на всю территорию страны единой системы плановых координат и высот. Эта сеть представлена геодезическими пунктами, закрепленными на местности (рис. 1.10, а).

Носителем координат геодезического пункта служит метка в металлической пластине верхнего центра 4, которая заложена в пилоне - подземном центре пункта. Верхний центр дублируют нижним центром 1, который заложен на дне котлована под плитой 2. Глубина заложения нижнего центра - не менее 2 м. После закладки центр окапывают и устанавливают опознавательный столбик. Над центром строят металлическую пирамиду (рис. 1.10, б) или высокий сигнал (рис. 1.10, в).

Понятие о геометрических методах создания государственных геодезических сетей.

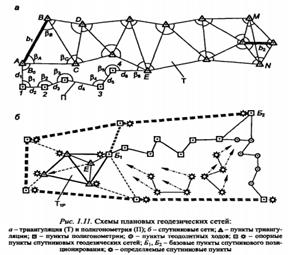
Метод триангуляции состоит в том, что в вершинах всех треугольных фигур, образованных пунктами сети, измеряют горизонтальные углы, а длины сторон, называемых базисными, измеряют только в нескольких треугольниках (базисы Ь\ к bi - рис. 1.11, а). Длины остальных сторон вычисляют по тригонометрическим формулам, находят дирекционные углы сторон и определяют координаты пунктов.

Трилатерация - метод построения геодезических сетей в виде треугольных фигур, в которых измеряются только их стороны (расстояния между центрами геодезических пунктов), а углы между сторонами вычисляют решением треугольников.

Метод полигонометрии основан на построении геодезической сети, состоящей из ломаных линий, называемых ходами, вершины которых закреплены геодезическими пунктами (см. рис. 1.11, а).

Пункты государственных геодезических сетей 1-го и 2-го классов являются исходными для развития геодезических сетей любого назначения на территории государства. Расстояния между ними составляют 7-25 км. Для увеличения плотности исходных геодезических пунктов внутри сетей 1-го и 2-го классов выполняется развитие сетей триангуляции и полигонометрии 3-го и 4-го классов (длины сторон 2-8 км).

Государственные нивелирные сети 1, 2, 3 и 4-го классов на местности закреплены постоянными знаками - реперами (рис. 1.12), которые закладывают или в грунт (грунтовые реперы), или в стены капитальных зданий и сооружений (стенные реперы). Высотная координата (отметка) репера в прошлом определялась только наземными способами нивелирования (измерения превышений), которые по точности подразделяются на нивелирование I, П, III и IV классов. Погрешности нивелирования в прямом и обратном направлениях, т.е. нивелирования двойным ходом, соответственно характеризуются величинами 0,5; 2; 4 и 8 мм на 1 км нивелирного хода.

Плановые сети сгущения.

Сети сгущения необходимы

для увеличения количества опорных пунктов на территории строительства или крупного промышленного предприятия при геодезическом обеспечении съемочных, строительных или горных работ. Сети сгущения создаются относительно пунктов более высокого класса точности методами триангуляции или полигонометрии (см. рис. 1.11, б). Дополнительные пункты сетей сгущения (например, пункт Е) определяются различными способами: триангуляционным, прямой или обратной угловыми засечками и др.

По точности эти сети подразделяются на сети 1-го и 2-го разрядов. Они опираются на геодезические пункты более высокого класса точности. Средние квадратические погрешности измерения углов в разрядных сетях составляют 5" и 10", относительные погрешности сторон в слабом месте не более 1/20 ООО и 1/10 ООО.

13. Съемочное плановое и высотное обоснование, его назначение, схема построения.}

Съемочное геодезическое обоснование предназначено для координатной привязки в плане и по высоте материалов топографических съемок, изыскательских, инженерно-геодезических и других работ. Съемочное обоснование развивается внутри сетей сгущения. Места для пунктов съемочного обоснования выбирают с учетом технологии предстоящих съемочных и изыскатель­

ских работ и закрепляют постоянными или временными знаками (деревянными кольями или металлическими стержнями).Координаты пунктов съемочного обоснования определяют

полишнометрией (см. рис. 1.11, б), микротриангуляцией и различными засечками технической точности, при этом углы в треугольных фигурах не должны быть меньше 30° и больше

150°, а длина их сторон не больше 150-250 м. Полигонометрический ход технической точности называют теодолитным ходом, в нем углы измеряются со средней квадратической по­

грешностью 0,5', стороны длиной от 20 до 350 м - с допустимой относительной погрешностью 1/1000-1/3000.

Сети специального назначения создаются для геодезического обеспечения строительства, как правило, уникальных энергетических, гидротехнических, мелиоративных и других сооружений. Методы создания таких сетей могут быть любыми из рассмотренных, но при этом точность определения взаимного положения пунктов может существенно превосходить любые из

ранее рассмотренных. Этого добиваются применением специальных методик и приборов для производства измерений. Для закрепления координированных точек используют специальные

типы центров, обеспечивающие их стабильное пространственное положение на период строительства и эксплуатации объекта.Каталоги координат и высот геодезических пунктов.

Плановые и высотные координаты пунктов геодезической сети приводятся в отдельных каталогах координат или высот пунктов, которые хранятся в организациях, ведущих геодези­

ческие работы, и в районных, областных и республиканских органах геодезического надзора Государственного комитета по имуществу Республики Беларусь.

14. Закрепление геодезических сетей плановыми и высотными пунктами,схемы построения}Государственные нивелирные сети 1, 2, 3 и 4-го классов на местности закреплены постоянными знаками - реперами (рис. 1.12), которые акладывают или в грунт (грунтовые реперы), или в стены капитальных зданий и сооружений (стенные реперы). Высотная координата (отметка) репера в прошлом определялась только наземными способами нивелирования (измерения превышений), которые по точности подразделяются на нивелирование I, П, III и IV классов. Погрешности нивелирования в прямом и обратном направлениях, т.е. нивелирования двойным ходом, соответственно характеризуются величинами 0,5; 2; 4 и 8 мм на 1 км нивелирного хода, допустимые невязки превышений определяются соответственно классу нивелирования следующими величинами 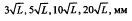где L - длина хода, км.

15.Методы построения геодезич. сетей(триангуляция,трилатерация,полигонометрия)

Понятие о геометрических методах создания государственных геодезических сетей. Метод триангуляции состоит в том, что в вершинах всех реугольных фигур, образованных пунктами сети, измеряют горизонтальные углы, а длины сторон, называемых базисными, измеряют только в нескольких треугольниках (базисы Ь₁ к b₂ - рис. 1.11, а). Длины остальных сторон вычисляют по тригонометрическим формулам, находят дирекционные углы сторон и определяют координаты пунктов. Трилатерация - метод построения геодезических сетей в виде треугольных фигур, в которых измеряются только их стороны (расстояния между центрами геодезических пунктов), а углы между сторонами вычисляют решением треугольников. Метод полигонометрии основан на построении геодезической сети, состоящей из ломаных линий, называемых ходами, вершины которых закреплены геодезическими пунктами (см. рис. 1.11, а). Измеряются длины d сторон хода и горизонтальные углы 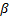между ними. Полигонометрические ходы опи­

раются на пункты триангуляции, относительно которых вычисляются плановые координаты пунктов хода, а их высотные координаты определяются нивелированием.Пункты государственных геодезических сетей 1-го и2-го классов являются исходными для развития геодезических сетей любого назначения на территории государства. Расстояния между ними составляют 7-25 км. Для увеличения плотности исходных геодезических пунктов внутри сетей 1-го и 2-го классов выполняется развитие сетей триангуляции и полигонометрии 3-го и 4-го классов (длины сторон 2-8 км). Погрешности расстояний между соседними пунктами составили 5 - 15 см (в относительной мере от 1 : 300 ООО до 1 : 25 ООО).Точность измерения углов триангуляции 1 ,2 ,3 и 4-го классов характеризуется средними квадратическими погрешностями 0,7"; 1"; 1,5" и 2", а средние квадратические относительные погрешности определения длины сторон в слабом месте (вдали от базисов) - относительными погрешностями 1/200 ООО;

1/150 ООО; 1/120 ООО; 1/25 ООО.В государственных полигонометрических сетях 1, 2, 3 и 4-го классов горизонтальные углы измерялись со средними квадратическими погрешностями 0,4"; 1"; 1,5" и 2", длина сторон - с относительными средними квадратическими погрешностями 1/300 ООО; 1/250 000;

16. Топографические карты и планы, различие между ними, масштабы планов и карт.

Обширные территории изображают на картах в определен­

ном масштабе. Под масштабом карты подразумевают отно­

шение длины отрезка на карте к длине соответствующего от­

резка на местности. Масштаб карты выражается в виде обык­

новенной дроби, числитель которой равен единице. Например,

масштаб, равный 1 : 100000, указывает на то, что отрезок на

местности изображается на карте в среднем уменьшенным в

100000раз, или 1 см на карте соответствует 1 км на местно­

сти. Контуры и точки земной поверхности, отнесенные к по­

верхности земного эллипсоида или шара, проецируют на кар­

тинную плоскость, а с нее на карту по определенным математи­

ческим законам, используя методы генерализации и обобщения.

Высоты точек и рельеф местности на картах отображаются в

Балтийской системе высот.

Топографические карты создают в конформной проекции

эллипсоида на плоскость в масштабах 1 : 1 000000 и более крупных - 1 : 100 000

Топографический план представляет собой уменьшенное и подобное

изображение контуров и рельефа участка местности в ортогональной проекции на горизонтальную плоскость.

К картографическим материалам относят также и профили - уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного направления.

При составлении профиля земной поверхности и сооружений линейного вида для чертежа обычно берут масштаб вертикальных расстояний 1 : в 10 раз крупнее масштаба горизонтального 1 : 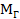. На профилях проектируют надземные и подземные линейные объекты (дороги, трубопроводы, каналы, тоннели и т.д.) и отображают вертикальные разрезы построенных сооружений.

Масштабы топографических и маркшейдерских чертежей, профилей представляют в численном виде и в графической форме.

Численный масштаб 1 : М – это отношение длины отрезка 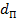на плане к горизонтальному проложению соответствующего отрезка на местности: 1 : М =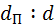

Знаменатель М численного масштаба характеризует величину уменьшения горизонтальных проложений при их изображении на плане: М =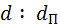

Если 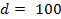м, 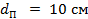, то М 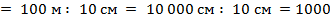, т. е. численный масштаб

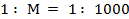(одна тысячная). Численный масштаб часто указывается в словесной форме, например “в 1 см 10 м” – для плана масштаба 1 : 1000.

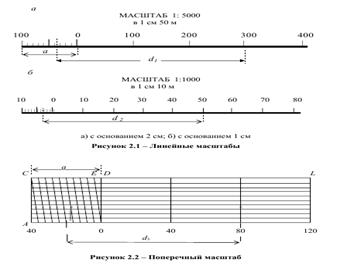
Линейный масштаб представляет собой отрезок прямой, на котором несколько раз отложен отрезок а, называемый основанием масштаба. На рис. 2.1, 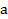основание аравно 2 см, левый отрезок крайний отрезок разделен наименьшими делениями на 10 равных частей. Для плана масштаба 1 : 5000 (в 1 см 50 м) основанию, равному 2 см, соответствует расстояние на местности 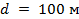, поэтому деления а подписаны через 100 м.

Поперечный масштаб предназначен для более точных измерений по плану. Точность масштаба. Понятие точности масштаба соответствует способности человека с расстояния 25–30 см различать невооруженным глазом на плане точку диаметром около 0,1 мм. Точностью масштаба t называют горизонтальный отрезок 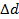на местности, соответствующий отрезку длиной 0,1 мм на плане масштаба 1 / М: t=0.0001м

Например, точность масштаба 1:500 (в 1 см 5 м) будет равна

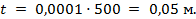
Погрешности расстояний, измеренных по плану (карте). По ряду причин (погрешности съемочных работ, составления планов, печатания копий топографического чертежа, деформаций бумажной основы) изображения объектов местности на карте или на рабочем плане находятся каждое не на своем месте, а со средним отклонением от него 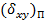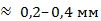(в отдельных случаях отклонения достигают 0,7–1 мм). Расстояние 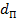, измеряемое между такими точками по плану масштаба 1:М, получается со средней вероятной погрешностью 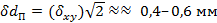. Средняя погрешность расстояния, измеренного по карте, оценивается по формуле .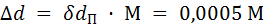