Обучение многослойной сети с помощью с помощью алгоритма обратного распространения.

Является обобщением процедуры обучения простого перцептронас использованием дельта-правила на многослойные сети. В данном методе необходимо располагать обучающей выборкой, содержащей «правильные ответы», т.е. выборка должна включать множество пар образцов входных и выходных данных, между которыми нужно установить соответствие. Перед началом обучения межнейронным связям присваиваются небольшие случайные значения. Каждый шаг обучающей процедуры состоит из двух фаз. Во время первой фазы входные элементы сети устанавливаются в заданное состояние. Входные сигналы распространяются по сети, порождая некоторый выходной вектор. Для работы алгоритма требуется, чтобы характеристика вход-выход нейроподобных элементов была неубывающей и имела ограниченную производную. Обычно для этого используют сигмоидальные функции. Полученный выходной вектор сравнивается с требуемым (правильным). Если они совпадают, то весовые коэффициенты связей не изменяются. В противном случае вычисляется разница между фактическими и требуемыми выходными значениями, которая передается последовательно от выходного слоя к входному. На основе этой информации проводится модификация связей в соответствии с обобщенным дельта-правилом, которое имеет вид: 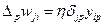, где изменение в силе связи wji для р-й обучающей пары 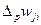пропорционально произведению сигнала ошибки j-го нейрона 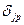, получающего входной сигнал по этой связи, и выходного сигнала i-го нейрона yip, посылающего сигнал по этой связи. Определение сигнала ошибки является рекурсивным процессом, который начинается с выходных блоков. Для выходного блока сигнал ошибки 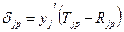, где Tjp и Rjp — соответственно желаемое и действительное значения выходного сигнала j-го блока; 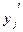- — производная от выходного сигнала j-го блока. Сигнал ошибки для скрытого блока определяется рекурсивно через сигнал ошибки блоков, с которым соединен его выход, и веса этих связей равны 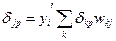. Для сигмоидальной функции 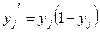, поэтому на интервале 0<yj<1 производная имеет максимальное значение в точке уj=0.5, а в точках уj=0 и уj=1 обращается в ноль. Максимальные изменения весов соответствуют блокам, которые еще не выбрали свое состояние. При конечных значениях весовых коэффициентов выходные сигналы блоков не могут достигать 0 или 1.

Модификация весов производится после предъявления каждой пары вход-выход. Если коэффициент 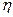, определяющий скорость обучения, мал, то можно показать, что обобщенное дельта-правило достаточно хорошо аппроксимирует минимизацию общей ошибки функционирования сети D методом градиентного спуска в пространстве весов. Общая ошибка функционирования сети определяется по формуле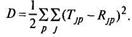

Обучение продолжается до тех пор, пока ошибка не уменьшится до заданной величины. Недостаток: во многих случаях для сходимости может потребоваться многократное предъявление всей обучающей выборки. Повышения скорости обучения можно добиться, используя информацию о второй производной D или путем увеличения 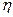. Алгоритм используется также для обучения сетей с обратными связями. При этом используется эквивалентность многослойной сети с прямыми связями и синхронной сети с обратными связями на ограниченном интервале времени.

7. Использование нейронной сети в качестве ассоциативной памяти. Сети Хопфилда и Хэмминга.

Модель Хопфилда. Ему удалось привлечь к анализу нейросетевых моделей мощный математический аппарат статистической физики. В результате была сформулирована математическая модель ассоциативной памяти на нейронной сети с использованием правила Хебба для модификации весовых коэффициентов. Правило основано на предположении: если два нейрона возбуждаются вместе, то сила связи между ними возрастает; если они возбуждаются порознь, то сила связи между ними уменьшается. Сеть Хопфилда строится с учетом условий: все элементы связаны со всеми; wji=wij - прямые и обратные связи симметричны; wii=0 - диагональные элементы матрицы связей равны нулю, т.е. исключаются обратные связи с выхода на вход одного нейрона.

Для однослойной нейронной сети со связями типа «все ко всем» характерна сходимость к одной из конечного множества равновесных точек, которые являются локальными минимумами функции энергии, отражающей структуру всех связей в сети. Введенная Хопфилдом функция вычислительной энергии нейронной сети описывает поведение сети через стремление к минимуму энергии, который соответствует заданному набору образов. Сети Хопфилда могут выполнять функции ассоциативной памяти, обеспечивая сходимость к тому образу, в область притяжения которого попадает начальный образец активности нейронов сети.

Этот подход привлекателен тем, что нейронная сеть для конкретной задачи может быть запрограммирована без обучающих итераций. Веса связей вычисляются на основе вида функции энергии, сконструированной для решаемой задачи.

Развитием модели Хопфилда является машина Больцмана для решения комбинаторных оптимизационных задач и задач искусственного интеллекта. В ней нейрон имеет состояния (1,0), межнейронные связи представлены весовыми коэффициентами, а каждое состояние сети характеризуется определенным значением функции консенсуса. Максимум функции консенсуса соответствует оптимальному решению задачи.

Сети Хопфилда получили применение на практике в основном как реализации подсистем более сложных систем. Недостатки: предположение о симметрии связей между элементами, без которой нельзя ввести понятие энергии; нейронная сеть — устройство для запоминания и обработки информации, а не устройство минимизации энергии. Экономия энергии играет в этих процессах вспомогательную роль; сети Хопфилда поддерживают множество лишних, неэффективных, иногда дублирующих друг друга связей.

Сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений. Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.