Описание экспериментальной установки. Лабораторная установка состоит из осциллографа и стенда

Лабораторная установка состоит из осциллографа и стенда, содержащего две катушки индуктивности, два конденсатора, магазин сопротивлений и генератор импульсов.

Генератор вырабатывает короткие положительные импульсы, в результате чего конденсатор колебательного контура периодически получает некоторый электрический заряд. В промежутках времени между импульсами в контуре будут совершаться затухающие колебания. Графики этих колебаний можно наблюдать на экране осциллографа и определить по ним период, логарифмический декремент затухания, добротность, критическое сопротивление.

Необходимые для расчетов параметры элементов контура указаны на стенде.

Порядок выполнения работы

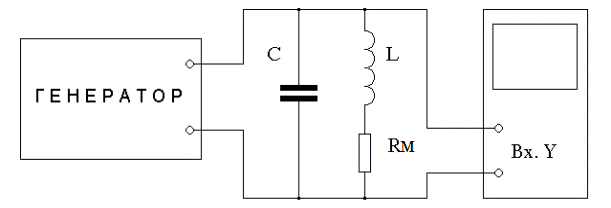1. Собрать схему согласно рис. 11.5. Сопротивление магазина R_м сделать равным нулю. Индуктивность и емкость контура выбрать произвольно, внести их параметры в табл. 11.1.

Рис. 11.5.

2. Включить осциллограф, прогреть его в течение 1-2 минут. Ручкой “Фокус” хорошо сфокусировать луч, чтобы уменьшить ошибку измерений.

3. Включить генератор. С помощью ручек управления разверткой осциллографа добиться неподвижной картины колебаний так, чтобы обеспечить достаточно точное измерение временных интервалов и амплитуд колебаний.

4. С помощью полученной осциллограммы, аналогичной рис. 11.3, измерить период колебаний То при минимальном сопротивлении контура, т.е. при R_М = 0, результат внести в табл. 11.1 в миллисекундах.

Таблица 11.1

№	С, мкФ	L, мГн	RL, Ом	Т0, мс	Rкр, Ом	RМ, Ом	R, Ом	Т, мс
……

Для повышения точности можно измерить промежуток времени, соответствующий нескольким периодам колебаний, разделить его на число периодов и, таким образом, определить длительность одного периода.

5. Увеличивая сопротивление магазина R_М, проследить за возрастанием скорости затухания колебаний и определить критическое сопротивление контура, соответствующее переходу от периодических колебаний к апериодическим (т.е. переходу осциллограммы от рис. 11.2,в к рис. 11.2,г):

R_кр = R_L + R _М,

где R_L - собственное сопротивление катушки индуктивности. Полученное значение R_кр внести в табл. 11.1.

6. Уменьшить сопротивление R_М, например, вдвое от R_кр. В контуре вновь возникнут затухающие периодические колебания. Определить период этих колебаний Т и вместе с полученным значением сопротивления контура (R = R_L + R_М) занести в табл. 11.1. Убедиться в различии периодов колебаний Т₀ и Т, соответствующих различным значениям сопротивления контура.

7. Повторить измерения по пунктам 4 - 6 три раза для различных комбинаций L и C .

8. Для выбранных значений емкости C, индуктивности L, сопротивления R_L и полного сопротивления контура R, внесенных в табл. 11.1, вычислить и занести в табл. 11.2 теоретические значения:

T₀ - по формуле (11.10); T - по формуле (11.9);

R_кр - по формуле (11.12); d - по формуле (11.14),

Q - по формуле (11.20).

Таблица 11.2

№	Т0, мс	Т, мс	Rкр, Ом	d	Q
… …

9. Для произвольных значений L и C исследовать зависимость логарифмического декремента затухания от сопротивления контура. Увеличивая сопротивление контура с помощью магазина сопротивлений R, измерить амплитуды А₁ и А₂, которые соответствуют моментам времени, отличающимся на период (рис.11.3).

Результаты измерений внести в табл. 11.3. Подсчитать экспериментальные значения логарифмического декремента затухания d_э по формуле (11.13), по формуле (11.14) - его теоретические значения d_т.

Таблица 11.3

№	R, Ом	А1, мм	А2, мм	dэ	dт

10. Для наблюдения фазовых кривых собрать схему по рис. 11.6.

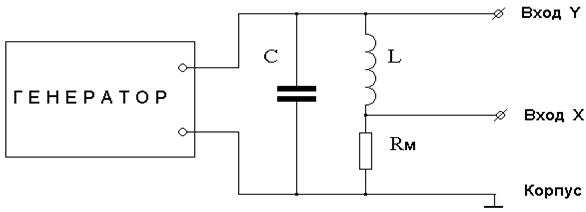
Рис. 11.6.

При этом на вход X подается сигнал с сопротивления Rм, который находится в фазе с током в контуре. На вход Y подается сигнал, находящийся в фазе с напряжением. Наблюдая фазовые кривые для различных сопротивлений контура, можно исследовать влияние затухания на форму фазовой кривой и уточнить значение критического сопротивления для данных значений емкости и индуктивности (рис. 11.4,г).

С помощью фазовых кривых можно провести также измерения по п.9 (рис. 11.4,б).

11. Для одновременного наблюдения осциллограмм колебаний тока и напряжения и определения сдвига фаз между ними собрать схему в соответствии с рис. 11.7.

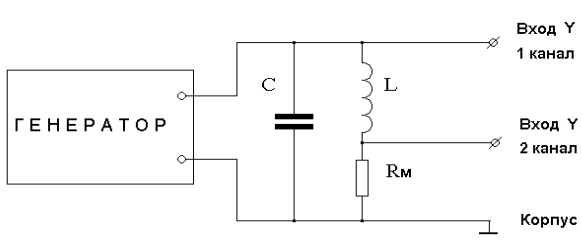
Рис. 11.7.

На входы Y первого и второго каналов осциллографа подаются сигналы, пропорциональные напряжению и току в контуре. Убедиться в наличии сдвига фаз этих колебаний, оценить величину этого сдвига.

Контрольные вопросы

1. Рассказать об электрических колебаниях в контуре.

2. Дать определение амплитуды, частоты, фазы, периода колебаний.

3. Какой процесс называется апериодическим? Что такое критическое сопротивление? Вывести уравнение (11.12).

4. Какие превращения энергии имеют место при периодическом и апериодическом процессах?

5. Какие формулы описывают энергию электрического поля конденсатора и энергию магнитного поля катушки.

6. Вывести уравнение затухающих электрических колебаний.

7. Что такое логарифмический декремент затухания? Объяснить его физический смысл, вывести уравнение (11.15).

8. Пояснить физический смысл добротности контура. Вывести уравнение (11.20).

9. Что называется фазовой кривой? Получить уравнение этой кривой.

10. Вывести уравнение (11.7), применив закон Ома для неоднородной замкнутой цепи.

11. Какова величина сдвига фаз между колебаниями тока и напряжения в идеальном колебательном контуре? Как можно измерить ее в реальных условиях?

12. Рассказать о практическом применении колебательного контура в технике.