Порядок выполнения работы. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-I»

В. И. МАРЧЕНКО

ИЗУЧЕНИЕ ЯВЛЕНИЯ

ВЗАИМНОЙ ИНДУКЦИИ

Методические указания

к лабораторной работе

По дисциплине «Физика»

№244

МОСКВА – 2006

УДК 531

М - 37

Марченко В.И. Изучение явления взаимной индукции. Методические указания к лабораторной работе. – М.: МИИТ, 2006,– 13 с.

Изложена физическая суть явления взаимной индукции. Дано описание экспериментальной установки для его изучения на основе стандартного измерительного модуля ФПЭ-05, состоящего из двух аксиальных подвижных катушек, подключаемых к источнику переменного тока с регулируемыми напряжением и частотой. Соответствует программе дисциплины «Физика» (раздел «Электричество и магнетизм»). Предназначено для студентов 1 и 2 курсов энергетических, механических и строительных специальностей.

Ó Московский государственный университет путей сообщения

( МИИТ), 2006

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-I»

В. И. Марченко

Утверждено

редакционно-издательским

советом университета

ИЗУЧЕНИЕ ЯВЛЕНИЯ

ВЗАИМНОЙ ИНДУКЦИИ

Методические указания к лабораторной работе по дисциплине «Физика» №244 для студентов 1 и 2 курсов энергетических, механических и строительных специальностей.

Москва – 2006

Работа № 244 «Изучение явления взаимной индукции»

Цель работы: экспериментальное изучение явления взаимной индукции двух коаксиально расположенных катушек и измерение величин коэффициентов их взаимной индуктивности при различном расположении и разных значениях частоты и амплитуды переменного тока.

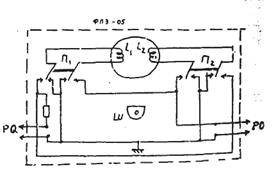
Приборы и принадлежности: измерительный модуль ФПЭ-05 (общий вид модуля приведен на рис.1); генератор переменного тока звуковой частоты (PQ); электронный осциллограф (PO); две аксиальные катушки индуктивности L₁ и L₂, расположенные на одной оси; шток (Ш) с нанесенной на нем шкалой, по которой определяется взаимное расположение катушек.

Рис. 1

Введение.

Явление взаимной индукции является частным случаем открытого М. Фарадеем (1831 г.) явления электромагнитной индукции, заключающегося в наведении электродвижущей силы в контуре при изменении потока вектора индукции магнитного поля B через площадь, ограниченную этим контуром. Наблюдать явление взаимной индукции можно с помощью двух контуров 1 и 2, отстоящих друг от друга на некотором расстоянии (рис. 2).

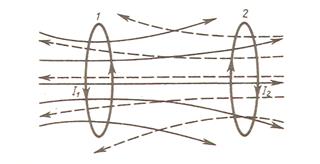
Рис. 2

Когда по одному из контуров (например, по контуру 1) протекает электрический ток I₁, то в пространстве, окружающем этот ток, возбуждается магнитное поле. Индукция магнитного поля B в тех точках, где расположен контур 2, зависит от силы тока I₁ и расстояния между контурами 1 и 2. Если линии индукции магнитного поля тока I₁ пересекают площадь, ограниченную контуром 2, то такие контуры называются магнитосцепленными. Поток вектора B через поверхность магнитосцепленного контура 2 Φ_2,1 = ∫B_ndS зависит от силы тока I₁, протекающего в

^S

контуре 1, и от площади и расположения контура 2 (под расположением контура 2 подразумевается не только расстояние между контурами 1 и 2, но и их пространственная ориентация). Теория и опыт показывают, что в неферромагнитных средах:

Φ_2,1 = L_2,1∙ I₁ (1)

Коэффициент пропорциональности в равенстве (1) L_2,1 называется коэффициентом взаимной индуктивности контуров. Он показывает, какой поток (выраженный в веберах) пронизывает данный контур при протекании в другом, магнитосцепленным с ним, контуре тока силой в 1 А. За единицу измерения коэффициента взаимной индуктивности в СИ принят генри (Гн). Взаимной индуктивностью в 1 Гн обладают такие два магнитосцепленных контура, которые отвечают следующему требованию: при протекании в одном контуре постоянного тока силой 1 А, поток вектора индукции возбужденного им магнитного поля через площадь, ограниченную вторым контуром, равен 1 Вб (1 Вб = 1 Тл∙м²).

Все приведенные выше рассуждения можно повторить для случая, когда в контуре 2 протекает ток I₂, и показать, что поток вектора индукции магнитного поля тока I₂ через площадь, ограниченную контуром 1, будет выражаться такой же зависимостью:

Φ_1,2 = L_1,2∙ I₂ (1`)

Согласно теореме взаимности рассматриваемого явления и предположения, что контуры размещены в неферромагнитной среде с постоянной, не зависящей от силы тока магнитной проницаемостью μ≈1, следует, что:

L_2,1 = L_1,2

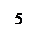По закону Фарадея для электромагнитной индукции электродвижущая сила, которая наводится в контуре, прямо пропорциональна скорости изменения потока вектора индукции магнитного поля (в дальнейшем магнитного потока) через площадь поверхности, ограниченной контуром:

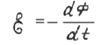
(2)

(знак “-“ соответствует правилу, установленному Х. Ленцом для этого явления).

Одним из способов изменения магнитного потока Φ через площадь поверхности, ограниченной каким-либо из контуров, согласно (1) и (1`), является изменение силы тока в другом, магнитосцепленном с ним контуре. И тогда, если в контуре 1 произойдет изменение силы тока, то в контуре 2 будет наводиться электродвижущая сила, которая, согласно закону Фарадея (2), будет зависеть от скорости изменения тока I₁:

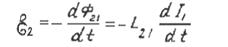
(3)

Точно так же при изменении силы тока I₂ в контуре 2 в контуре 1 будет наводиться электродвижущая сила:

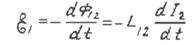(4)

Таким образом, явление взаимной индукции – это явление наведения электродвижущей силы (в дальнейшем ЭДС) в контуре при изменении силы тока в другом, магнитосцепленном с ним, контуре.

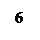
Метод измерений.

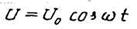В данной работе изучается явление взаимной индукции можду длинной катушкой I и короткой катушкой 2, которая надевается на катушку I и может перемещаться вдоль ее оси. Одна из кату­шек, например I, включается в цепь генератора переменного тока звуковой частоты (PQ), напряжение, на выходе которого изменяется по закону:

(5)

Вольтметром, расположенным на пане­ли генератора PQ, измеряются действующие значения напряжения U_d = U_o/Ö2. Последовательно с катушкой подключено сопротивление R, выбранное таким образом, чтобы выполнялось неравенство:

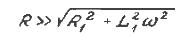(6)

(где L₁ - индуктивность катушки I; R₁ - ее активное сопротивление, w - циклическая частота переменного напряжения). В этом случае сдвиг по фазе между током и напряжением, обусловленный индуктивным сопротивлением катушки, равным L₁w, становится малым, и ток, протекающий через катушку I, можно опреде­лить по закону Ома:

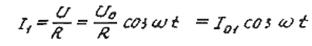(7)

(где I_0,1 - амплитудное значение силы переменного тока).

Переменный ток в катушке I возбуждает переменную ЭДС взаимной ин­дукции в катушке 2:

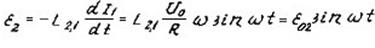
(8)

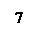(где e_0,2 - амплитудное значение переменной ЭДС взаимной индукции).

Как видно из (8), амплитуда ЭДС взаимной индукции

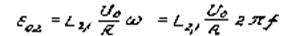
(9)

(где f - частота переменного напряжения на выходе звукового генератора в Гц, связанная с циклической частотой соотношением w = 2pf).

Из (9) имеем:

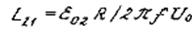
(10)

Если поменять местами катушки I и 2, то можно таким же образом найти:

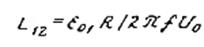
(11)

Катушки 1 и 2 не имеют ферромагнитных сердечников или иных деталей, способных сильно намагничиваться, и поэтому, как и в случае с рассмотренным выше примером контуров 1 и 2, L_2,1=L_1,2.

Для измерения амплитудных значений ЭДС взаимной индукции e_0,1 иe_0,2 используется осциллограф PO. Процедура измерения приведена в отдельной инструкции, размещенной на панели модуля ФПЭ-05.

Рис. 3

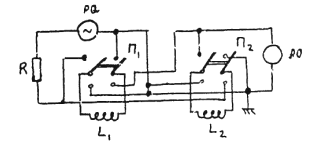
Для перемены местами катушек I и 2 необходимо перебросить переключатели П₁ и П₂ в противоположное положение (рис. 3).

Порядок выполнения работы.

Задание I. Измерение коэффициентов взаимной индуктивности L_2,1 и L_1,2 и исследование их зависимости от взаимного расположения катушек.

1. Соберите схему, изображенную на рис. 4 и 5.

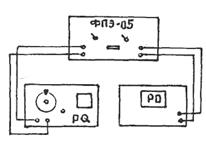
Рис. 4 Рис. 5

2. Ознакомьтесь с инструкцией по работе с электронным осциллографом и звуко­вым генератором.

3. Установите напряжение U_д и частоту f переменного напряжения на выходе генератора PQ (по указанию преподавателя) и подайте его на катушку I (с помощью преключателя П₁).

4. С помощью переключателя П₂ подайте ЭДС, индуцируемую в катушке 2, на осциллограф PO.

5. Установите подвижную катушку I в крайнее положение. Переме­щая ее в противоположное крайнее положение через 1 см, записывайте значения ЭДС взаимной индукции в цепи катушки 2 в таблицу 1.

Таблица 1

Uд = . . . В f = . . . Гц
r, см	e0,2	L2,1, Гн	e0,1	L1,2,   Гн
дел.	В	дел.	В
1. 2. 3. 4. . . . 10.

6. По формуле (10) рассчитайте значенияL_2,1. Полученные данные занесите в таблицу 1.

7. Поменяв местами катушки L₁ и L₂(с помощью переключателей П₁и П₂), повторите измерения по пп. 2, 3 и рассчитайте L_1,2.

Задание 2. Измерение коэффициента взаимной индуктивности L_2,1 при различных значениях амплитуды переменного напряжения.

1. Поставьте катушку I в среднее положение относительно катушки 2.

2. Задайте частоту на выходе генератора PQ по указанию преподавателя (например, 10⁴ Гц).

3. Измерьте амплитуду ЭДС взаимной индукции e_0,2 при различных значениях напряжения U_д вцепи катушки I в интервале 0 – 5, через 1 В.

4. По формуле (10) рассчитайте L_2,1. Полученные данные занесите в таблицу 2.

Таблица 2

R = 104 Ом f = . . . Гц
Uд, В
e0,2, В
L2,1, Гн

Задание 3. Измерение коэффициента взаимной индуктивности L_2,1 при различных частотах переменного напряжения.

1. Поставьте катушку I в среднее положение относительно катушки 2.

2. Установите амплитуду напряжения на выходе генератора PQ по указанию преподавателя (например, 2 В).

3. Измерьте амплитуду ЭДС взаимной индукции e_0,2 при различных частотах переменного напряжения от 5 до 20 кГц (не менее 5 значений).

4. По формуле (10) рассчитайте L_2,1. Полученные данные занесите в таблицу 3.

Таблица 3

R = 104 Ом Uд = . . . В
f, Гц
e0,2, В
L2,1, Гн