Задачи, рекомендуемые для занятий
1. Определите среднюю плотность некоторой планеты, если продолжительность суток на ней составляет б ч, а пружинные весы на экваторе показывают на 10 % меньший вес, чем на полюсе.
2. Масса некоторой планеты в 2 раза больше Земли, а радиус равен радиусу Земли. Определите ускорения свободного падения на поверхности этой планеты.
3. Два спутника движутся вокруг Земли по круговым орбитам, лежащим в одной плоскости, со скоростями 7,8 км/с и 7,6 км/с. Определите минимальное расстояние между спутниками и промежуток времени, через который они вновь будут находиться на таком же расстоянии.
4. Космическая ракета летит на Луну. В какой точке прямой, соединяющей центры земли и Луны ракета будет притягиваться к Земле и Луне с одинаковой силой?
5. Сравнить ускорение силы тяжести на поверхности Луны с ускорением силы тяжести на поверхности Земли.
6. Найти линейную скорость движения Луны по орбите. Орбиту Земли считать круговой.
7. Найти изменение ускорения силы тяжести при на Земле при опускании тела на глубину h. На какой глубине ускорение силы тяжести составляет 25% от ускорения силы тяжести на поверхности Земли? Плотность Земли считать постоянной, и не учитывать притяжение верхних слоев Земли.
8. Найти численное значение первой и второй космической скорости для Луны.
9. На каком расстоянии от поверхности Земли ускорение силы тяжести равно 1 м/с2.
10. Планета Марс имеет два спутника – Фобос и Деймос. Первый находится на расстоянии 9500 км от центра Марса, второй на расстоянии 24000 км. Найти периоды обращения спутников вокруг Марса.
Занятие 6 .Статика и гидродинамика жидкостей и газов.
1. Давление. Распределение давления в покоящихся жидкости и газе.
2. Выталкивающая сила.
3. Линии и трубки тока. Неразрывность струи. Закон Бернулли.
4. Измерение давления в текущей жидкости. Применение закона сохранения энергии к движению жидкости.
5. Силы внутреннего трения. Ламинарное и турбулентное течение.
6. Движение тел в жидкостях и газах.
Для установившегося движения идеальной несжимаемой жидкости справедлив закон Бернулли:
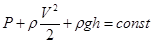 , где
, где 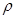 - плотность жидкости,
- плотность жидкости, 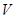 – скорость течения жидкости,
– скорость течения жидкости, 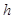 –высота данного сечения трубы над некотором уровнем,
–высота данного сечения трубы над некотором уровнем, 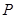 – давление.
– давление.
Скорость вытекающей струи из малого отверстия равна 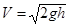 .
.
Так как через любое поперечное сечение трубы проходят равные объемы жидкости, то 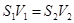 .
.
Сила сопротивления, которую испытывает падающий в вязкой жидкости (или в газе) шарик определяется формулой Стокса 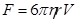 , где
, где 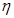 - коэффициент внутреннего трения жидкости или газа (динамическая вязкость),
- коэффициент внутреннего трения жидкости или газа (динамическая вязкость), 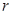 - радиус шарика,
- радиус шарика, 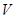 - скорость шарика.
- скорость шарика.
Закон Стокса справедливы только для ламинарного движения. При ламинарном движении жидкости объем жидкости или газа протекающей за время 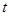 капиллярную трубку радиусом
капиллярную трубку радиусом 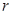 и длиною
и длиною 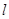 , определяется формулой Пуазейля
, определяется формулой Пуазейля 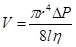 , где
, где 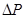 – разность давлений на концах трубки.
– разность давлений на концах трубки.
Характер движения жидкости и газа определяется безразмерным числом Рейнольдса 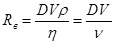 , где
, где 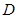 – величина, характеризующая линейные размеры тела,
– величина, характеризующая линейные размеры тела, 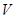 – скорость течения,
– скорость течения, 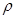 - плотность,
- плотность, 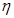 - динамическая вязкость. Отношение
- динамическая вязкость. Отношение 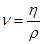 называется кинематической вязкостью. Критическое значение числа Рейнольдса, определяющее переход от ламинарного течения к турбулентному зависит от формы тела.
называется кинематической вязкостью. Критическое значение числа Рейнольдса, определяющее переход от ламинарного течения к турбулентному зависит от формы тела.
