Вынужденные гармонические колебания пружинного маятника

Незатухающие гармонические колебания в реальной колебательной системе можно получить с помощью внешней вынуждающей силы F(t), изменяющейся по гармоническому закону: .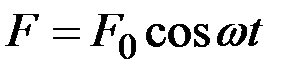

Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями.

Второй закон Ньютона для вынужденных колебаний пружинного маятника:

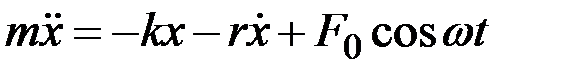
или

.

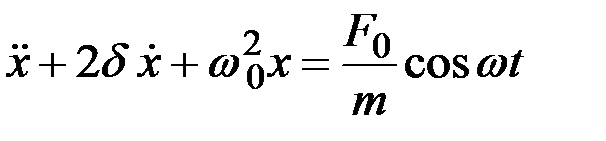Полученное выражение представляет собой дифференциальное уравнение вынужденных гармонических колебаний пружинного маятника.

Решением этого дифференциального уравнения является функция :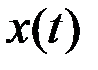

.

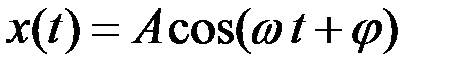При этом амплитуда вынужденных колебаний определяется по формуле:

.

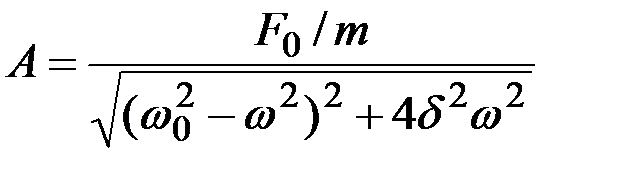Из этой формулы следует, что амплитуда колебаний А имеет максимум при частоте , называемой резонансной частотой :

.

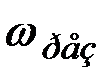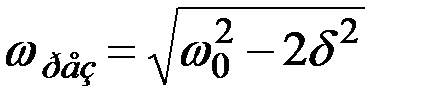Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом.

Тема 8. Гармонические колебания физического маятника

Физический маятник – это твердое тело, имеющее ось вращения и совершающее колебания под действием тангенциальной составляющей силы тяжести F_t (F_t = mgsina (рис. 7), где a – отклонение физического маятника от положения равновесия).

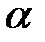l

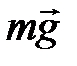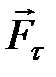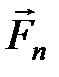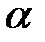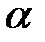Рис. 7

Если физический маятник массой m отклонен от положения равновесия на некоторый угол a , то момент M возвращающей силы F_t :

,

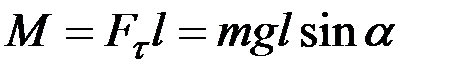где l – плечо силы F_t , то естьрасстояние от центра масс (точка С) до оси маятника (рис. 7).

В случае малых колебаний физического маятника,то есть для малых углов отклонения маятника от положения равновесия sina » a и тогда

.

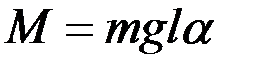По второму закону Ньютона для вращательного движения твердого тела:

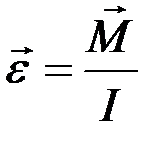или ,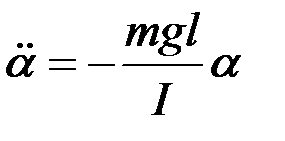

где I — момент инерции маятника относительно его оси.

Знак минус в последнем уравнении обусловлен тем, что вектора момента возвращающей силы 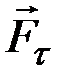и угла поворота 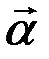имеют противоположные направления.

Обозначив 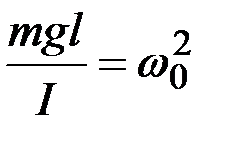, получим дифференциальное уравнение свободных незатухающих гармонических колебаний физического маятника:

.

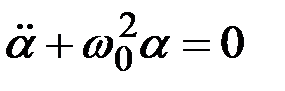Решением этого дифференциального уравнения является функция :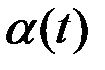

,

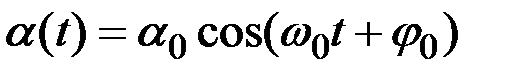где 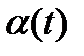– отклонение физического маятника от положения равновесия в момент времени t;

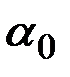– амплитудаколебаний;

w₀ – круговая (циклическая) частота;

(w₀t+j₀) – фаза колебаний в момент времени t;

j₀ –начальная фаза колебаний.

Период малых гармонических колебаний физического маятника:

.
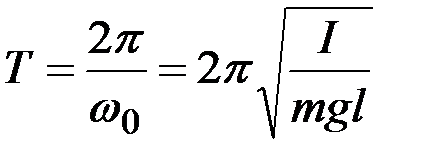