Закон постоянства двухгравных углов

Кристаллы одного и того же вещества могут иметь весьма разнообразную форму. Форма кристалла, как указывалось выше, зависит от условий кристаллизации. Цвет также не является характерным признаком кристаллов данного вещества, так как он очень сильно зависит от примесей. Известно, например, что кристаллы плавикового шпата могут быть бесцветными, розовыми, чёрными, фиолетовыми, тёмно-вишнёвыми и золотистыми. Казалось бы, что установление принадлежности двух кристаллов (отличающихся друг от друга и формой и цветом) одному веществу нельзя произвести иначе, как определив их химический состав. Однако кристаллографы установили на первый взгляд в высшей степени поразительный факт: в кристаллах одного вещества углы между соответственными гранями всегда одинаковы (закон постоянства углов).

Что понимают под соответственными гранями?

В геометрии грани (плоские многоугольники) считаются равными, если они при наложении совпадают всеми своими точками. В кристаллографии равенство граней означает совершенно иное. Грани могут отличаться между собой по форме и всё-таки считаться равными, если они обладают одинаковыми физическими и химическими свойствами. Установить равенство граней в кристаллографическом смысле удаётся иногда путём внешнего их осмотра.

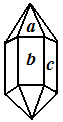
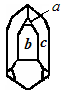Рис2

Рис.1

В сомнительных случаях производят травление поверхности кристалла кислотой. На равных гранях рисунок, полученный при травлении, бывает одинаковым.

На рисунке 1 одинаковой штриховкой показаны одинаковые (равные) грани. В кристалле кварца можно установить три сорта граней (на рис.2 они отмечены буквами a,b и c). Хотя в разных кристаллах кварца грани a (b,c) имеют разный размер и форму, они считаются равными.(В современных школьных учебниках геометрии такие фигуры называют конгруэнтными.)

Закон постоянства углов утверждает, что двугранный угол, образованный гранями a и b (рис.2) в различных кристаллах данного вещества, будет один и тот же. Соответственно во всех кристаллах данного вещества будут равны между собой и двугранные углы, образованные гранями a и c, b и c.

Итак, не форма кристаллов, не размер граней, а угол между ними является определенной величиной для каждого кристалла.

Для измерения углов между гранями применяют специальный прибор – гониометр. . Измерив углы между гранями неизвестного кристалла, можно по специальному каталогу определить химический состав кристалла.

Элементы симметрии

Симметрия» в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.

По более точному определению симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости). Подавляющее большинство кристаллов обладает симметрией.

Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии, ось симметрии, центр симметрии, или центр инверсии.

Плоскость симметрии делит кристалл на две зеркально равные части. Обозначается она буквой Р. Части, на которые плоскость симметрии рассекает многогранник, относятся одна к другой, как предмет к своему изображению в зеркале разные кристаллы имеют различное количество плоскостей симметрии, которое ставится перед буквой Р. Наибольшее количество таких плоскостей у природных кристаллов – девять 9Р. В кристалле серы насчитывается 3Р, а у гипса только одна. Значит, в одном кристалле может быть несколько плоскостей симметрии. В некоторых кристаллах плоскость симметрии отсутствует.

Относительно элементов ограничения плоскость симметрии может занимать следующее положение:

1. проходит через ребра;

2. лежать перпендикулярно к ребрам в их серединах;

3. проходить через грань перпендикулярно к ней;

4. пересекать гранные углы в их вершинах.

В кристаллах возможны следующие количества плоскостей симметрии: 9Р, 7Р, 6Р, 5Р, 4Р, 3Р, 2Р, Р, отсутствие плоскости симметрии.

Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол фигура совмещается сама с собой в пространстве. Она обозначается буквой L. У кристаллов при вращении вокруг оси симметрии на полный оборот одинаковые элементы ограничения (грани, ребра, углы) могут повторяться только 2, 3, 4, 6 раз. Соответственно этому оси будут называться осями симметрии второго, третьего, четвертого и шестого порядка и обозначаться: L2, L3, L4 и L6.Порядок оси определяется числом совмещений при повороте на 360⁰С.

Ось симметрии первого порядка не принимается во внимание, так как ею обладают вообще не фигуры, в том числе и несимметричные. Количество осей одного и того же порядка пишут перед буквой L: 6L6, 3L4 и т.п.

Центр симметрии – это точка внутри кристалла, в которой пересекаются и делятся пополам линии, соединяющие одинаковые элементы ограничения кристалла (грани, ребра, углы). Обозначается она буквой С. Практически присутствие центра симметрии будет сказываться в том, что каждое ребро многогранника имеет параллельное себе ребро, каждая грань – такую же параллельную себе зеркально-обратную грань. Если же в многограннике присутствуют грани, не имеющие себе параллельных, то такой многогранник не обладает центром симметрии.

Достаточно поставить многогранник гранью на стол, чтобы заметить, имеется ли сверху такая же параллельная ей зеркально-обратная грань. Конечно, на параллельность нужно проверить все типы граней.

Существует ряд простых закономерностей, по которым сочетаются друг с другом элементы симметрии. Значение этих правил облегчает их нахождение.

1.Линия пересечения двух или нескольких плоскостей является осью симметрии. Порядок такой оси равен числу пересекающихся в ней плоскостей.

2.L6 может присутствовать в кристалле только в единственном числе.

3.С L6 не могут комбинироваться ни L4, ни L3, но может сочетаться L2 причем L6 и L2 должны быть перпендикулярны; в таком случае присутствует 6L2.

4.L4 может встречаться в единственном числе или трех взаимно перпендикулярных осей.

5.L3 может встречаться в единственном числе или с 4L3.

Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный кристалл.

Кристалл, имеющий форму куба, обладает высокой степенью симметрии. В нем присутствуют три оси симметрии четвертого порядка (3L4), проходящие через середины граней куба, четыре оси симметрии третьего порядка (4L3), проходящие через вершины трехгранных углов, и шесть осей второго порядка (6L2), проходящих через середины ребер. В точке пересечения осей симметрии располагается центр симметрии куба (С). Кроме того, в кубе можно провести девять плоскостей симметрии (9Р). Элементы симметрии кристалла можно изобразить кристаллографической формулой.

Для куба формула имеет вид: 9P, 3L4, 4L3, 6L2, C.