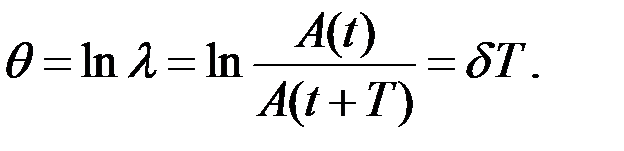Тема 7. Механические колебания. Пружинный маятник

Механическими колебаниями называются движения, характеризующиеся определенной повторяемостью во времени.

Колебания называютсясвободными (илисобственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармоническими колебанияминазываютсяколебания, при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса).

Пружинный маятник – это колебательная система, состоящая из груза массой т, закрепленного на пружине, и совершающая гармонические колебания под действием упругой силы 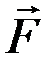, зависящей от величины линейной деформации x в соответствии с законом Гука: F_x = – kx, где k –жесткость пружины.

Согласно второму закону Ньютона уравнение движения маятника:

.

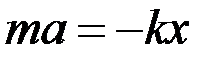Так как ускорение a является второй производной от смещения x ( 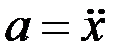), то

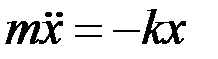или .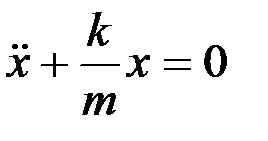

Если обозначить 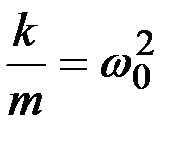, то получим дифференциальное уравнение свободных незатухающих гармонических колебаний пружинного маятника:

.

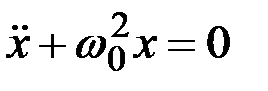Решением этого дифференциального уравнения является функция x(t):

,

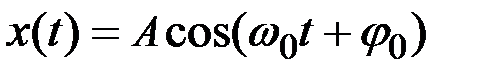где 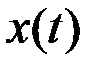– отклонение колеблющегося тела от положения равновесия в момент времени t;

А – амплитуда колебания, то есть максимальное отклонение колеблющегося тела от положения равновесия;

w₀ –круговая (циклическая) частота;

(w₀t+j₀) – фаза колебания в момент времени t;

j₀ –начальная фаза колебания.

Круговая частота ,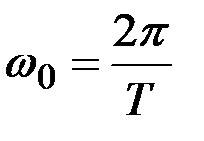

где Т – период колебаний, то есть время одного полного колебания.

Так как 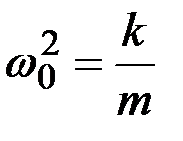, то период свободных незатухающих гармонических колебаний пружинного маятника .

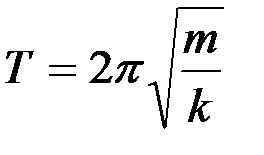Кинетическая энергия колебаний пружинного маятника:

.

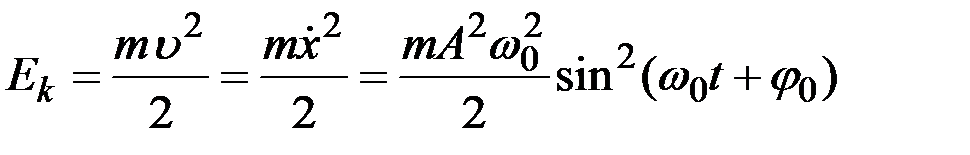Потенциальная энергияколебаний пружинного маятника:

.

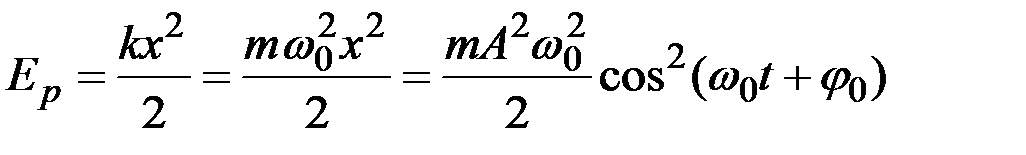Полная энергия колебаний пружинного маятника:

,

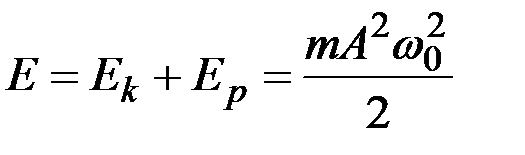откуда видно, что полная энергия свободных незатухающих гармонических колебаний пружинного маятника остается постоянной.

Свободные затухающие гармонические колебания пружинного маятника(рис. 6). Для пружинного маятника массой т, совершающего колебания под действием упругой силы 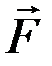(F_x = – kx)с учетомсилы сопротивления , пропорциональной скорости 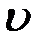движения груза ( 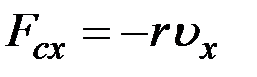), второй закон Ньютона имеет вид:

,

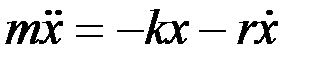где r – коэффициент сопротивления.

Обозначив 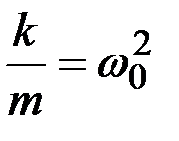и 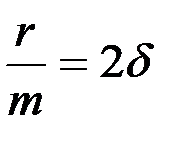( 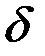– коэффициент затухания), получим дифференциальное уравнение свободных затухающих гармонических колебаний пружинного маятника:

.

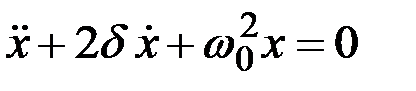Решением этого дифференциального уравнения в случае малых затуханий

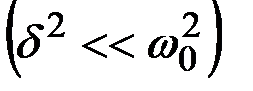является функция x(t):

,

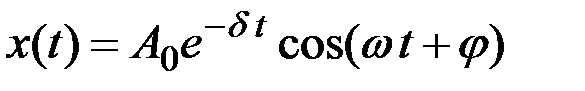где 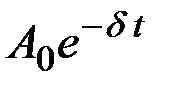– амплитудазатухающих колебаний в момент времени t;

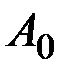– начальная амплитуда, т.е. амплитуда в момент времени t = 0,

– круговая (циклическая) частота: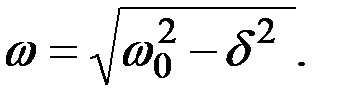

Периодзатухающих гармонических колебаний пружинного маятника:

.

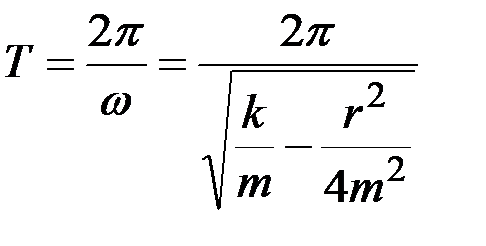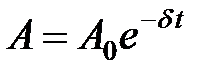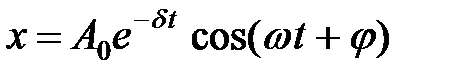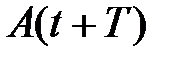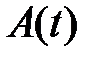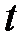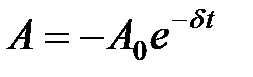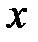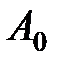T

Рис. 6

Декремент затухания. Если A(t)и А(t+Т) – амплитуды двух последовательных колебаний (рис. 6), то отношение этих величин называетсядекрементом затухания .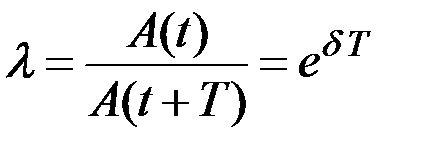

Логарифм 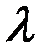называетсялогарифмическим декрементом затухания :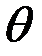