Колебательные состояния многоатомных молекул

В отличие от двухатомных гетероядерных молекул ИК спектр поглощения многоатомных молекул значительно сложнее. Это объясняется тем, что многоатомные молекулы имеют не одну, а по крайней мере 3 колебательных степени свободы, причем с ростом количества атомов в молекуле их число увеличивается.

Число колебательных степеней свободы n в зависимости от числа атомов в молекуле N определяется по формулам:

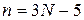(для линейных молекул) (56)

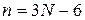(для нелинейных молекул) (57)

Эти выражения легко обосновать следующим образом.

У частиц одноатомного газа энергия распределена по трем поступательным степеням свободы. Если молекула образована из N атомов, она сохраняет 3N степеней свободы, которые имели N свободных атомов, однако распределяются они по различным видам молекулярного движения. Три из них будут приходиться на поступательное движение молекулы, две (для линейных) или три (для нелинейных) – на вращательное движение молекулы как целого. Остальные (3N - 5 или 3N - 6) приходятся на изменение формы молекулы, на ее изгибание или растяжение ее связей, т.е. на колебательное движение.

Колебания ядер молекулы представляют собой сложное явление. В классическом (т.е. основанном на законах классической механики) приближении, как и в случае двухатомных молекул, колебания многоатомных молекул при малых амплитудах можно считать гармоническими. На основании теории малых колебаний было показано, что любое сколь угодно сложное колебательное движение молекулы в гармоническом приближении можно разложить на n независимых движений, которые называются нормальными колебаниями. Каждое нормальное колебание совершается с определенной частотой ν_i, которая называется частотой данного нормального колебания, основной, или фундаментальной частотой.

Для описания колебательного движения молекулы вводят ЗN - 5 ил 3N - 6 колебательных координат. В качестве таких координат удобно выбрать величины, характеризующие изменение расстояний между ядрами и изменение углов между связями (по отношению к их равновесным значениям). Такая система внутренних координат получила название валентно-силовой системы координат, а сами коорди­наты - естественных колебательных координат q_i.

Так, для трехатомной нелинейной молекулы, имеющей 3 колебательных степени свободы (3∙3-6), можно ввести 3 колебательные координаты (рис. 15), две из которых отвечают изменению расстояний ХУ(q₁) и XZ (q₂), а третья – изменению утла между связями УXZ (q₃), т.е. молекула ХУZ имеет три нормальных колебания и, следовательно, три основных частоты колебаний.

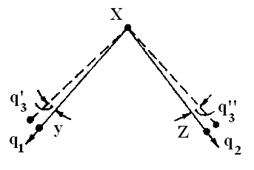
Рис.15. Внутренние колебательные координаты трёхатомной молекулы: q₁, q₂,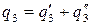

Величина и направление амплитуд смещения ядер для данного нормального колебания определяют его форму, исходя из которой, колебания разделяют на валентные (ν) и деформационные ( ) .

Валентными называют колебания, при которых в основном изменяются длины связей, а межсвязевые и другие углы остаются почти неизменными. Деформационными называют колебания, при которых в основном изменяются межсвязевые и другие углы, а длины связей изменяются мало.

И те и другие колебания могут быть симметричными (s) или антисимметричными (as) .

В качестве примера ниже схематически показаны колебания метиленовых (-СН₂) групп (а - симметричное, б - антисимметричное, в - ножничное, г - маятниковое, д - веерное, е - крутильное):

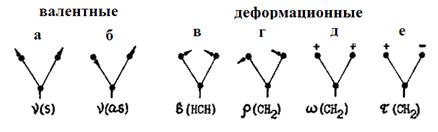
Чисто валентные и чисто деформационные колебания встречаются редко - только для линейных или высокосимметричных молекул. Для большинства молекул характерны смешанные колебания, в которых одновременно изменяются как длины связей, так и межсвязевые и другие углы.

Для молекул с низкой симметрией возможны только невырожденные колебания. Число различных частот нормальных колебаний в этом случае равно числу колебательных степеней свободы. В более симметричных молекулах некоторые нормальные колебания различной формы совершается с одинаковой частотой. Такие колебания называют вырожденными, а число таких колебаний - степенью вырождения. Колебания могут быть дважды или трижды вырожденными, причём в молекуле может быть несколько групп вырожденных колебаний.