Вращательные спектры поглощения двухатомных молекул

Чисто вращательные спектры наблюдаются в далекой ИК и микроволновой областях для веществ в газообразном состоянии в результате изменения только вращательной энергии молекул:

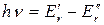(24)

Вращательный спектр поглощения двухатомного газа (рис. 7) представляет собой набор узких линий. Интенсивность поглощения в спектре проходит через максимум, причем разность волновых чисел 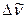между соседними линиями сохраняется приближенно постоянной почти на всем протяжении спектра.

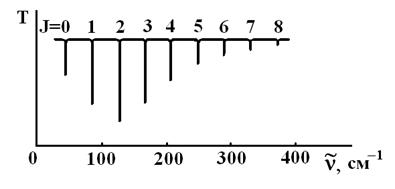
Рис. 7. Вращательный спектр поглощения HF при 298 К (схема)

При рассмотрении молекулы с точки зрения классической механики в качестве "жесткого ротатора", для которого равновесное межъядерное расстояние r_e=const, энергия вращения Е_r вокруг какой-либо оси прямо пропорциональна квадрату угловой скорости вращения ω:

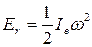(25)

где I_e-момент инерции, выраженный через r_e. Подстрочный индекс "е" - "equilibrium" - указывает, что рассматриваемые величины относятся к равновесной конфигурации молекулы, т.е. когда межъядерные силы притяжения равны силам отталкивания.

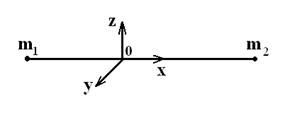
В общем случае молекула может иметь несколько ядер с массами m_i, удаленными от оси вращения на расстояния l_i, причем полное вращение можно разложить на вращения вокруг трех взаимно перпендикулярных осей. Тогда момент инерции относительно каждой оси

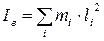(26)

Модель жесткого ротатора предусматривает, что момент инерции I_e данной молекулы остается постоянным, независимо от скорости и энергии вращения.

Если начало координат совпадает с центром тяжести молекулы 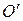, то моменты инерции I_x, I_у и I_z называются главными моментами инерции.

Для двухатомной молекулы имеются два равных по величине момента инерции относительно двух взаимно перпендикулярных осей, не совпадающих с осью молекулы: I_z = I_у = I_e, которые равны

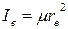(27)

где μ – приведённая масса молекулы – это такая эквивалентная масса, которая, будучи помещена на расстояние r_e от оси вращения, приводит к той же величине момента инерции, что и две массы m₁ и m₂ на расстоянии r_e. Приведённая масса выражается через массы ядер m₁ и m₂:

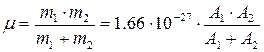(28)

где А₁ и А₂ – атомные массы ядер, а численный коэффициент перед дробью осуществляет перевод атомных единиц массы в кг.

Момент инерции I_x равен нулю из-за чрезвычайно малых собственных размеров ядер ( ):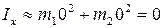

Для квантовомеханического описания вращательных энергетических состояний двухатомной молекулы необходимо составить и решить урав­нение Шредингера. Так как для жесткого ротатора r_e = const и, следовательно, U = 0, уравнение Шредингера можно записать в виде:

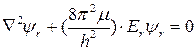(29)

При решении этого уравнения получается следующее выражение для собственных значений вращательной энергии E_r вокруг одной оси двухатомной молекулы:

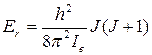(30)

где J-вращательное квантовое число, принимающее значения 0,1,2,3… Если разделить правую и левую части уравнения (11) на 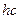, получим соотношение для вращательного терма F(J), выраженного в единицах волновых чисел:

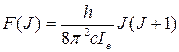(31)

Величина 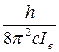, содержащая одну индивидуальную константу I_e, называется вращательной постоянной данной двухатомной молекулы и обозначается В_е, т.е.:

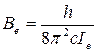(32)

Выражения для вращательной энергии и для вращательного терма в этом случае можно записать следующим образом:

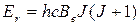(33)

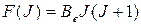(34)

Единицы измерения, в которых выражены вращательная постоянная В_e и вращательный терм F(J), определяются единицами, в которых выражены величины h, с и I_e. В единицах СИ величина В_e выражается в м^-1 и см^-1. В практических расчетах чаще используют см^-1.

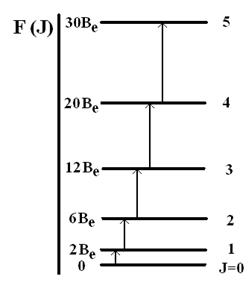Таким образом, Е_r не может принимать любые значения, и вращательные состояния молекулы описываются системой энергетических квантовых уровней с квантовыми числами J. Подставляя различные значения J в уравнение (30) или (31), можно найти вращательную энергию или вращательный терм для каждого уровня. Это соответствует системе расходящихся квантовых уровней на энергетической диаграмме (рис. 8).

Рис. 8. Диаграмма вращательных энергетических уровней двухатомной молекулы

Если рассматривать систему, состоящую из множества свободно вращающихся молекул, то равновесное распределение молекул по вращательным квантовым уровням при данной температуре носит статистический характер и обеспечивается тепловым движением молекул. При изменении температуры заселенность вращательных уровней меняется в соответствии с законом распределения Больцмана. Чем выше температура, тем более высокие уровни молекулярного вращения заселены.

Взаимное расположение вращательных уровней и их заселенность при данной температуре сильно зависят от момента инерции молекулы. Чем больше момент инерции, тем меньше величина В_е и тем ближе друг к другу располагаются вращательные уровни. Это видно на рис.9 для молекул HF, HI и СО.

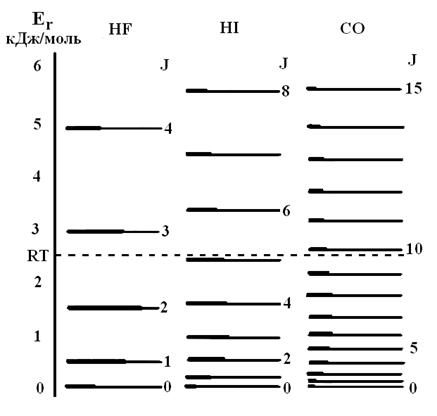
Рис. 9. Несколько низших вращательных уровней для молекул HF, HI и СО и относительная заселенность этих уровней (жирные линии) при 298 К. Моменты инерции: I_HF = 1.335∙10^-47 кг∙м²; I_HI = 4.295∙10^-47 кг∙м²; I_CO = 14.49∙10^-47 кг∙м²

При поглощении энергии переход 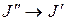возможен только между соседними уровнями, как это показано на рис. 8. Изменение энергии при вращательном переходе можно выразить в виде разности энергий верхнего и нижнего состоянии: 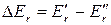. Пусть 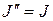, тогда 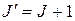и волновые числа вращательных переходов можно выразить уравнением:

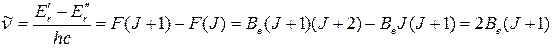(35)

Это и есть уравнение волновых чисел вращательного спектра поглощения, из которого следует, что первая линия (J=0) лежит при волновом числе 2В_е, вторая – при 4В_е, третья – при 6В_е и т.д. Таким образом, вращательный спектр поглощения двухатомной молекулы, рассматриваемой как жесткий ротатор, должен представлять собой серию равноотстоящих линий, а разность 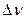между соседними линиями равна 2В_е:

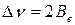(36)

что и наблюдается на опыте при небольших значениях волновых чисел (рис. 7). При увеличении волнового числа, т.е. при увеличении энергии вращения молекул, расстояние между линиями во вращательном спектре уменьшается, что связано с отклонениями от идеальной модели жёсткого ротатора. Интенсивность каждой линии поглощения пропорциональна числу молекул на уровне J, с которого произошел переход, а распределение интенсивности между отдельными линиями отражает заселенность различных уровней, в соответствии с законом распределения Больцмана (сравните относительную заселенность различных уровней для молекулы HF на рис. 9 и распределение интенсивности поглощения во вращательном спектре поглощения HF на рис. 7).

Для того, чтобы под действием электромагнитного излучения произошел вращательный переход, необходимо, чтобы молекула обладала постоянным дипольным моментом Р. Причина этого заключается в том, что переменное электромагнитное излучение способно взаимодействовать только с осциллирующим электрическим полем. Такое поле возникает при вращении молекулы с разделенными электрическими зарядами, т.е. диполя.

Отсюда следует, что чисто вращательные спектры поглощения можно наблюдать только для гетероядерных молекул (HСl, СО, NО и т.п.). Все же гомоядерные двухатомные молекулы (О₂, Н₂, С1₂ и т.п.) не спо­собны поглощать в далекой ИК и микроволновой областях спектра из-за отсутствия постоянного дипольного момента. Вращательные переходы для этих молекул можно изучать с помощью спектров комбинационного рассеяния.