Понятие о вращательных спектрах поглощения многоатомных молекул

В общем случае для многоатомных молекул необходимо учитывать все три главных момента инерции относительно трех осей координат. Главные моменты инерции в литературе нередко обозначаются как I_A, I_B и I_C, причем обозначение вводится так, чтобы соблюдалось условие: 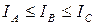. Им соответствуют вращательные постоянные .

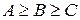В зависимости от соотношения между моментами инерции данной молекулы при рассмотрении вращательных спектров многоатомных молекул последние подразделяют на 4 типа (табл. 3)

Таблица 3. Классификация многоатомных молекул по моментам инерции

Тип молекулы	Момент инерции	Примеры
Линейная Сферический волчок Симметричный волчок Асимметричный волчок	Ix=0, Iy=Iz Ix=Iy=Iz Ix=Iy≠Iz Ix≠Iy≠Iz	HCN, N2O CH4, CCl4, SF6 NH3, CHCl3, C6H6 H2O, CH3OH, C2H3Cl

Линейные молекулы

Линейные молекулы обладают только двумя вращательными степенями свободы, соответствующими вращению относительно двух взаимно перпендикулярных осей – Y и Z.

Так как все ядра лежат на оси 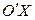, в соответствии с принятыми обозначениями можно записать, что I_x=I_A=0; I_y=I_z=I_В≠0

Квантовомеханическое выражение для энергии вращения здесь аналогично уравнению (30) для двухатомной молекулы.

Диаграмма вращательных энергетических уровней для линейных многоатомных молекул подобна диаграмме для двухатомных молекул (рис.7). Сохраняются те же правила отбора при вращательных переходах и внешний вид вращательного спектра, если молекула способна к поглощению.

Молекулы типа сферического волчка

Для этих молекул главные моменты инерции относительно трех пространственных осей координат равны и обозначаются обычно как I_В. Сюда относятся молекулы тетраэдрического и октаэдрического строения. Вращательные уровни молекул такого типа определяются тем же уравнением, что и для двухатомных молекул (уравнение (30), стр. 14).

Молекулы типа симметричного волчка

Поскольку для молекул этого типа два момента инерции равны, но отличаются от третьего, вращательный терм таких молекул усложняется и содержит две вращательные постоянные А и В и два вращательных квантовых числа J и К:

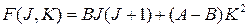(37)

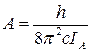где и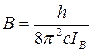

В этих выражениях I_A - момент инерции относительно оси симметрии молекулы, I_B - момент инерции относительно осей, перпендикулярных этой оси; J и К - вращательные квантовые числа, которые принимают значения целых чисел: К = 0, 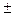1, 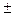2,...; J = К, К+1,К+2,... .

Молекулы типа асимметричного волчка

Это наиболее общий случай. Выражение для Е_r здесь усложняется, приходится вводить три вращательные постоянные. Вращательные спектры поглощения таких молекул чрезвычайно сложны.

Вращательные спектры поглощения многоатомных молекул наблюдаются только в том случае, если молекулы обладают постоянным дипольным моментом. По этой причине линейные симметричные молекулы (например, CO₂, CS₂, C₂H₄), все молекулы типа сферического волчка и некоторые молекулы типа симметричного волчка (например, C₆H₆) не дают чисто вращательных спектров поглощения.

Вращательные переходы неполярных многоатомных молекул можно наблюдать при колебательных переходах в результате поглощения в средней и ближней ИК областях, а также при изучении спектров комбинационного рассеяния.