Краткая теория классического эффекта Холла

Изучение эффекта Холла в полупроводниках

Цель работы: изучение эффекта Холла, определение концентрации носителей тока, изучение зависимости ЭДС Холла U_Н от индукции магнитного поля U_Н = f(B), построение картины распределения магнитного поля между полюсами электромагнита U_Н = f(Z).

Приборы и принадлежности: электромагнит, датчик Холла, блок питания, милливольтметр, амперметр.

Краткая теория классического эффекта Холла

Если к собственному полупроводнику приложить постоянную разность потенциалов Dj = U, то в нем возникнет упорядоченное движение зарядов: электронов и дырок (рис. 1).

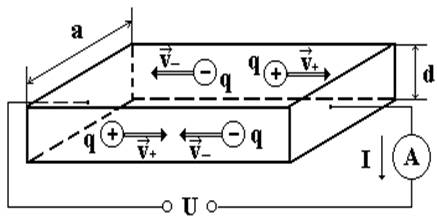Рис.14.1.

В результате через собственный полупроводник потечет постоянный электрический ток

I=n₊q₊v₊S + n_-q_-v_-S, (14.1)

где q₊ и q_- - заряды дырок и электронов, n₊ и n_­ - концентрации дырок и электронов, v₊ и v_- - дрейфовая скорость упорядоченного движения дырок и электронов соответственно, S = а×d - площадь поперечного сечения образца. В данной работе рассматривается полупроводник р-типа (дырочная проводимость). В связи с этим силу постоянного тока можно рассчитать по формуле

I = n₊q₊v₊ S. (14.2)

При внесении образца с током I в однородное постоянное магнитное поле с индукцией В (рис.2) на боковых гранях образца возникает разность потенциалов U_H, называемая ЭДС Холла (Hаll) [1]. Причиной ее появления является отклонение положительных зарядов (дырок) к одной из боковых граней образца под действием силы Лоренца F_л

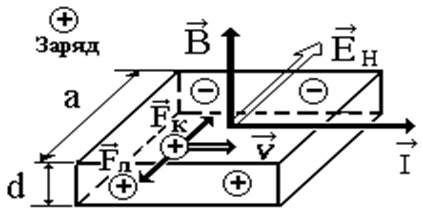Рис.14.2.

Причиной ее появления является отклонение положительных зарядов (дырок) к одной из боковых граней образца под действием силы Лоренца F_л

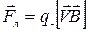. (14.3)

На противоположной боковой грани возникает избыточный отрицательный заряд. В результате этого в образце возникает внутреннее электрическое поле Е_Н, называемое полем Холла, напряженность которого связана с ЭДС Холла

U_H = E_H×a. (14.4)

Силы, действующие на дырки со стороны поля Холла

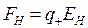(14.5)

направлены противоположно силе Лоренца и препятствуют движению дырок. В результате наступает динамическое равновесие сил:

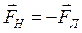(14.6)

Поскольку эти силы равны по величине и противоположны по направлению, то имеем 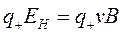, или

Е_Н = vB. (14.7)

Из (14.2) находим, что

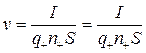. (14.8)

Из формул (4), (7) и (8) получаем выражение для ЭДС Холла:

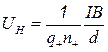(14.9)

или

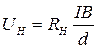(14.10)

Эффект Холла позволяет легко определить, каков знак и концентрация носителей в исследуемом веществе (это может быть как металл, так и полупроводник). С другой стороны, линейная зависимость Э.Д.С. Холла от В широко используется для измерения напряженности магнитного поля. Реально с помощью магнитометра на основе эффекта Холла можно измерять магнитные поля с чувствительностью ~ 10 Тл при температурах от ~ 0 К до ~ 1000 К. Тесламетры Холла применяются для контроля магнитных систем электроизмерительных и электронных приборов, для измерения магнитной индукции в зазорах электродвигателей, генераторов, электромагнитных реле, для измерения и анализа постоянных, переменных и импульсных магнитных полей.