Волновые свойства микрочастиц

Интерференция света

Скорость света в среде

V=c/n,

где с – скорость света в вакууме,

n – абсолютный показатель преломления среды.

Оптическая длина пути световой волны

L = n × l,

где l– геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода двух световых волн

D = L₁ – L₂=n₁l₁ – n₂l₂.

Связь разности фаз Dj световых волн с оптической разностью хода

Dj = (2p/l)×D .

Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пленки, находящейся в воздухе

,

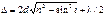где d – толщина пленки, i – угол падения.

Условие интерференционных максимумов

D = ± k×l или D= ± 2k ×(l/2), (k = 0,1,2,...).

Условие интерференционных минимумов

D = ± ( 2k + 1)×( l/2 ), (k = 0,1,2,...).

Дифракция света

Основные формулы:

Дифракция на одной щели.

При нормальном падении лучей на щель шириной a

условие дифракционных максимумов

a sin j = (2k+1) l/2 , (k=1, 2, 3 ...)

условие дифракционных минимумов

a sin j = kl , (k=1, 2, 3 ...)

Дифракция на плоской дифракционной решетке.

При нормальном падении лучей на решетку с периодом d

условие главных дифракционных максимумов

d sin j = k l , (k=1, 2, 3 ...)

условие добавочных минимумов

d sin j = k l/N ,

где N – число щелей (штрихов решетки), k = 1, 2, 3 ... , кроме значений k = N, 2N, 3N ...

Разрешающая способность дифракционной решетки

R = l/(d l) = kN,

где dl – наименьшая разность длин волн двух соседних спектральных линий (l и l +d l), при которой эти линии могут быть видны раздельно.

Угловая дисперсия дифракционной решетки

Dj = d j / dl = k / (d × cos j).

Линейная дисперсия дифракционной решетки

.

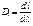Для малых углов дифракции D_l » F×D_j ,

где F – фокусное расстояние линзы, собирающей на экране дифракционную картину.

Поляризация света

Закон Брюстера tg a_о = n₂₁,

где a_о – угол падения, при котором отраженные световые волны полностью поляризованы; n₂₁ – относительный показатель преломления.

Закон Малюса J = J_o cos² a ,

где J – интенсивность света, прошедшего систему поляризатор–анализатор; J_o–интенсивность плоскополяризованного света, падающего на анализатор; a – угол между плоскостями пропускания поляризатора и анализатора.

Степень поляризации света

,

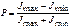где J_max и J_min – максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.

Угол поворота плоскости поляризации оптически активными веществами равен:

а) в твердых телах j = a× d,

где a – постоянная вращения, d – толщина слоя оптически активного вещества;

б) чистых жидкостях j = [a]×r d,

где [a] – удельное вращение, r – плотность жидкости;

в) в растворах j = [a]×с d,

где с – массовая концентрация оптически активного вещества в растворе.

Тепловое излучение

Закон Стефана-Больцмана

R_э = s T⁴,

где R_э – энергетическая светимость черного тела (энергия, излучаемая с единицы поверхности тела, в единицу времени, во всем спектральном интервале излучения); T – абсолютная температура тела; s – постоянная Стефана-Больцмана ( s = 5,67^.10^–8 Вт/(м^{2 .} К⁴) ).

Закон смещения Вина l_max = b΄/ T΄ ,

где l_max– длина волны, на которую приходится максимум излучательной способности тела; b΄ – постоянная Вина (b΄ = 2,9·10^-3 м·К ).

Второй закон Вина ( r_{l, T}) _max = b΄΄× T⁵ ,

где (r_{l, T})_max – максимальная излучательная способность (максимальная спектральная плотность энергетической светимости); b΄΄– вторая постоянная Вина (b΄΄=1,3 ^. 10^–5 Вт/ (м^{3 .} К⁵)).

Излучательная способность тела – это энергия, излучаемая нагретым телом в единицу времени, с единицы поверхности нагретого тела в узком спектральном интервале от l до (l + Dl ).

Связь между энергетической светимостью и излучательной способностью тела .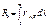

Закон Кирхгофа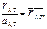

где 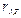– излучательная способность тела; 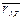– излучательная способность абсолютно черного тела; 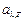– поглощательная способность тела.

Поглощательная способность тела – отношение энергии, поглощенной телом к энергии, падающей на тело, причем и та, и другая энергии берутся в единицу времени и приходятся на единицу поверхности нагретого тела.

Энергетическая светимость серого тела

R_э = а_T × s × T⁴,

где а_T– поглощательная способность серого тела.

Фотоэффект

Формула Эйнштейна:
hn = A + (m×u²_max)/2,

где e = hn – энергия фотона, падающего на поверхность металла; А – работа выхода электрона из металла; (m×u²_max )/2 – максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта n_о = А / h или
l_о = сh / A ,

где n_о – минимальная частота (l_о– максимальная длина волны), при которой еще возможен фотоэффект.

Условие наблюдения фотоэффекта hn ³ A .

Давление света

Давление, производимое светом при нормальном падении

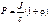
где J – интенсивность света (энергия, переносимая волной через единичную поперечную площадку в единицу времени); r – коэффициент отражения; с – скорость света в вакууме.

Для абсолютно черной поверхности r = 0.

Для абсолютно белой поверхности r = 1.

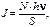
где N – число фотонов, падающих на поверхность площадью S за единицу времени; n – частота света.

АТОМ БОРА

Первый постулат Бора: электроны в атоме могут двигаться только по определенным орбитам, находясь на которых они не излучают энергии. Эти орбиты называются стационарными и определяются условием

mυ_nr_n=nћ, (1.1)

где r_n – радиус n-ой орбиты, υ_n – скорость электрона на этой орбите; mυ_nr_n – момент импульса электрона, n – главное квантовое число (n=1, 2, 3…), 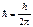, h – постоянная Планка, равная 6,62·10^-34 Дж·с.

Второй постулат Бора: при переходе электрона с одной орбиты на другую атом излучает или поглощает квант энергии, равный

hν=E_m-E_n, (1.2)

где E_m и E_n – энергии электрона на соответствующих орбитах.

Сериальная формула, определяющая длину волны света, излучаемого или поглощаемого атомом водорода при переходе из одного стационарного состояния в другое: 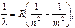(1.3)

где R – постоянная Ридберга, равная 1,097·10⁷ м^-1, nи m – целые числа, называемые квантовыми.

Квантовое число n определяет серию спектральных линий: n=1 – серия Лаймана (ультрафиолетовое излучение), n=2 – серия Бальмера (видимое излучение), n=3 – серия Пашена (первая инфракрасная серия), n=4 – серия Брэкета (вторая инфракрасная серия), n=5 – серия Пфунда (третья инфракрасная серия).

Сериальная формула для длин волн линий спектра водородоподобных ионов (т.е. ионов, имеющих по одному электрону: He⁺, Li⁺⁺ и т.д.) 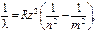(1.4)

где z – порядковый номер элемента в таблице Менделеева.

Для рентгеновских спектров выполняется закон Мозли, согласно которому положение линий определяется соотношением 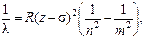(1.5)

где σ – постоянная экранирования, n=1 соответствует K-серии, n=2 соответствует L-серии, n=3 соответствует M-серии Для K-серии σ=1.

Коротковолновая граница λ_min сплошного рентгеновского спектра определяется формулой 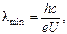(1.6)

где e – заряд электрона, U – напряжение в рентгеновской трубке.

ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ

Формула де-Бройля: ,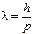

где λ – длина волны, связанная с частицей, имеющей импульс p=mυ.

Связь длины волны де-Бройля с кинетической энергией E_k имеет вид:

а) в классическом приближении (E_k<<m₀c²) p=mυ,

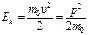
откуда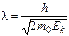

бб) в релятивистском случае (E_k~m₀c²)

E_k=mc²-m₀c²=E- m₀c²,

E²=( m₀c²)²+p²c²,

где Eи E_k – полная и кинетическая энергии соответственно. Таким образом, релятивистский импульс равен

,

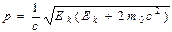соответственно

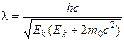
Соотношение неопределенностей:

для координаты и импульса

,

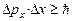где Δp_x – неопределенность проекции импульса частицы на ось x; Δх – неопределенность ее координаты;

2) для энергии и времени

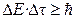
где ΔЕ – неопределенность энергии данного квантового состояния, Δτ – время пребывания системы в этом состоянии.