Космологическая постоянная, темная энергия и антропный принцип

Первой попыткой решить проблему космологической постоянной с помощью антропного принципа были работы (Linde, 1984b,1986b). Наиболее просто это можно сделать, рассмотрев инфляцию, вызванную скалярным полем 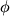(инфлатон), и сымитировав космологическую постоянную достаточно плоским потенциалом второго скалярного поля 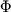. Простейший потенциал такого типа, линейный, имеет вид (Linde, 1986b)

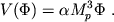
Если 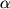достаточно мала ( 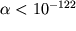), потенциал 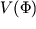является плоским настолько, что поле 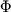практически не меняется на масштабах порядка 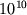лет, его кинетическая энергия очень мала, и на нынешнем этапе эволюции вселенной его полная потенциальная энергия ведет себя точно так же, как космологическая постоянная. Эта модель была одним из первых примеров того, что в дальнейшем было названо квинтэссенцией (quintessence), или темной энергией.

Однако плотность энергии поля 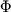, практически постоянная в настоящее время, должна была существенно меняться в процессе инфляции. Так как поле 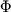- безмассовое, оно должно было испытывать квантовые скачки в произвольном направлении с амплитудой 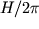на шкале времени 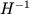. В контексте сценария вечной инфляции это значит, что квантовые флуктуации рандомизуют поле: вселенная оказывается разделенной на бесконечное число экспоненциально больших частей со всеми возможными значениями поля 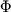. 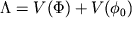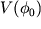Другими словами, вселенная разделяется на бесконечное число "вселенных" со всеми возможными значениями эффективной космологической постоянной , где - плотность энергии поля инфлатона 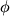в минимуме эффективного потенциала. Эта величина может меняться в пределах от 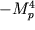до 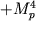в разных частях вселенной, но мы можем существовать только там, где 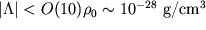, (здесь 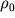означает современную плотность энергии в нашей части вселенной).

Действительно, если 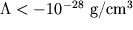, вселенная коллапсирует за время, существенно меньшее времени существования нашей вселенной ( 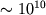лет) (Linde, 1984b,1986b; Barrow and Tipler, 1986). С другой стороны, при 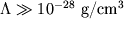вселенная в настоящее время должна была бы экспоненциально расширяться, плотность была бы экспоненциально малой, и жизнь известного нам типа была бы невозможна (Linde, 1984b,1986b). Это значит, что мы можем жить только в тех частях вселенной, в которых космологическая постоянная не слишком сильно отличается от наблюдаемого нами значения .

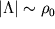Этот подход послужил основой для множества последующих попыток решить проблему космологической постоянной с помощью антропного принципа в рамках инфляционной космологии (Weinberg, 1987; Linde, 1990a; Vilenkin, 1995b; Martel et al, 1998; Garriga and Vilenkin, 2000,2001b,2002).

На первый взгляд, введение исчезающе малого параметра 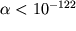не может служить удовлетворительным объяснением малости космологической постоянной 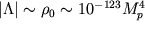. Однако, экспоненциально малые параметры могут естественным образом появляться из-за непертурбативных (nonperturbative) эффектов. Можно было бы даже решить, что подобные механизмы и являются причиной малости 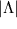, если бы не наличие других эффектов, дающих существенный вклад в эту величину - эффектов квантовой гравитации, спонтанного нарушения симметрии в GUT и электрослабых теориях, нарушения суперсимметрии, эффектов квантовой хромодинамики и других. Потому объяснение малости космологической постоянной посредством непертурбативных эффектов возможно, если только загадочным образом исчезают все остальные вклады, как, например, в модели, рассмотренной в прошлом абзаце. Но даже если вклады всех остальных эффектов исчезают, нам по-прежнему необходимо объяснить, почему принимаемое 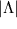значение таково, что соответствующая плотность энергии по порядку величины равна сегодняшней плотность энергии во вселенной. Проблема этого совпадения (называемая также coincidence problem) решается в вышеприведенной теории для всех достаточно малых 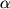; вместо тонкой ее подстройки нам надо лишь сделать ее достаточно малой. Очень ясное обсуждение выбора между тонкой подстройкой и экспоненциальным подавлением можно найти в работе (Garriga and Vilenkin, 2000) в приложении к похожей модель с потенциалом 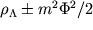с .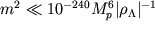

Альтернативные подходы, основанные на антропном принципе, описаны в работах (Bousso and Polchinski, 2001; Feng et al, 2001; Banks et al, 2001). Можно также использовать более общий подход и рассмотреть сценарий дочерней вселенной или Мультимир, состоящий из различных инфляционных вселенных с различными космологическими постоянными (Linde, 1989,1990a,1991). В этом случае нет необходимости в существенно плоском потенциале, однако процедура сравнения вероятностей оказаться во вселенных с различными 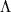значительно усложняется (Vilenkin, 1995; Garcia-Bellido and Linde, 1995). Однако, если сделать простейшее предположение о том, вселенные с различной величиной 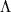равновероятны, получается антропное решение проблемы космологической постоянной без необходимости введения исчезающе малого параметра .

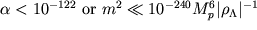Ограничение 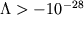г/см по-прежнему остается наилучшим нижним пределом на отрицательную космологическую постоянную; современное состояние вопроса см. в (Kallosh and Linde, 2002; Garriga and Vilenkin, 2002). Между тем предел на положительную космологическую постоянную 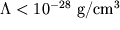был существенно улучшен в последующих работах.

В частности, Вейнберг обратил внимание на то, что процесс образования галактик идет лишь до того момента, когда плотность энергии космологической постоянной начинает доминировать, и вселенная входит в режим поздней инфляции (Weinberg, 1987). Рассмотрим, например, галактики, сформировавшиеся на 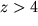, когда плотность энергии во вселенной была на 2 порядка больше нынешней. Они не могли бы образоваться при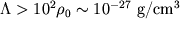

Следующий важный шаг был сделан в серии работ (Efstathiou, 1995; Vilenkin, 1995b; Martel et al, 1998; Garriga and Vilenkin, 2000,2001b,2002; Bludman and Roos, 2002). Авторы рассмотрели не только нашу галактику, но все галактики, в которых может быть жизнь нашего типа, что включает в себя не только уже существующие галактики, но также и те, что еще только формируются. Так как плотность вселенной на поздних стадиях эволюции вселенной уменьшается, даже очень малая космологическая постоянная может в какой-то момент положить предел дальнейшему образованию галактик или росту уже существующих. Это позволяет усилить ограничения на космологическую постоянную. Следуя работе (Martel et al, 1998), вероятность того, что астроном в произвольной вселенной обнаружит отношение 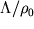близким к наблюдаемой нами величине 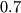варьируется от 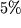до 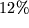в зависимости от предположений. В некоторых моделях, основанных на расширенной супергравитации, антропные ограничения могут быть еще более усилены (Kallosh and Linde, 2002).