Описание установки метода измерений
Для выполнения лабораторной работы необходимо познакомится еще с двумя изопроцессами – изотермическим и адиабатическим.
Изотермическим называется процесс, который совершается при постоянных температуре и массе газа, описывается процесс законом Бойля-Мариотта:
 (7.16)
(7.16)
Адиабатическим называется процесс, который совершается над газом без теплообмена с окружающей средой. Процесс описывается уравнением Пуассона:
 (7.17)
(7.17)
 Графики изопроцессов газов представлены на рис.7.2: АС – изотерма в координатах
Графики изопроцессов газов представлены на рис.7.2: АС – изотерма в координатах  -
-  , АВ– адиабата в координатах
, АВ– адиабата в координатах  -
-  .
.

 |
Рисунок 7.2
В адиабатическом процессе давление падает быстрее, чем в изотермическом, при одинаковом изменении объема в обоих процессах. Для определения отношения теплоемкостей газа 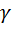 реализуется адиабатический процесс при помощи прибора Клемана-Дезорма.
реализуется адиабатический процесс при помощи прибора Клемана-Дезорма.
Сущность метода Клемана-Дезорма состоит в том, что некоторую массу газа, близкого по свойствам к идеальному газу, путем адиабатического расширения (адиабата АВ на рис 7.2) и изохорического нагревания (изохора BC, V=const) переводят из одного состояния (  ) в другое состояние (
) в другое состояние (  ). Но состояние газа с параметрами
). Но состояние газа с параметрами  характеризует и перевод газа по изотерме из состояния
характеризует и перевод газа по изотерме из состояния  (т.А).
(т.А).
Таким образом, в состоянии С можно перевести газ двумя изопроцессами:
1) изотерма  ;
;
2)адиабата  c изохорой.
c изохорой.
Уравнение изотермы возводим в степень γ:

Разделив уравнение (7.18) на уравнение (7.17), получим:
 =
=  (7.19)
(7.19)
Таким образом, измеряя давления газа, можно определить искомую величину γ.

Рисунок 7.3
Для практической реализации метода адиабатического расширения используется баллон большой емкости. Горловина баллона закрыта используется с тремя отверстиями, в которых размещены три трубки с кранами (рис.7.3).Кран К соединяет баллон с атмосферой, кран  –с насосом Н. Третья трубка связывает баллон с водяным манометром М.
–с насосом Н. Третья трубка связывает баллон с водяным манометром М.
С помощью насоса в баллон накачивают воздух. Кран К должен быть закрытым. Накачивание воздуха происходит довольно быстро, поэтому воздух в насосе и, конечно, в баллоне разогревается.
Спустя некоторое время избыточная теплота перейдет к воздуху комнаты и установится тепловое равновесие, которое характеризуется комнатной температурой  и давлением
и давлением  ,где
,где  - давление воздуха в комнате, а
- давление воздуха в комнате, а  -показатель разностиуровней водяных столбов в манометре. Выделив мысленно некоторый исследуемый объем газа
-показатель разностиуровней водяных столбов в манометре. Выделив мысленно некоторый исследуемый объем газа  (состояние 1 изображено линией 1 на рис 7.3), получим его состояние, которое изображено точкой А(
(состояние 1 изображено линией 1 на рис 7.3), получим его состояние, которое изображено точкой А(  ) на диаграмме (см. рис.7.2).
) на диаграмме (см. рис.7.2).
Открывая кран К, соединяем баллон с комнатой. Процесс расширения газа происходит быстро, что приблизительно отвечает адиабатическому процессу. Выделенный объём газа перейдет в состоянии 2(на диаграмме рис.7.2 точка В). Его объем  (состояние 2 изображено пунктирной линией 2 в баллоне на рис.7.3) больше, чем
(состояние 2 изображено пунктирной линией 2 в баллоне на рис.7.3) больше, чем  давление
давление  равняется комнатному, температура
равняется комнатному, температура  ниже комнатной, так как газ выполнил работу адиабатического расширения.
ниже комнатной, так как газ выполнил работу адиабатического расширения.
После окончания процесса адиабатического расширения кран К перекрывается и газ в баллоне нагревается, получая тепло из комнаты. Спустя некоторое время температура газа в баллоне станет равной комнатной, выделенный объем перейдёт в состояние 3 (на рис.7.2 точка С(  )).
)).
Этот объём станет равным объёму в состоянии 2,а давление  , где
, где  -разность уровней в коленах манометра после достижения равновесного состояния газа в баллоне.
-разность уровней в коленах манометра после достижения равновесного состояния газа в баллоне.
Используя уравнения (7.19), получаем:
 (7.20)
(7.20)
После преобразования уравнения (7.20), получим:

После сокращения на  и логарифмирования получим:
и логарифмирования получим:
 )ln(
)ln(  ).(7.21)
).(7.21)
Отношение  –малая величина , так как
–малая величина , так как  –около десятка сантиметров водяного столба, а
–около десятка сантиметров водяного столба, а  имеет около760 ммртутного столбика, или 760·13,6=10366 мм водяного столба. Поэтому при разложении в ряд логарифмов можно ограничиться величинами первой степени малости:
имеет около760 ммртутного столбика, или 760·13,6=10366 мм водяного столба. Поэтому при разложении в ряд логарифмов можно ограничиться величинами первой степени малости:
ln( 
что даст возможность переписать уравнение (7.21):
 )
)  ,
,
откуда
 .(7.22)
.(7.22)
Значения  и
и  поддаются прямым измерениям, и формула (7.22) является расчетной для определения отношения теплоёмкостей воздуха при постоянном давлении и постоянном объёме.
поддаются прямым измерениям, и формула (7.22) является расчетной для определения отношения теплоёмкостей воздуха при постоянном давлении и постоянном объёме.
