Элементы квантовой механики

Квантовая механика изучает поведение микрочастиц при размерах их движения порядка размеров атома, т.е. в тех случаях, когда классическая механика к частицам неприменима.

1. Согласно идее Л. де Бройля любая частица подобно фотону обладает волновыми свойствами и имеет длину волны

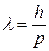
где 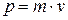– импульс частицы, m – масса частицы, v – ее скорость.

2. Наличие волновых свойств у микрочастиц не позволяет использовать для описания их поведения законы классической механики. Квантовая механика утверждает, в частности, что в отличие от классической частицы микрочастица не может иметь одновременно точно определенные координату и импульс. Согласно соотношению неопределенностей:

,

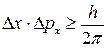где Δx – неопределенность (абсолютная погрешность)координаты частицы, Δp_x - неопределенность (абсолютная погрешность) проекции импульса частицы на ось ОХ, h – постоянная Планка.

3. Аналогичное соотношение можно записать и для неопределенностей энергии ΔW и промежутка времени Δt, в течение которого измеряется энергия:

.

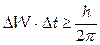Пример.

Электрон находится в атоме, размер которого примерно равен 0,3 нм и имеет скорость 2·10⁶ м/с. Определить: 1) длину волны де-Бройля электрона; 2) относительную погрешность, с которой рассчитывается скорость электрона.

Решение

1) Длина волны де-Бройля для электрона

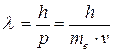
Из справочника масса электрона 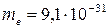кг. Тогда

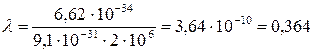нм.

2) Минимальная неопределенность (абсолютная погрешность) импульса может быть найдена из соотношения неопределенностей:

.

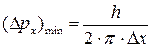Неопределенность координаты частицы в данном случае равна половине размера атома: 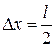. Таким образом,

.

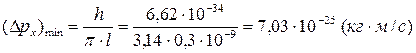Т.к. импульс 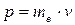, то минимальная абсолютная погрешность скорости

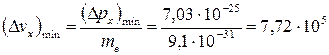(м/с).

Относительная погрешность скорости

%

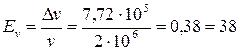Ядерная физика

1. Основную массу атомного ядра составляют нуклоны: протоны и нейтроны. Количество протонов N_р в ядре определяет его зарядовое число Z ( 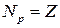). Заряд ядра равен 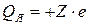, где е – величина элементарного заряда.

Общее количество нуклонов (протонов и нейтронов) определяется массовым числом ядра А. Следовательно, число нейтронов в ядре 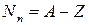. Масса ядра в атомных единицах массы (а.е.м.) .

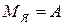Зарядовое и массовое числа Z и А можно найти из условного обозначения ядра:

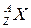или ,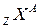

где Х – символ химического элемента.

Аналогично ядрам обозначаются элементарные частицы:

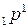- протон; 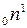- нейтрон; 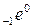- электрон.

2. Ядерные реакции – это процесс взаимодействия атомного ядра с элементарными частицами и ядрами других элементов, приводящий к преобразованию ядер. Пример записи ядерной реакции:

,

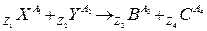где Х и Y – химические символы исходных компонентов;

В и С – химические символы продуктов реакции.

При протекании ядерной реакции выполняются законы сохранения:

– числа нуклонов ;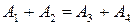

– заряда ;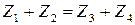

– релятивисткой полной энергии 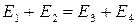, где ;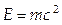

– импульса .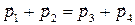

3. Радиоактивностью называется самопроизвольное превращение одних атомных ядер в другие, сопровождающееся испусканием радиоактивных излучений (α- , β- , и γ - лучей). При этом может наблюдаться:

– α-распад – испускание ядер гелия 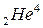(альфа-частиц). Схема протекания реакции

.

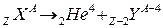– β-распад – испускание электронов 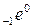или позитронов 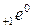(античастиц электрона), а также нейтральной частицы малой массы, называемой антинейтрино 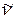или нейтрино ν, соответственно. Схема протекания реакции отрицательного (электронного) β-распада

.

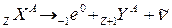– γ –распад – испускание квантов электромагнитного излучения с большой энергией. При γ –распаде зарядовое и массовое числа ядра не изменяются.

4. Основной закон радиоактивного распада:

,

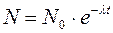где N – число нераспавшихся атомов в момент времени t, N₀ – число нераспавшихся атомов в начальный момент времени, е – основание натуральных логарифмов, λ – постоянная распада, зависящая от вида распадающегося вещества.

Количество атомов вещества можно найти, зная его массу m

,

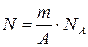где А – массовое число ядра, N_А – постоянная Авогадро.

Постоянная распада λ связана с периодом полураспада вещества Т : .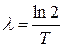

Тогда закон радиоактивного распада можно записать в виде

.

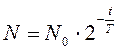Число атомов, распавшихся за время t можно найти .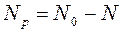

5. Активность а радиоактивного образца – это величина, показывающая, сколько атомов образца распадается в единицу времени, и численно равная отношению числа ядер dN, распавшихся в веществе за бесконечно малый промежуток времени dt, к величине этого промежутка (производной от N(t) по t)

.

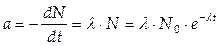6. Энергия связи атомного ядра – это энергия, которая выделяется при соединении свободных протонов и нейтронов в ядро.

,

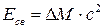где ΔМ – дефект массы, то есть разность масс отдельных протонов и нейтронов и образовавшегося из них ядра, с – скорость света в вакууме.

Удельная энергия связи – это энергия, приходящаяся на один нуклон.

,

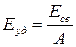где А – массовое число ядра.

Чем больше удельная энергия связи, тем больше устойчивость ядра.

Пример

Изотоп магния 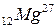испытывает отрицательный β-распад. Какой изотоп получается в результате этого распада? Какая часть от исходного количества атомов магния распадается за 1 час? Какова будет активность образца магния в этот момент времени, если его начальная масса 20 г? Период полураспада изотопа 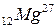равен 10 минут.

Решение:

1) Запишем реакцию отрицательного β-распада

.

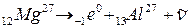Полученный неизвестный элемент с зарядовым числом 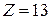находим по порядковому номеру в таблице Менделеева. Это изотоп алюминия .

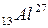2) Для нахождения доли нераспавшихся атомов изотопа в данном случае лучше использовать закон радиоактивного распада в виде

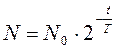
при этом время t и период полураспада Т должны быть выражены в одних и тех же единицах измерения. Например, если Т = 10 мин, то t = 1 час = 60 мин. Тогд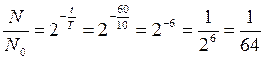а

, а .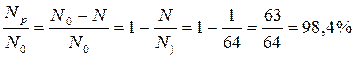

3) Активность 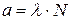. Зная начальную массу m₀ = 20 г = 0,02 кг, найдем начальное количество атомов изотопа 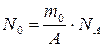, где массовое число А = 27; постоянная Авогадро 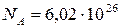кмоль^-1. Тогда ,

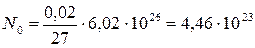а .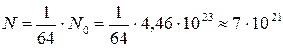

Постоянная распада 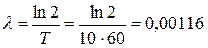с^-1. Тогда активность 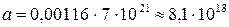расп/с 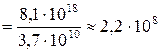Кu.

ПРИЛОЖЕНИЯ