Кинетические коэффициенты газов
1.5.1.Рассмотрим неоднородный по составу газ, находящийся при постоянных температуре и давлении, и пусть его состав меняется вдоль оси х. Вычислим с помощью поток частиц данного сорта через площадку площади А, перпендикулярную к оси х. Частицы, движущиеся со скоростями вблизи vi, будут давать в этот поток вклад

Полный же поток всех частиц рассматриваемого сорта, J, можно найти, просуммировав все возможные величины ji,. Это легко сделать, учитывая, что отношение  , где n—полная плотность числа частиц данного сорта, есть равновесная вероятность того, что частица движется со скоростью вблизи vi.
, где n—полная плотность числа частиц данного сорта, есть равновесная вероятность того, что частица движется со скоростью вблизи vi.
Первый член в правой частиц формулы обращается при суммировании в нуль:
 ,
,
поскольку  в случае максвелловского распределения. Вторую же сумму можно представить в виде
в случае максвелловского распределения. Вторую же сумму можно представить в виде
 ,
,
поскольку vix -- это заданная нами скорость, она не зависит от х, равно как и (возможно, зависящая от этой скорости) величина τi. Используя тот же прием, что прежде, получаем
 .
.
Последнее равенство справедливо, так как равновесное среднее  зависит только от температуры, а температура у нас однородна.
зависит только от температуры, а температура у нас однородна.
Сравнивая это выражение с законом Фика , получаем выражение для коэффициента диффузии:
 .
.
Если учесть качественный характер нашего рассмотрения, можно положить приближенно:  , где τ — среднее время пробега молекул всех скоростных групп. Тогда, учитывая, что
, где τ — среднее время пробега молекул всех скоростных групп. Тогда, учитывая, что  , получим
, получим
 ;
;
здесь  — средняя длина свободного пробега.
— средняя длина свободного пробега.
Из этих выражений видно, что коэффициент диффузии в газах растет при повышении температуры.
1.5.2.Предположим теперь, что, оставив постоянным давление, мы сделали температуру меняющейся вдоль оси х. Поток частиц и в этом случае определяется суммированием отдельных вкладов . И опять первый член при таком суммировании обратится в нуль. Результат же суммирования второго члена будет зависеть от того, зависит или не зависит от скорости время свободного пробега τi.
В однородном по составу газе столкновения, перемешивающие частицы разных скоростных групп, идут с участием всех частиц, находящихся в объеме V. Поэтому время установления равновесия, а, стало быть, и время свободного пробега, которое его определяет, в этом случае будет общим для всех них. Оно не будет (или почти не будет) зависеть от скорости данной частицы. От скорости будет зависеть длина свободного пробега:  .
.
Имея это в виду, суммирование второго члена в формуле можно представить в виде
 .
.
Но  , а пТ= Р, где Р— давление, одинаковое во всех точках газа. Поэтому
, а пТ= Р, где Р— давление, одинаковое во всех точках газа. Поэтому  . Мы видим, что наличие градиента температуры в однородном по составу газе не приводит к возникновению диффузионных потоков частиц, хотя плотность их числа,
. Мы видим, что наличие градиента температуры в однородном по составу газе не приводит к возникновению диффузионных потоков частиц, хотя плотность их числа,  , не однородна в пространстве.
, не однородна в пространстве.
Ситуация существенно меняется, если газ не однороден по составу. Рассмотрим для определенности поведение легких молекул, находящихся в виде примеси в газе, в основном, состоящем из тяжелых частиц [4]. Если легких частиц немного, их столкновениями друг с другом можно пренебречь. Основную роль в установлении их распределения по скоростям будут играть столкновения с тяжелыми частицами, скорость которых много меньше скорости легких молекул.
Сталкиваясь с такими, почти неподвижными тяжелыми частицами, легкие молекулы примеси будут менять только направление своей скорости, но не ее величину. Потому что удар будет почти упругий, и их энергия будет оставаться практически неизменной. Это значит, что группы легких молекул, имеющие разную величину скорости, не будут перемешиваться друг с другом. В каждой из них изотропное равновесное распределение по направлениям скорости будет устанавливаться независимо от установления равновесия в других группах.
Поэтому общим для всех легких частиц будет не время установления равновесия, не время свободного пробега, а длина свободного пробега λ. Время же пробега теперь будет зависеть от скорости  [5].
[5].
В таких условиях при суммировании второго члена в правой части формулы учтем, что 
 , а
, а  ,
,
где Θi — угол между направлением скорости vi, и осью х.
Тогда

последний шаг в этой цепочке равенств справедлив, поскольку направление случайной скорости vi, никак не связано с ее величиной. Далее, усредняя обе части соотношения:  по всем возможным направлениям и величинам скорости получим:
по всем возможным направлениям и величинам скорости получим:  , откуда следует, что
, откуда следует, что  , потому что
, потому что  . Таким образом, для полного потока легких частиц получаем
. Таким образом, для полного потока легких частиц получаем
 .
.
Если концентрация легких частиц, с=n/ntot, где ntot — плотность числа всех частиц газа, поддерживается постоянной вдоль оси х, то  , поскольку ntot = Р/Т. В этом случае зависимость произведения
, поскольку ntot = Р/Т. В этом случае зависимость произведения 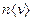 от х возникает только вследствие его зависимости от температуры. Поэтому можно записать
от х возникает только вследствие его зависимости от температуры. Поэтому можно записать
 .
.
Входящую сюда производную по температуре можно преобразовать так: поскольку  , a
, a 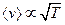 , то
, то  и
и
 .
.
Отсюда видим, что
 .
.
Коэффициент при  в этом выражении называют коэффициентом термодиффузии:
в этом выражении называют коэффициентом термодиффузии:
 .
.
Таким образом, при наличии градиента температуры легкие частицы будут диффундировать в направлении этого градиента, т.е. в сторону более высоких температур. И, если их концентрация, с, не поддерживается специально постоянной, как это будет, например, в случае газа, находящегося в замкнутом сосуде, разные стенки которого имеют разную температуру, легкие частицы начнут скапливаться в той части сосуда, где температура выше.
1.5.3.Чтобы определить коэффициент теплопроводности, нужно вычислить поток энергии, переносимый частицами при наличии градиента температуры. Вклад в этот поток от частиц i-й группы получится просто умножением их потока ji, даваемого формулой , на энергию частицы, εi:
 .
.
Будучи просуммирован по всем i, первый член в правой части этого выражения даст нуль, поскольку  — это равновесная максвелловская плотность частиц, а в равновесном газе все потоки в среднем равны нулю. При суммировании же второго члена будем полагать газ однородным по составу и считать поэтому, что τi не зависит от скорости частицы. Тогда получим
— это равновесная максвелловская плотность частиц, а в равновесном газе все потоки в среднем равны нулю. При суммировании же второго члена будем полагать газ однородным по составу и считать поэтому, что τi не зависит от скорости частицы. Тогда получим
 .
.
Теперь мы можем, во-первых, расщепить  на произведение
на произведение  , потому что это сильно упростит дело и не очень ухудшит ответ ввиду приближенности всего нашего подхода. Учтем, далее, что
, потому что это сильно упростит дело и не очень ухудшит ответ ввиду приближенности всего нашего подхода. Учтем, далее, что  не зависит от координаты, a
не зависит от координаты, a  зависит только потому, что от координаты зависит температура, так что
зависит только потому, что от координаты зависит температура, так что  . И, наконец, вспомним, что
. И, наконец, вспомним, что  есть теплоемкость на одну частицу. Тогда для потока тепла получим
есть теплоемкость на одну частицу. Тогда для потока тепла получим
 .
.
Сравнивая это выражение с законом Фурье , для коэффициента теплопроводности получим следующие оценки:
 .
.
На последнем шагу мы воспользовались соотношением  .
.
1.5.4.Для вычисления вязкости найдем поток у-компоненты импульса частиц. Вклад в этот поток от частиц i-й группы получится умножением потока частиц, ji, из на mviy. При суммировании этих вкладов, действуя совершенно так же, как в предыдущих случаях, получим
 .
.
После чего, учтя, что х- и у-компоненты скорости статистически независимы и что произведение  не зависит от координат, получим
не зависит от координат, получим
 .
.
Сравнивая это выражение с законом Ньютона , получим для вязкости следующие оценки:
 .
.
1.5.5.Последние равенства в формулах и показывают, что вязкость и теплопроводность газов растут с температурой, а при заданной температуре не зависят от плотности газа или от его давления. Независимость от плотности или давления получается в предположении, что  . Она будет сохраняться до тех пор, пока длина свободного пробега лимитируется столкновениями молекул. Но при уменьшении плотности величина λ, рано или поздно неизбежно становится порядка размеров сосуда, после чего ее рост прекращается. С этого момента и вязкость, и теплопроводность начнут уменьшаться при дальнейшем уменьшении плотности.
. Она будет сохраняться до тех пор, пока длина свободного пробега лимитируется столкновениями молекул. Но при уменьшении плотности величина λ, рано или поздно неизбежно становится порядка размеров сосуда, после чего ее рост прекращается. С этого момента и вязкость, и теплопроводность начнут уменьшаться при дальнейшем уменьшении плотности.
Отметим для полноты, что температурная зависимость теплопроводности и вязкости жидкостей, а также теплопроводности твердых тел носит прямо противоположный характер. При увеличении температуры все эти коэффициенты уменьшаются. Для теплопроводности твердого тела это справедливо, впрочем, лишь при не слишком низких температурах, когда его теплоемкость остается практически постоянной.
Такое различие связано с тем, что передача энергии или импульса в этих объектах осуществляется, в основном, не переносом частиц, а их силовым взаимодействием друг с другом. Но при повышении температуры связь между частицами становится все более и более слабой: твердое тело рано или поздно начинает плавиться, а жидкость закипает. Поэтому теплопроводность и вязкость уменьшаются.
