Основное уравнение пиродинамики
Считая, что расширение пороховых газов в орудии происходит без теплообмена, т. е. адиабатически, на основании первого закона термодинамики можно получить основное уравнение пиродинамики, описывающее процесс расширения пороховых газов в орудии.
Для адиабатического процесса сумма работ SАi, совершаемых пороховыми газами, равна изменению их внутренней тепловой энергии:
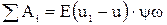 (2.1)
(2.1)
где u1 - внутренняя энергия 1 кг пороховых газов в момент их образования;
u - внутренняя энергия 1 кг пороховых газов в рассматриваемый момент времени;
E - механический эквивалент тепла.
Из термодинамики известно, что
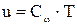 ,
,
где Cw - удельная теплоемкость пороховых газов при постоянном объеме;
Т - температура пороховых газов в градусах абсолютной шкалы.
Для момента образования пороховых газов будем иметь
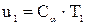
Тогда уравнение 2.1 получит вид
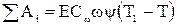 (2.2)
(2.2)
Воспользуемся еще одним соотношением термодинамики
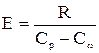
где R - удельная газовая постоянная;
Cp - удельная теплоемкость пороховых газов при постоянном давлении.
Введем параметр расширения пороховых газов q, определяемый равенством
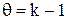 (2.3)
(2.3)
в котором k представляет собой показатель адиабаты
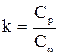 (2.4)
(2.4)
Можно записать
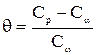
Величина q численно равна отношению работ расширения газов при изобарном и при адиабатическом термодинамических процессах. Выражение для Е примет вид
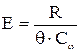 (2.5)
(2.5)
Подставив величину Е в уравнение 2.2, получим
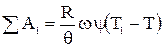 (2.6)
(2.6)
Раскрывая скобки и учитывая, что f = RT1, будем иметь
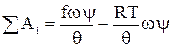 (2.7)
(2.7)
Произведение RT заменим с помощью уравнения состояния
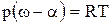 ,
,
в котором удельный объем пороховых газов при движении снаряда будет определяться равенством
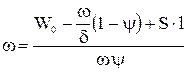 .
.
Используя, кроме того, выражение 2.4 из лекции № 4 для приведенной длины свободного объема каморы ly, найдем
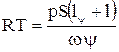 (2.8)
(2.8)
С учетом этого равенства уравнение 2.7 получит вид
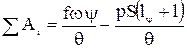 (2..9)
(2..9)
Полученное уравнение называется основным уравнением пиродинамики.
Это уравнение выражает собой закон сохранения энергии при выстреле. Оно записывается для произвольного момента времени, когда сгорит y-я часть порохового заряда, а снаряд пройдет путь l и будет иметь скорость V. В правой части стоит разность внутренней энергии образовавшихся пороховых газов до их расширения и после расширения (выражена в единицах работы). В левой части стоит механическая работа, которую совершают пороховые газы к рассматриваемому моменту времени.
Сила пороха f определяет работоспособность 1 кг пороха, а произведение fwy - работоспособность сгоревшей части заряда при изобарном процессе расширения пороховых газов. При этом часть тепла, выделяемого сгоревшим порохом, будет тратиться на поддержание постоянного давления. При адиабатическом процессе расширения пороховых газов, который происходит в орудии, все тепло идет на совершение работы. Поэтому для получения величины тепловой энергии произведение fwy делится на параметр расширения q.
