Задачи для практических занятий и домашних заданий

На выполнение письменного зачетного задания отводится 2 часа (академических).

Задачи для практических занятий и домашних заданий.

№1. Тема: Тепловое излучение.

1.1. Имеются 2 абсолютно черных источника теплового излучения. Температура одного из них T₁=2500K. Найти температуру второго источника, если длина волны, отвечающая максимуму испускательной способности, на 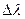=0,5мкм больше длины волны, соответствующей максимуму испускательной способности первого источника.

1.2. Раскаленная металлическая поверхность, площадью 10см² излучает в одну минуту 4·10⁴Дж энергии. Температура поверхности равна 2500K. Найти: 1) Каково было бы излучение этой поверхности, если бы она была абсолютно черной? 2)Каково отношение энергетических светимостей этой поверхности и абсолютно черного тела при данной температуре?

1.3. Мощность излучения АТЧ равна 10кВт. Найти площадь излучающей поверхности тела, если известно, что длина волн, на которую приходится максимум испускательной способности равна 750нм.

1.4. АЧТ находится при температуре Т₁=2900К. В результате остывания тела длина волны, на которую приходится максимум испускательной способности сместилась на 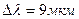. До какой температуры охладилось тело?

1.5. В результате нагревания АЧТ длина волны, соответствующая максимуму испускательной способности сместилась с λ₁ = 2,7 мкм до λ₂= 0,9 мкм. Определить во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная испускательная способность тела. Максимальная испускательная способность АЧТ возрастает по закону R(λ_m,T) = CT⁵, где С=1,3·10^-5Вт/м³к⁵

1.6. Определить, какая длинна волны соответствует максимальной испускательной способности способности R(λ_m,T), равна 1,3·10¹¹Вт/м³

1.7. Принимая солнце за черное тело и учитывая, что его максимальной испускательной способности соответствует длина волны 50нм, определить: 1) температуру поверхности солнца; 2)Энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) Массу, теряемую Солнцем за это время за счет излучения.

1.8. Использовав формулу Планка, определить спектральную плотность потока излучение с единицы поверхности АЧТ, приходящейся на узкий интервал длин волн Δλ = 5 нм. Вблизи максимум испускательной способности, если температура тела Т = 2500К

1.9. Какую мощность надо подводить к зачерненному металлическому шарику радиусом r = 2см., чтобы поддерживать его температуру на 27К выше окружающей среды, температура которой равна 20°С. Считать, что тепло теряется только вследствие излучения.

1.10. Показать, что при высокой температуре (кТ >>hυ) выражение для средней энергии <Е> переходит в классическое, т.е. <Е> = кТ; указание: использовать формулу Планка.

1.11. Определить, во сколько раз необходимо уменьшить термодинамическую температуру АЧТ, чтобы его энергетическая светимость R(T) уменьшилась в 16 раз.

1.12. Определить, во сколько раз изменится мощность излучения АЧТ, если длина волны, соответствующая максимуму его испускательной способности, сместилась с λ₁ = 720 нм до λ₂ = 400 нм

1.13. Температура T верхних слоев звезды Сириус равна 10 кК. Определить поток энергии Ф, излучаемый с поверхности площади S = 1 км²

1.14. С поверхности сажи площадью S = 2 см² при температуре Т = 400 К за время t = 5 мин излучается энергия W = 83 Дж. Определить коэффициент черноты a_т сажи.

№2. Тема: Фотоэлектрический эффект.

2.1. Определить красную границу фотоэффекта для цинка и максимальную скорость фотоэлектронов, вырываемых с его поверхности электромагнитным излучением с длиной волны 250 нм. Работа выхода А=3,74 эВ.

2.2. При поочередном освещении поверхности некоторого метала светом с λ₁ = 0,35 мкм и λ₂ = 0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в ŋ = 2 раза. Найти работу выхода с поверхности этого метала.

2.3. При увеличении напряжения на рентгеновской трубке в ŋ = 1,5 раза длина волны коротковолновой границы сплошного рентгеновского спектра изменилось на Δλ = 26 пм. Найти первоначальное напряжение на трубке.

2.4. Освещая поочередно фотокатод двумя разными монохроматическими источниками, находящихся на одинаковых расстояниях от катода, получим две зависимости фототока. Объяснить, в чем отличие этих источников.

2.5. Определить максимальную скорость электронов, вылетающих из металла под действием излучения с длинной волны с λ = 3*10^{-12 м.}

Указание: электрон считать релятивистской частицей, т.е. учитывать зависимость его массы от скорости: .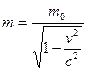

2.6. Определить, до какого потенциала зарядится уединенный серебряный шарик при его облучении ультра фиолетовым светом длинной волны λ = 208 нм. Работа выхода А=4,7эВ.

2.7.Найти длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость электронов, подлетающих к антикатоду трубки, v = 0,85 с.

2.8. На рисунке представлены вольтамперные характеристики (1-3) фотоэффекта для одного и того же метала объяснить причину отличия этих кривых.

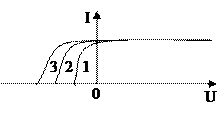
2.9. Определить максимальную скорость V_max фотоэлектронов, вырываемых с поверхности цинка (А = 4 эВ), при облучении γ – излучением с длиной волны λ = 2,47 пм.

2.10. Определить для фотона с длиной волны λ = 0,5 мкм.: 1) его энергию; 2) импульс; 3) массу.

№ 3. Тема : Давление света. Эффект Комптона.

3.1. Давление света, производимое на зеркальную поверхность, составляет 1мПа. Какова концентрация фотонов, падающих на поверхность, если длина волны света λ = 0,6 мкм.

3.2. Давление монохроматического света с длиной волны λ = 500 нм. На зачерненную поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фотонов, падающих ежесекундно на 1м² поверхности

3.3. Фотон с длиной волны λ₁ = 12,6 пм. Рассеян на свободном электроне. Длина волны рассеянного фотона λ₂ = 15 пм. Определить угол рассеяния фотонов.

3.4. Фотон в эффекте Комптона был рассеян на угол θ = π. Определить энергию, приобретенную электроном, если энергия фотона до рассеяния была 0,51 МэВ.

3.5. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20%.

3.6. Пучок параллельных лучей монохроматического света с λ = 663 нм падает нормально на зеркальную поверхность. Поток излучения Ф = 0,6 Вт. Определить силу давления на эту поверхность F и число n фотонов, ежесекундно падающих на нее.

3.7. Каково максимальное изменение длинны волны при комптоновском рассеянии света на свободных электронах и свободных протонов?

3.8. В результате эффекта Комптона фотон с энергией ε = 0.51 МэВ рассеян на угол θ = 120°. Определить энергию рассеянного фотона.

3.9. Какая доля энергии фотона приходится в эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол 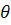= 180 . Энергия фотона до рассеяния составила 0,255 МэВ.

3.10. Длина волны λ фотона равна комптоновской длине волны λ_с электрона. Определить энергию и импульс фотона.

№4. Тема: Атом водорода по Бору.

4.1. Определить силу электрического тока, обусловленного движением электрона по первой Боровский орбите. Масса электрона m_e = 9.1 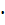10^{-31 кг, заряд |}e| =1.6 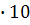^-19 Кл.

4.2. На какую величину изменится потенциальная энергия электрона, переходящего в атоме водорода с 1-ой на 4-ую боровскую орбиту? Во сколько раз изменится кинетическая энергия при обратном переходе на первую?

4.3. Вычислить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый?

4.4. Определить длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализируйте результаты.

4.5. Основываясь на том, что энергия ионизации атома водорода E_i = 13,6 эВ, определить в электрон-вольтах энергию фотона, соответствующую самой длинноволновой линии серии Бальмера.

4.6. Атом водорода испускает квант света при переходе его электрона с четвертой орбиты на вторую. Может ли этот квант света вырвать электрон с поверхности пластины из калия, работа выхода для которого A=2эВ?

4.7. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).

4.8. Из атома водорода, находящегося на втором энергетическом уровне, в результате поглощения фотона вылетает электрон, кинетическая энергия которого вдали от ядра равна 10 эВ. Определить энергию фотона в электрон-вольтах.

4.9. Фотон с энергией E = 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость V будет иметь электрон вдали от ядра атома?

4.10. Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном, энергия которого E = 17,7 эВ. Определить скорость V электрона за пределами атома.

№5. Тема: Волны де-Бройля. Соотношения неопределенностей.

5.1. Определить длину волны де-Бройля для электрона, находящегося в атоме водорода на 3-ей боровской орбите.

5.2.Найти длину волны де-Бройля для электрона, кинетическая энергия которого равна: 1) W_k1=100эВ; 2)W _k2= 3МэВ. Указания: 1) электрон – классическая частица; 2) электрон – релятивисткая частица.

5.3. Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10^{-5 м и пылинки массой} m = 10^{-12 кг, если её координата установлена с такой же точностью.}

5.4. Используя соотношение неопределенностей, доказать, что ядра атомов не могут содержать электроны. Радиус ядра принять равным 10 ^-15 м.

5.5. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния 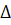t = 10^-8 с, определить отношение естественной ширины энергетического уровня, на котором был возбужден электрон, к энергии, излученной атомом.

5.6. Какую ускоряющую разность потенциалов U должен пройти электрон, чтобы длина волны де - Бройля была равна 0,1 нм?

5.7. Найти длину волны де Бройля для электрона, находящегося на второй орбите атома водорода?

5.8. С какой скоростью движется электрон, если длина волны де Бройля равна его комптоновской длине волны λ_с ?

5.9. Воспользовавшись соотношением неопределенностей, оценить размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния ( время его жизни равно 10 ^-8 с)

5.10. Используя соотношение неопределенностей, оценить ширину L одномерной потенциальной ямы, в которой минимальная энергия электрона равна 1эВ.

№6. Тема: Уравнение Шредингера.

6.1. Волновая функция, описывающая некоторую частицу, может быть представлена в виде Ψ(x,t)=ψ(x,t) 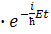. Показать, что плотность вероятности нахождения частицы определяется только координатой ψ-функции

6.2. Электрон находится в потенциальной яме шириной L. В каких точках интервала (0<x<L) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить значение плотности вероятности для этих точек. Решения пояснить графиком.

6.3. Ψ – функция некоторой частицы имеет вид Ψ = 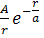, где r – расстояние этой частицы до силового центра; 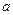– некоторая постоянная. Используя условия нормировки вероятностей, определить нормировочный коэффициент A.

6.4. Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной L. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n=2), будет обнаружен в средней трети ящика. Решение пояснить графиком.

6.5.Получить выражение для собственных значений энергии E_n частицы, находящейся в бесконечно глубокой одномерной потенциальной яме шириной L (решить уравнение Шредингера).

6.6. Получить выражение для собственных значений волновой функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме шириной L (решить уравнение Шредингера).

6.7. Частица в потенциальной яме шириной L находится в возбужденном состоянии с n=2. Определить, в каких точках интервала (0<x<L) плотность вероятности нахождения частицы имеет максимальное и минимальное значения.

6.8. Используя условия нормировки вероятностей определить нормировочный коэффициент A волновой функции Ψ = A 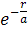, описывающей основное состояние электрона в атоме водорода, где r – расстояние электрона от ядра, a – первый боровский радиус.

6.9. Известно, что собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и шириной L, имеет вид Ψ_n(x)= 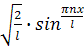. Определить среднее значение координаты <x> электрона.

6.10.Электрон находится в одномерной прямоугольной потенциальной яме шириной L с бесконечно высокими стенками. Определить вероятность P обнаружения электрона в средней трети ямы, если электрон находится в возбужденном состоянии (n=3). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

№7. Тема: Строение атомного ядра. Энергия связи.

7.1. Определить удельную энергию связи ядра атома гелия ⁴₂He. Масса нейтрального атома гелия равна 6,6467·10^{-27 кг.}

7.2. Определить дефект массы и энергию связи ядра атома тяжелого водорода ³₁H.

7.3. Атомное ядро, поглотившее γ-фотон (λ=0,47 пм),пришло в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия Т нуклонов равна 0,4 МэВ. Определить энергию связи ядра.

7.4. Определить порядковый номер Z и массовое число A частицы, обозначенной буквой X, в символической записи ядерной реакции ¹⁴₆C + ⁴₂He → ¹⁷₈O + X. Вычислить энергетический выход этой реакции.

7.5. Вычислить энергию ядерной реакции

⁹₄B + ⁴₂He → ¹⁰₅B + ³₁H.

Освобождается или поглощается эта энергия?

* 7.6. Определить удельную энергию связи для ядра углерода ¹⁴₆C и сравнить ее с удельной энергией связи ядра ⁴₂He. Массы нейтральных атомов гелия и углерода соответственно равны 6,6467·10^{-27 кг и 19,9272·10-27 кг.}

7.7. Вычислить дефект массы и энергию связи ядра ¹¹₅B.

7.8. Определить массу m_a нейтрального атома, если ядро этого атома состоит из трех протонов и двух нейтронов и энергия связи E_св ядра равна 26,3 МэВ.

7.9. Определить порядковый номер Z и массовое число A частицы, обозначенной буквой X, в ядерной реакции

²⁷₁₃Al +X → ¹₁H + ²⁶₁₂Mg.

Вычислить энергетический выход этой реакции.

7.10. Вычислить энергию ядерной реакции

¹⁴₇ N + ⁴₂He → ¹⁶₈O + ²₁H.

Освобождается или поглощается эта энергия?

№8. Тема: Явление радиоактивности. Период полураспада. Законы смещения.

8.1. Определить постоянную радиоактивного распада λ для изотопов тория ²³⁹₉₀Th и йода ¹³¹₅₃I. Период полураспада этих изотопов соответственно равен: 1)7·10³ лет; 8 сут.

8.2. Определить, сколько ядер в 1 мг радиоизотопа церия ¹⁴⁴₅₈Ce распадается в течение времени: 1) t₁ = 1 сут; 2) t₂ = 1год. Период полураспада церия составляет T = 285 сут.

8.3. Какая часть начального количества атомов радиоактивного актиния ²⁸⁵₈₉Ac останется через 5 сут? Через 15 сут? Период полураспада актиния T = 10 сут.

8.4. Определить, во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за 3 года, если за год оно уменьшилось в 4 раза.

8.5. Определить активность A фосфора ³²₁₅P массой m = 1 мг. Период полураспада T = 14,3 сут.

8.6. Определить постоянную радиоактивного распада λ для изотопа урана ²³⁵₉₂U. Период полураспада T = 4·10⁹ лет.

8.7. За какое время t₁ распадается начального количества ядер радиоактивного изотопа, если период его полураспада T = 24 сут?

8.8. Какая часть начального количества атомов распадается за 1 год в радиоактивном изотопе тория ²³⁹₉₀Th с периодом полураспада T = 7·10³ лет?

8.9. Определить, какая часть (%) начального количества ядер радиоактивного изотопа останется нераспавшейся по истечении времени t, равного двум средним временам жизни τ радиоактивного ядра.

8.10. Определить начальную активность радиоактивного препарата магния ²⁷₁₂Mg массой m = 0,2*10^{-9 кг, а также его активность} A через 6 часов, если его период полураспада T = 10 мин.

Литература.

1. Взоров Н.Н. , Замша О.И. , Иродов И.Е. , Савельев И.В. Сборник задач, 1986.

2. Волькенштейн В.С. Сборник задач по общему курсу физики, 1979.

3. Трофимова Т.И. , Павлова З.Г. Сборник задач по курсу физики, 2001.

4. Иродов И.Е. Задачи по квантовой физике, 1991.

5. Чертов А.Г. Воробьев А.А. Задачник по физике, 1981.

6. Иродов И.Е. Задачи по общей физике, 2006.

7. Методические указания и контрольные задания по дисциплине «Физика», Ч. 3. Волновая и квантовая оптика. Физика атома и атомного ядра, 2001. Кононенко В.Д.