Производные некоторых функций

Производная от постоянной величины y = C

y’ = 0.

Производная от степенной функции y = x^μ

y’ = μx^μ-1.

В частности, y = 1/х; y’ = - 1/х²;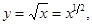

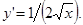
Производная от показательной функции y = а^х

y’ = a^x ln a.

В частности, y = е^х; y’ = е^х.

Производная от логарифмической функции y = log_ax

.

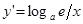В частности, для натурального логарифма y = ln x

y’ = 1/x.

Производная от тригонометрических функций:

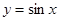
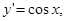
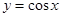
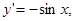
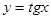
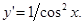
Производная от обратных тригонометрических функций:

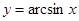
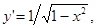
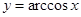
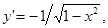
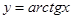
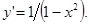
Таблица основных интегралов

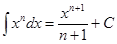(n≠ -1),

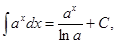если а = е, то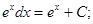

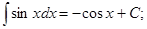
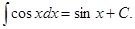
Работа выхода электронов из металла, эВ

Алюминий – 3,7 Вольфрам – 4,5 Литий – 2,3 Медь – 4,4

Платина – 6,3 Цезий – 1,8 Цинк – 4,0 Никель – 4,8

Периоды полураспада некоторых радиоактивных элементов

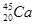- 164 суток 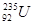- 7,1 ∙ 10⁸ лет

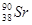- 27 лет 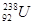- 4,5 ∙ 10⁹ лет

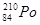- 138 суток 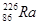- 1590 лет

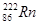- 3,82 суток 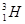- 12 лет

Элементы периодической системы и массы нейтральных атомов, а. е. м.

Элемент системы	Изотоп	Масса	Элемент системы	Изотоп	Масса
Водород   Гелий   Литий Бериллий Бор   Азот Кислород	- 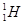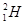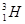-	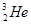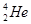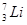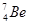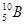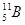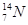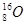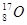1,00783 2,01410 3,01605   3,011605 4,00260 7,01601 7,01169 10,01294 11,00931 14,00307 15,99492 16,99913	Алюминий Кремний Фосфор Сера Железо Медь Вольфрам Магний   Кальций   Серебро Радий Торий Уран		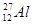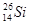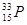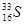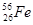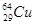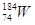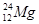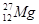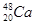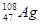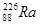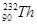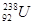26,98135 26,81535 32,97174 32,97146 55,94700 63,5400 183,8500 23,98504 26,98436 47,95236 107,869 226,0254 232,038 238,0508

О приближенных вычислениях

Числовые значения величин, которыми приходится оперировать при решении физических задач, являются большей частью приближенными. Поэтому при вычислениях нужно придерживаться следующих правил:

1. Достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных, так что с помощью вычислений невозможно получить результат более точный, чем исходные данные.

2. При сложении или вычитании чисел, имеющих различную точность, более точное должно быть округлено до точности менее точного. Например:

9,6 + 0,176 = 9,6 + 0,2 = 9,8; 100,8 – 0,4 = 100,4.

3. При умножении (делении) следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом значащих цифр. Например: 342 ∙ 378 = 129 ∙ 10³, но не 129276 и не 129300; 0,148 ∙ 0,183 = 7,65 ∙ 10^-3, но не 0,0076494; 0,350 : 3 = 0,117, но не 0,11667.

4. При извлечении корня n – степени, результат должен иметь столько значащих цифр, сколько их имеет подкоренное выражение. Например:

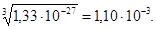
5. При вычислении сложных выражений соблюдаются правила в зависимости от вида производимых действий.

6. Когда число мало отличается от единицы, можно пользоваться приближенными формулами.

Если a, b, c – малы по сравнению с единицей (меньше 0,05), то

1) (1 ± а) (1 ± b) (1 ± с) = 1 ± а ± b ± с

2)

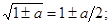
3) (1 ± а)ⁿ = 1 ± nа;

4) 1/(1 ± а)ⁿ = 1 ± аn;

5) 1/(1 ± а) = 1 ± а;

6) еⁿ = 1 + а;

7) ln (1 ± а) = ± а – а²/2.

7. Если угол α < 10⁰, то sin α = tg α = α (в радианах).

Соблюдая эти правила, студент сэкономит время на вычисление искомых величин при решении физических задач.