Теоретическое введение. ИЗУЧЕНИЕ ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНОГО СПЕКТРА ПОГЛОЩЕНИЯ МОЛЕКУЛЫ ЙОДА
ИЗУЧЕНИЕ ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНОГО СПЕКТРА ПОГЛОЩЕНИЯ МОЛЕКУЛЫ ЙОДА
Цель работы:Изучить закономерности электронно-колебательных спектров двухатомных молекул, определить характеристики электронно-колебательных переходов молекулы йода.
Приборы:Монохроматор УМ-2, ртутная лампа ДРШ-250, лампа накаливания, кювета с кристаллическим йодом, конденсор.
Задание
1. Изучить оптическую схему и принцип работы установки.
2. Используя ртутную лампу ДРШ-250, провести юстировку установки и градуировку монохроматора .
3. Получить отчетливый спектр поглощения молекул йода и изучить его структуру. 
4. Определить длины волн 5-7 полос поглощения йода и определить значения характеристик колебательного движения и энергии диссоциации молекулы иода в основном и возбужденном состояниях.
5. Изучить следующие вопросы:
· Классификация электронных состояний двухатомной молекулы.
· Колебательная структура электронных переходов.
· Принцип Франка-Кондона; следствие из него.
· Схема Деландра, парабола Кондона.
Теоретическое введение
Электронно-колебательные спектры поглощения или излучения молекул располагаются в видимой и ультрафиолетовой области и представляют собой совокупности полос. Полосы обычно имеют резкий край с одной стороны, называемый кантом полосы, и размытый – с другой. При регистрации такого спектра с помощью прибора с высокой разрешающей способностью обнаруживается колебательная структура электронной полосы, анализ которой позволяет определить ряд молекулярных параметров, характеризующих электронное и колебательное движения молекулы.
В данной работе исследуется спектр поглощения двухатомных молекул йода. Этот спектр находится в видимой области и представляет собой серию полос, сгущающихся по мере уменьшения длин волн.
Последовательное описание структуры электронно-колебательного спектра молекул дает квантовая механика. С квантово-механической точки зрения полная энергия молекулы в определенном стационарном состоянии выражается следующим образом:
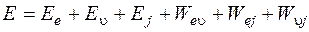 , (1)
, (1)
где 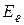 - энергия электронного движения молекулы (электронная энергия),
- энергия электронного движения молекулы (электронная энергия), 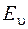 - энергия колебательного движения молекулы (колебательная энергия),
- энергия колебательного движения молекулы (колебательная энергия), 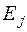 - энергия вращательного движения молекулы (вращательная энергия),
- энергия вращательного движения молекулы (вращательная энергия), 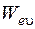 ,
, 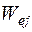 ,
, 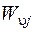 - энергии, учитывающие взаимное влияние электронного и колебательного, электронного и вращательного, колебательного и вращательного видов движения молекулы, соответственно.
- энергии, учитывающие взаимное влияние электронного и колебательного, электронного и вращательного, колебательного и вращательного видов движения молекулы, соответственно.
Электронная, колебательная и вращательная энергии квантованы. Для двухатомной молекулы правило квантования колебательной энергии в ангармоническом приближении имеет вид:

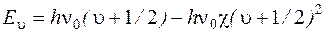 , (2)
, (2)
где 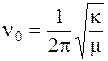 - собственная частота колебания молекулы,
- собственная частота колебания молекулы, 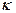 -силовая постоянная химической связи молекулы,
-силовая постоянная химической связи молекулы, 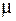 -ее приведенная масса,
-ее приведенная масса, 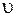 = 0,1,2,…. – колебательное квантовое число,
= 0,1,2,…. – колебательное квантовое число, 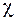 - параметр ангармоничности колебания.
- параметр ангармоничности колебания.
Как видно из формулы (2), с увеличением квантового числа 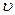 энергетическая разность между колебательными уровнями уменьшается.
энергетическая разность между колебательными уровнями уменьшается.
Квантование вращательной энергии двухатомной молекулы имеет вид:
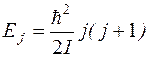 , (3)
, (3)
где j = 0, 1, 2, 3…; – вращательное квантовое число, I – момент инерции молекулы.
При переходе из одного стационарного состояния в другое могут изменяться все составляющие части энергии молекулы энергия излучаемого или поглощаемого кванта света будет равна:
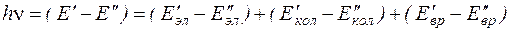 , (4)
, (4)
где один и два штриха, как принято в спектроскопии, относятся к верхнему и нижнему состояниям, соответственно.
Опыт и теория показывают, что 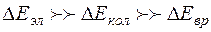 . В случае перехода молекул из одного электронного состояния в другое, т.е. в случае электронно-колебательных переходов, не существует строгого правила отбора для колебательного квантового числа
. В случае перехода молекул из одного электронного состояния в другое, т.е. в случае электронно-колебательных переходов, не существует строгого правила отбора для колебательного квантового числа 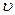 , и каждое колебательное состояние верхнего электронного состояния может комбинировать с каждым колебательным состоянием нижнего электронного состояния. Если учесть вращательные переходы, то получим, что каждому электронно-колебательному переходу будет соответствовать полоса, состоящая из большого числа близко расположенных линий.
, и каждое колебательное состояние верхнего электронного состояния может комбинировать с каждым колебательным состоянием нижнего электронного состояния. Если учесть вращательные переходы, то получим, что каждому электронно-колебательному переходу будет соответствовать полоса, состоящая из большого числа близко расположенных линий.
C учетом вышесказанного частота электронно-колебательного перехода в спектре поглощения (в пренебрежении вращательным движением) на основании формулы (4) определяется следующим образом:

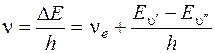 , (5)
, (5)
где 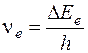 определяет изменение электронной энергии при данном переходе и определяет нулевую линию полосы. Нулевая линия каждой полосы соответствует переходу
определяет изменение электронной энергии при данном переходе и определяет нулевую линию полосы. Нулевая линия каждой полосы соответствует переходу 

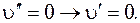
Используя (2) и (5), получим, что частоты электронно-колебательных переходов в поглощении могут быть вычислены по формуле:
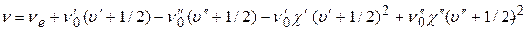 (6)
(6)
Здесь 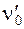 ,
, 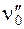 - частоты собственных колебаний молекулы в возбужденном
- частоты собственных колебаний молекулы в возбужденном 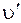 и основном
и основном 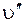 колебательных состояниях;
колебательных состояниях; 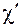 ,
, 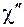 - параметры ангармоничности колебаний в соответствующих состояниях молекулы.
- параметры ангармоничности колебаний в соответствующих состояниях молекулы.
При невысоких температурах большая часть молекул находится на нижнем колебательном уровне основного состояния 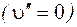 . Поэтому при поглощении соответствующих квантов практически имеются только переходы из нижнего колебательного состояния
. Поэтому при поглощении соответствующих квантов практически имеются только переходы из нижнего колебательного состояния 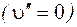 на различные колебательные уровни верхнего электронного состояния
на различные колебательные уровни верхнего электронного состояния 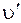 (см. рис. 1). Если величина колебательного кванта в электронном состоянии невелика или температура достаточно высока, то часть молекул находится в возбужденном состоянии
(см. рис. 1). Если величина колебательного кванта в электронном состоянии невелика или температура достаточно высока, то часть молекул находится в возбужденном состоянии 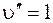 , и поэтому при поглощении могут возникнуть переходы и из первого возбужденного колебательного состояния.
, и поэтому при поглощении могут возникнуть переходы и из первого возбужденного колебательного состояния.
При интерпретации экспериментальных спектров сведения о структуре электронно-колебательной полосы молекулы сводятся в таблицу, называемую схемой Деландра. Она имеет вид таблицы, в которую занесены значения частот (волновых чисел) электронно-колебательных компонент полосы.
 |
Определив экспериментально частоты (волновые числа ) электронно-колебательных переходов в спектре поглощения и отнеся их к поперечной серии в схеме Деландра при 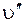 = 0, можно, пользуясь формулой (6), определить характеристики молекулы
= 0, можно, пользуясь формулой (6), определить характеристики молекулы 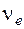 , а также
, а также 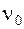 ,
, 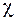 ,
, 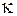 молекулы в возбужденном электронном состоянии
молекулы в возбужденном электронном состоянии 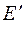 . Кроме того можно вычислить энергию диссоциации
. Кроме того можно вычислить энергию диссоциации 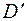 молекулы в верхнем состоянии, т.е. найти максимальную колебательную энергию молекулы в данном состоянии.
молекулы в верхнем состоянии, т.е. найти максимальную колебательную энергию молекулы в данном состоянии.
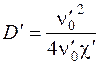 . (7)
. (7)
 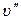 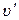 | …. | |||||
| …. |
