Потери при экспоненциальном спадании поляризации со временем
Примем, что все молекулы имеют одно и то же время жизни τж и что после выключения электрического поля поляризация убывает по экспоненциальному закону со временем релаксации
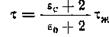
здесь множитель перед τж обусловлен, как уже отмечалось, предположением, что локальное поле равно полю Лорентца. Пренебрегая сквозной проводимостью, выпишем и проанализируем формулы для ε', ε" и tg δ:
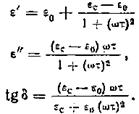
Время релаксации τ зависит от среднего времени оседлой жизни молекулы τж, которое в свою очередь зависит от температуры. При заданной температуре величина τ постоянна. Рассмотрим частотные зависимости ε', ε" и tg δ при постоянной температуре.
В частотном ходе ε" имеется максимум на частоте ωm, определяемой соотношением
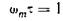 ,
,
которое можно получить, взяв производную от ε" по ωτ и приравняв ее нулю. В максимуме величина ε" равна ε"max,
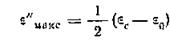 .
.
В точке максимума ε" вещественная часть диэлектрической проницаемости имеет величину
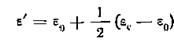 .
.
Беря производную от tg δ по ωτ и приравнивая ее нулю, с учетом находим, что tg δ проходит через максимум при частоте ω0, более высокой, чем ωm, которая определяется из ,
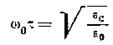 .
.
Величина tg δ в максимуме достигает значения
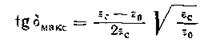 .
.
Сопоставляя выражения и , видим, что величина tgδmax в 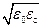 раз меньше, чем ε"max. Зависимость ε', ε" и tg δ от частоты показана на Рис. 7‑3.
раз меньше, чем ε"max. Зависимость ε', ε" и tg δ от частоты показана на Рис. 7‑3.
При повышении температуры величина τж уменьшается, вследствие чего уменьшается и время релаксации поляризации τ. Это вызывает смещение максимумов ε" и tg δ в сторону высоких частот при повышении температуры. Температурные зависимости tgδ при двух различных температурах T1 и T2 (причем T1 < T2) показаны на Рис. 7‑4.
Величина ε" и tg δ в максимуме не зависит от температуры, если при повышении температуры величины εс и ε0 не изменяются. Если же εс возрастает с увеличением температуры, то, согласно , и , ε"max и tgδmax при повышении температуры увеличиваются, причем максимум tgδ сдвигается в сторону высоких частот более быстро, чем в том случае, когда εс не зависит от температуры.
На Рис. 7‑4, б приведены температурные зависимости tg δ с учетом потерь сквозной проводимости, которая увеличивается с повышением температуры и обусловливает увеличение tg δ при уменьшении частоты в области низких частот.
В общем формулы можно применять в случае диэлектриков с любым видом релаксационной поляризации, если после выключения электрического поля поляризация убывает по экспоненциальному закону. В частности, эти формулы одинаково хороши как для диэлектриков с дипольно-ориентационной, так и для диэлектриков с ионно-релаксационной поляризацией.
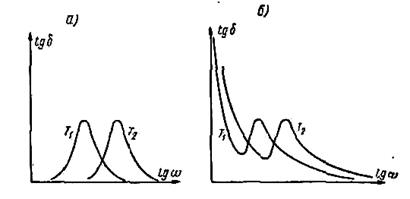 Рис. 7‑4. Частотная зависимость tg δ при температурах T1 и T2 (T1 < T2): а — без учета потерь сквозной проводимости; б — с учетом потерь сквозной проводимости Рис. 7‑4. Частотная зависимость tg δ при температурах T1 и T2 (T1 < T2): а — без учета потерь сквозной проводимости; б — с учетом потерь сквозной проводимости |
