Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает

Существует два классических определения второго закона термодинамики :

• Кельвина и Планка

Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

• Клаузиуса

Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Второй закон связан с понятием энтропии (S).

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

• 100% энергии не может быть преобразовано в работу
• Энтропия может вырабатываться, но не может быть уничтожена

Эффективность теплового двигателя

Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры

η = ( T_h - T_c ) / T_h = 1 - T_c / T_h

где

η = эффективность

T_h = верхняя граница температуры (K)

T_c = нижняя граница температуры (K)

Для того, чтобы достичь максимальной эффективности T_c должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, T_c должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).

• Изменение энтропии > 0
  Необратимыйпроцесс
• Изменение энтропии= 0
  Двустороннийпроцесс (обратимый)
• Изменение энтропии < 0
  Невозможный процесс (неосуществимый)

Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.

Определение энтропии

Энтропия определяется как :

S = H / T

где

S = энтропия (кДж/кг*К)

H = энтальпия (кДж/кг)

T = абсолютная температура (K)

Изменение энтропии системы вызвано изменением содержания темпла в ней. Изменение энтропии равно изменению темпла системы деленной на среднюю абсолютную температуру ( T_a):

dS = dH / T_a

Сумма значений (H / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.

№16
Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
Для одного моля газа Ван-дер-Ваальса оно имеет вид:

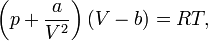
где

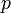• — давление,
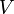• — молярный объём,
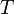• — абсолютная температура,
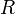• — универсальная газовая постоянная.

№17
Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

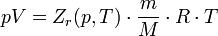
где p — давление; V - объем T — температура; Z_r = Z_r (p,T) — коэффициент сжимаемости газа; m - масса; М —молярная масса; R — газовая постоянная.

№18
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Площадь поверхности

С поверхностью жидкости связана свободная энергия

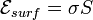
где 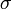— коэффициент поверхностного натяжения, 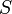— полная площадь поверхности жидкости^[4]. Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля принимает форму шара, однако при более сложных условиях задача о форме поверхности жидкости становится исключительно сложной.

[править]Формула Лапласа

Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется существование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давленияплёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и даётся формулой Лапласа:

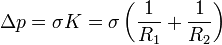
Капиллярные явления, поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее поверхности. Искривление поверхности жидкости на границе с газовой фазой происходит в результате действияповерхностного натяжения жидкости, которое стремится сократить поверхность раздела и придать ограниченному объему жидкости форму шара. Поскольку шар обладает минимальной поверхностью при данном объеме, такая форма отвечает минимуму поверхностной энергии жидкости, т.е. ее устойчивому равновесному состоянию. В случае достаточно больших масс жидкости действие поверхностного натяжения компенсируется силой тяжести, поэтому маловязкая жидкость быстро принимает форму сосуда, в который она налита, а ее своб. поверхность представляется практически плоской.

В отсутствие силы тяжести или в случае очень малых масс жидкость всегда принимает сферическую форму (капля), кривизна поверхности которой определяет мн. свойства вещества. Поэтому капиллярные явления ярко выражены и играют существенную роль в условиях невесомости, при дроблении жидкости в газовой среде (или распылении газа в жидкости) и образовании систем, состоящих из многих капель или пузырьков (эмульсий, аэрозолей,пен), призарождении новой фазы капель жидкости при конденсации паров. пузырьков пара при вскипании, зародышейкристаллизации. При контакте жидкости с конденсированными телами (другой жидкостью или твердым телом) искривление поверхности раздела происходит в результате действия межфазного натяжения.

В случае смачивания, например, при соприкосновении жидкости с твердой стенкой сосуда, силы притяжения, действующие между молекулами твердого тела и жидкости, заставляют ее подниматься по стенке сосуда, вследствие чего примыкающий к стенке участок поверхности жидкости принимает вогнутую форму. В узких каналах, например, цилиндрических капиллярах, образуется вогнутый мениск - полностью искривленная поверхность жидкости