Электромагнитные колебания и волны
Пример решения задач
36. В колебательном контуре амплитуда колебаний напряжения на обкладках конденсатора за время 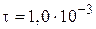 с уменьшается в
с уменьшается в 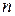 раз (
раз ( 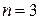 ). Найти: а) величину коэффициента затухания
). Найти: а) величину коэффициента затухания 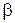 контура; б) величину активного сопротивления
контура; б) величину активного сопротивления 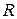 контура; в) добротность
контура; в) добротность 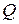 контура, если электроемкость конденсатора
контура, если электроемкость конденсатора 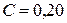 мкФ, индуктивность катушки
мкФ, индуктивность катушки 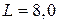 Гн.
Гн.
Дано: 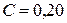 мкФ мкФ 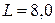 Гн Гн 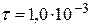 с с 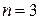 | Решение В колебательном контуре происходят затухающие электрические колебания. Амплитуда колебаний напряжения на обкладках конденсатора 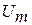 со временем со временем 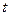 уменьшается по закону уменьшается по закону |
а) 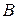 -? б) -? б) 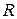 -7 в) -7 в) 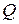 -? -? | 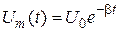 , (1) где , (1) где 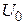 – постоянная величина. – постоянная величина. |
Через промежуток времени 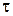 амплитуда напряжения
амплитуда напряжения
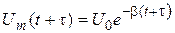 (2)
(2)
и уменьшается в 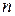 раз. Поэтому из выражений (1) и (2) получается
раз. Поэтому из выражений (1) и (2) получается
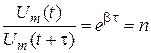 . (3)
. (3)
Прологарифмировав выражение (3), для коэффициента затухания имеем 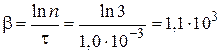 с-1.
с-1.
Коэффициент затухания 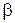 и активное сопротивление
и активное сопротивление 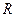 контура связаны соотношением:
контура связаны соотношением:
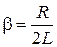 . (4)
. (4)
Отсюда для величины 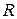 следует:
следует: 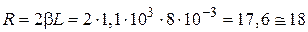 Ом.
Ом.
Как известно, добротность контура определяется формулой:
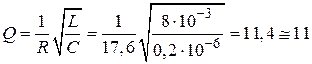
Ответ: а) 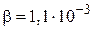 с-1; б)
с-1; б) 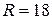 Ом; в)
Ом; в) 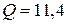
37. Цепь переменного тока частотой 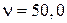 Гц и напряжения
Гц и напряжения 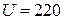 В состоит из последовательно соединенных конденсатора электроемкости
В состоит из последовательно соединенных конденсатора электроемкости 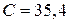 мкФ, катушки индуктивности
мкФ, катушки индуктивности 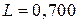 Гн, активного сопротивления
Гн, активного сопротивления 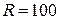 Ом. Найти: а) импеданс (полное сопротивление)
Ом. Найти: а) импеданс (полное сопротивление) 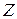 ; б) сдвиг по фазе
; б) сдвиг по фазе 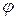 между током и напряжением; в) силу тока
между током и напряжением; в) силу тока 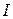 ; г) падение напряжения на конденсаторе
; г) падение напряжения на конденсаторе 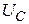 , катушке
, катушке 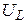 , активном сопротивлении
, активном сопротивлении 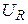 .
.
Дано: 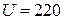 В В 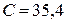 мкФ мкФ 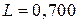 Гн Гн 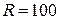 Ом Ом 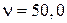 Гц Гц | Решение Величины, характеризующие протекание тока циклической частоты 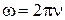 в цепи, определяется выражениями для индуктивного сопротивления в цепи, определяется выражениями для индуктивного сопротивления 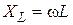 , емкостного сопротивления , емкостного сопротивления 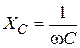 , реактивного сопротивления , реактивного сопротивления 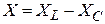 . . |
a) 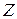 – ? б) – ? б) 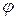 – ? в) – ? в) 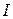 – ? г) – ? г) 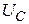 – ? – ? 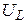 – ? – ? 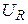 – ? – ? | Поэтому для искомых в задаче величин имеем: а) 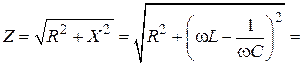 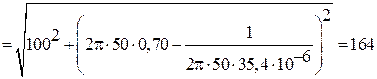 Ом. Ом. |
б) 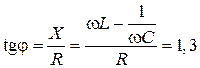 ,
, 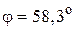 ;
;
в) 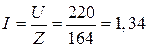 А; г)
А; г) 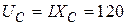 В;
В;
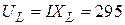 В;
В; 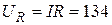 В
В
Ответ: а) 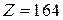 Ом; б)
Ом; б) 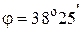 ; в)
; в) 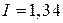 А; г)
А; г) 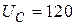 В;
В; 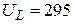 В;
В; 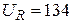 В.
В.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
4.8. Уравнение изменения силы тока в колебательном контуре дается в виде I = -0,020×sin400 pt (A). Индуктивность контура 1,0 Гн. Найти:
а) период колебаний;
б) емкость контура;
в) максимальную разность потенциалов на обкладках конденсатора.
(T = 5·10-3 c; C = 6,3·10-7 Ф; Umax = 25 B)
4.9. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре дано в виде
U = 50×сos104pt (В). Емкость конденсатора составляет 9×10-7 Ф. Найти:
а) период колебаний;
б) индуктивность контура;
в) закон изменения со временем силы тока в цепи;
г) длину волны, соответствующую этому контуру.
(T = 2·10-4 c, L = 1,1 мГн, I = -1,4×sin104×pt А, l = 6∙104 м)
4.10. Колебательный контур состоит из конденсатора ёмкостью С = 7 мкФ, катушки индуктивности L = 0,23 Гн и сопротивления R = 40 Ом. Конденсатор заряжен количеством электричества Q = 5,6×10-4 Кл. Найти:
а) период колебаний контура;
б) логарифмический декремент затухания колебаний.
Написать уравнение зависимости изменения разности потенциалов на обкладках конденсатора от времени.
(T = 8·10-3 c; l = 0,7; U = 80 exp(-87×t)cos(250 pt))
4.11. В цепь переменного тока напряжением 220 В включены последовательно емкость С, активное сопротивление R и индуктивность L. Найти падение напряжения UR на омическом сопротивлении, если известно, что падение напряжения на конденсаторе равно UC = 2UR и падение напряжения на индуктивности UL = 3UR.
(UR = 156 B)
4.12. Цепь переменного тока образована последовательно включенными активным сопротивлением R = 800 Ом, индуктивностью L = 1,27 Гн и ёмкостью С = 1,59 мкФ. На зажимы подано 50-периодное действующее напряжение U = 127 В. Найти:
а) действующее значение силы тока I в цепи;
б) сдвиг по фазе между током и напряжением;
в) действующее значение напряжений UR, UL и UC на зажимах каждого элемента цепи.
(71 мА; -63°; 57 В; 28 В; 142 В)
4.13. Колебательный контур состоит из конденсатора емкостью С = 25 нФ и катушки с индуктивностью L = 1,015 Гн. Обкладкам конденсатора сообщается заряд q = 2,5 мкКл. Написать уравнения (с числовыми коэффициентами) изменения разности потенциалов U и тока I в цепи от времени. Найти разность потенциалов на обкладках конденсатора и ток в цепи в моменты времени T/8, T/4, T/2 (T – период колебаний). Построить графики U(t) и I(t) в пределах одного периода.
( 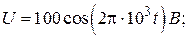
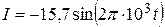 мА;
мА; 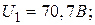
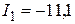 мА;
мА; 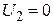 ;
; 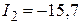 мА;
мА; 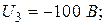
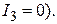
4.14. В однородной и изотропной среде с 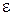 = 3,0 и
= 3,0 и 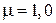 распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны
распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 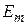 = 10,0 В/м. Найти: а) амплитуду напряженности магнитного поля волны
= 10,0 В/м. Найти: а) амплитуду напряженности магнитного поля волны 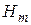 , б)фазовую скорость
, б)фазовую скорость 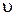 волны.
волны.
( 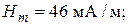
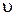 =
= 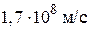 )
)
Оптика
Пример решения задач
38. На мыльную пленку с показателем преломления 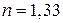 падает по нормали пучок лучей белого света. При какой наименьшей толщине пленки
падает по нормали пучок лучей белого света. При какой наименьшей толщине пленки 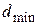 она в отраженном свете будет казаться зеленой (
она в отраженном свете будет казаться зеленой ( 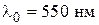 )?
)?
Дано: 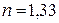 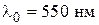 | Решение  |
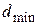 – ? – ? |
Для того, чтобы в отраженном свете пленка выглядела зеленой, необходимо, чтобы при интерференции отраженных лучей выполнялось условие максимума для зеленой части спектра. Оптическая разность хода 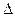 лучей 3 и 2, отраженных от нижней и верхней поверхностей пленки,
лучей 3 и 2, отраженных от нижней и верхней поверхностей пленки,
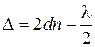 ,
,
(оптический ход в плёнке луча 3 больше луча 2 на 2dn, но луч 2 отражается от оптически более плотной среды, поэтому его ход скачком увеличивается на 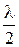 ). Условие максима:
). Условие максима:
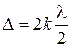 ,
,
где k = 0, 1, 2… . Наименьшая толщина пленки будет при k = 0, тогда
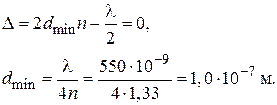
Ответ: 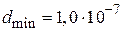 м.
м.
39. На прозрачную дифракционную решетку с периодом 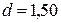 мкм падает нормально монохроматический свет с длинной волны
мкм падает нормально монохроматический свет с длинной волны 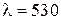 нм. Найти: а) наибольший порядок
нм. Найти: а) наибольший порядок 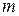 главного дифракционного максимума; б) угол дифракции
главного дифракционного максимума; б) угол дифракции 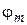 главного дифракционного максимума наибольшего порядка.
главного дифракционного максимума наибольшего порядка.
Дано: 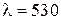 нм нм 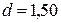 мкм мкм | Решение Условие главного дифракционного максимума порядка 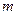 имеет вид имеет вид 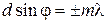 , ( , ( 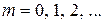 ), ), |
а) 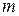 – ? б) – ? б) 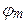 – ? – ? | где  – угол дифракции, соответствующего главного максимума – угол дифракции, соответствующего главного максимума |
Как следует из выпеприведенной формулы, наибольший порядок дифракционного максимума должен удовлетворять соотношению 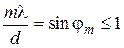 .
.
Отсюда имеем 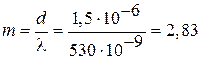 . Поскольку угол
. Поскольку угол  не может быть больше
не может быть больше 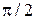 , а m должно быть целым, то выбираем m = 2. Для соответствующего угла дифракции получим
, а m должно быть целым, то выбираем m = 2. Для соответствующего угла дифракции получим 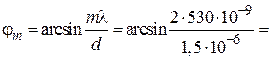 =
= 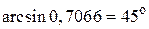
Ответ: а) 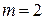 ; б)
; б) 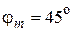
40. Луч света, падающий на поверхность кристалла каменной соли, при отражении максимально поляризуется, если угол падения 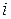 равен 57°. Найти: а) показатель преломления
равен 57°. Найти: а) показатель преломления 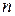 кристалла каменной соли; б) скорость распространения
кристалла каменной соли; б) скорость распространения 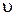 света в этом кристалле.
света в этом кристалле.
Дано: 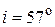 | Решение Согласно закону Брюстера отраженный луч света максимально поляризован, если угол падения луча удовлетворяет соотношению 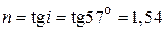 . (1) . (1) |
а) 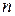 – ? б) – ? б) 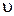 – ? – ? |
Скорость света в кристалле может быть найдена из известного соотношения:
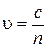 , (2)
, (2)
где 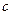 – скорость света в вакуме. Поэтому из формул (1) и (2) имеем
– скорость света в вакуме. Поэтому из формул (1) и (2) имеем
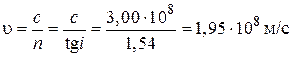 .
.
Ответ: а) 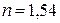 б)
б) 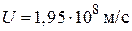
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
4.15. На мыльную пленку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волны l = 0,60 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина плёнки dmin?
(0,11 мкм)
4.16. Плоская световая волна длиной l0 в вакууме падает по нормали на прозрачную пластинку с показателем преломления n. При каких толщинах b пластинки отраженная волна будет иметь:
а) максимальную интенсивность;
б) минимальную интенсивность?
(а) b = (l0/2n)(m+0,5) (m = 1, 2, 3...); б) b = (l0/2n)m (m = 1,2,3...))
|
Красная линия (l = 6300 Å) видна в спектре 3-го порядка под углом j = 60°.
Определить:а) какая спектральная линия видна под этим же углом в спектре 4-го порядка; б) какое число штрихов на 1 мм длины имеет дифракционная решетка.
(l = 475 нм; N = 460 мм-1)
4.18. Пластина кварца толщиной d1 = 1,0 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол j1 = 20°. Определить:
а) какова должна быть длина d2 кварцевой пластинки, помещенной между двумя “параллельными” николями, чтобы свет был полностью погашен;
б) какой длины l трубку с раствором сахара концентрации С = 0,40 кг/л надо поместить между николями для получения того же эффекта.
Удельное вращение раствора сахара a0 = 0,665 град/(м-2×кг).
(d2 = 4,5 мм; l = 3,4 дм)
4.19. Под каким углом к горизонту должно находиться солнце, чтобы его лучи, отраженные от поверхности озера, стали бы наиболее полно поляризованы, если скорость света в воде 2,26×108 м/с?
(37°)
4.20. Источник света диаметром d = 30,0 см находится от места наблюдателя на расстоянии l = 200 м. В излучении источника содержатся волны длиной от 490 до 510 нм. Оценить для этого излучения: а) время когерентности 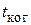 ; б) длину когерентности
; б) длину когерентности 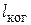 ; в) радиус когерентности
; в) радиус когерентности 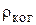 .
.
( 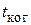
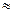
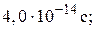
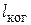
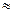 0,010 мм;
0,010 мм; 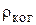
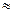 0,30 мм)
0,30 мм)
4.21. Пластинка кварца толщиной d = 4,0 мм (удельное вращение кварца 15 град/мм), вырезанная перпендикулярно оптической оси, помещена между двумя скрещенными николями. Пренебрегая потерями света в николях, определите, во сколько раз уменьшится интенсивность света, прошедшего эту систему.
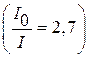 .
.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Таблица вариантов задач к разделу «Механика»
| Вариант | Номер задачи | ||||
| 1.1 | 1.16 | 1.22 | 1.44 | 1.65 | |
| 1.2 | 1.17 | 1.23 | 1.45 | 1.66 | |
| 1.3 | 1.18 | 1.25 | 1.46 | 1.67 | |
| 1.4 | 1.19 | 1.26 | 1.47 | 1.68 | |
| 1.5 | 1.20 | 1.27 | 1.48 | 1.69 | |
| 1.6 | 1.21 | 1.28 | 1.49 | 1.70 | |
| 1.7 | 1.16 | 1.29 | 1.50 | 1.71 | |
| 1.8 | 1.17 | 1.30 | 1.51 | 1.71 | |
| 1.9 | 1.18 | 1.31 | 1.52 | 1.65 | |
| 1.10 | 1.19 | 1.32 | 1.53 | 1.66 | |
| 1.11 | 1.20 | 1.33 | 1.67 | ||
| 1.12 | 1.21 | 1.34 | 1.55 | ||
| 1.16 | 1.35 | 1.56 | 1.69 | ||
| 1.14 | 1.17 | 1.36 | 1.57 | 1.70 | |
| 1.15 | 1.18 | 1.37 | 1.58 | 1.71 | |
| 1.1 | 1.19 | 1.71 | |||
| 1.2 | 1.20 | 1.39 | 1.60 | 1.65 | |
| 1.3 | 1.21 | 1.40 | 1.61 | 1.66 | |
| 1.16 | 1.41 | 1.62 | |||
| 1.5 | 1.17 | 1.42 | 1.63 | 1.68 | |
| 1.6 | 1.18 | 1.43 | 1.69 | ||
| 1.7 | 1.19 | 1.22 | 1.45 | 1.70 | |
| 1.8 | 1.20 | 1.23 | 1.46 | 1.71 | |
| 1.9 | 1.21 | 1.25 | 1.47 | 1.71 | |
| 1.10 | 1.16 | 1.26 | 1.48 | 1.65 | |
| 1.11 | 1.17 | 1.27 | 1.49 | 1.66 | |
| 1.12 | 1.18 | 1.28 | 1.50 | 1.67 | |
| 1.13 | 1.19 | 1.29 | 1.51 | 1.68 | |
| 1.14 | 1.20 | 1.30 | 1.52 | 1.69 | |
| 1.15 | 1.21 | 1.31 | 1.53 | 1.70 |
Таблица вариантов задач к разделу
«Молекулярная физика и термодинамика»
| Вариант | Номер задачи | ||||
| 2.1 | 2.6 | 2.12 | 2.20 | 2.33 | |
| 2.2 | 2.7 | 2.13 | 2.21 | 2.34 | |
| 2.3 | 2.8 | 2.14 | 2.22 | 2.35 | |
| 2.4 | 2.9 | 2.15 | 2.23 | 2.36 | |
| 2.5 | 2.10 | 2.16 | 2.24 | 2.37 | |
| 2.1 | 2.11 | 2.17 | 2.25 | 2.33 | |
| 2.2 | 2.6 | 2.18 | 2.26 | 2.34 | |
| 2.3 | 2.7 | 2.19 | 2.27 | 2.35 | |
| 2.4 | 2.8 | 2.12 | 2.28 | 2.36 | |
| 2.5 | 2.9 | 2.13 | 2.29 | 2.37 | |
| 2.1 | 2.10 | 2.14 | 2.30 | 2.33 | |
| 2.2 | 2.11 | 2.15 | 2.31 | 2.34 | |
| 2.3 | 2.6 | 2.16 | 2.32 | 2.35 | |
| 2.4 | 2.7 | 2.17 | 2.20 | 2.36 | |
| 2.5 | 2.8 | 2.18 | 2.21 | 2.37 | |
| 2.1 | 2.9 | 2.19 | 2.22 | 2.33 | |
| 2.2 | 2.10 | 2.12 | 2.23 | 2.34 | |
| 2.3 | 2.11 | 2.13 | 2.24 | 2.35 | |
| 2.4 | 2.6 | 2.14 | 2.25 | 2.36 | |
| 2.5 | 2.7 | 2.15 | 2.26 | 2.37 | |
| 2.1 | 2.8 | 2.16 | 2.27 | 2.33 | |
| 2.2 | 2.9 | 2.17 | 2.28 | 2.34 | |
| 2.3 | 2.10 | 2.18 | 2.29 | 2.35 | |
| 2.4 | 2.11 | 2.19 | 2.30 | 2.36 | |
| 2.5 | 2.6 | 2.12 | 2.31 | 2.37 | |
| 2.1 | 2.7 | 2.13 | 2.32 | 2.33 | |
| 2.2 | 2.8 | 2.14 | 2.20 | 2.34 | |
| 2.3 | 2.9 | 2.15 | 2.21 | 2.35 | |
| 2.4 | 2.10 | 2.16 | 2.22 | 2.36 | |
| 2.5 | 2.11 | 2.17 | 2.23 | 2.37 |
Таблица вариантов задач к разделу
«Электричество и магнетизм»
| Вариант | Номер задачи | ||||
| 3.1 | 3.10 | 3.16 | 3.23 | 3.33 | |
| 3.2 | 3.11 | 3.17 | 3.24 | 3.34 | |
| 3.3 | 3.12 | 3.18 | 3.25 | 3.35 | |
| 3.4 | 3.13 | 3.19 | 3.26 | 3.36 | |
| 3.5 | 3.14 | 3.20 | 3.27 | 3.33 | |
| 3.6 | 3.15 | 3.21 | 3.28 | 3.34 | |
| 3.7 | 3.10 | 3.22 | 3.29 | 3.35 | |
| 3.8 | 3.11 | 3.16 | 3.30 | 3.36 | |
| 3.9 | 3.12 | 3.17 | 3.31 | 3.37 | |
| 3.1 | 3.13 | 3.18 | 3.32 | 3.38 | |
| 3.2 | 3.14 | 3.19 | 3.23 | 3.39 | |
| 3.3 | 3.15 | 3.20 | 3.24 | 3.40 | |
| 3.4 | 3.10 | 3.21 | 3.25 | 3.33 | |
| 3.5 | 3.11 | 3.22 | 3.26 | 3.34 | |
| 3.6 | 3.12 | 3.16 | 3.27 | 3.35 | |
| 3.7 | 3.13 | 3.17 | 3.28 | 3.36 | |
| 3.8 | 3.14 | 3.18 | 3.29 | 3.37 | |
| 3.9 | 3.15 | 3.19 | 3.30 | 3.38 | |
| 3.1 | 3.10 | 3.20 | 3.31 | 3.39 | |
| 3.2 | 3.11 | 3.21 | 3.32 | 3.40 | |
| 3.3 | 3.12 | 3.22 | 3.23 | 3.33 | |
| 3.4 | 3.13 | 3.16 | 3.24 | 3.34 | |
| 3.5 | 3.14 | 3.17 | 3.25 | 3.35 | |
| 3.6 | 3.15 | 3.18 | 3.26 | 3.36 | |
| 3.7 | 3.10 | 3.19 | 3.27 | 3.37 | |
| 3.8 | 3.11 | 3.20 | 3.28 | 3.38 | |
| 3.9 | 3.12 | 3.21 | 3.29 | 3.39 | |
| 3.1 | 3.13 | 3.22 | 3.30 | 3.40 | |
| 3.2 | 3.14 | 3.16 | 3.31 | 3.37 | |
| 3.3 | 3.15 | 3.17 | 3.32 | 3.39 |
Таблица вариантов задач к разделу «Колебания, волны, оптика»
| Вариант | Номер задачи | |||
| 4.1 | 4.7 | 4.8 | 4.15 | |
| 4.2 | 4.6 | 4.9 | 4.16 | |
| 4.3 | 4.5 | 4.9 | 4.17 | |
| 4.4 | 4.5 | 4.10 | 4.18 | |
| 4.1 | 4.6 | 4.11 | 4.19 | |
| 4.2 | 4.7 | 4.12 | 4.20 | |
| 4.3 | 4.5 | 4.13 | 4.21 | |
| 4.4 | 4.6 | 4.14 | 4.17 | |
| 4.1 | 4.7 | 4.8 | 4.18 | |
| 4.2 | 4.5 | 4.9 | 4.19 | |
| 4.3 | 4.6 | 4.9 | 4.20 | |
| 4.4 | 4.7 | 4.10 | 4.16 | |
| 4.1 | 4.5 | 4.11 | 4.17 | |
| 4.2 | 4.6 | 4.13 | 4.18 | |
| 4.3 | 4.6 | 4.14 | 4.19 | |
| 4.4 | 4.5 | 4.14 | 4.15 | |
| 4.1 | 4.6 | 4.8 | 4.21 | |
| 4.2 | 4.7 | 4.9 | 4.17 | |
| 4.3 | 4.5 | 4.9 | 4.18 | |
| 4.4 | 4.6 | 4.8 | 4.19 | |
| 4.1 | 4.7 | 4.10 | 4.15 | |
| 4.2 | 4.5 | 4.11 | 4.16 | |
| 4.3 | 4.6 | 4.12 | 4.17 | |
| 4.4 | 4.5 | 4.13 | 4.18 | |
| 4.1 | 4.5 | 4.14 | 4.19 | |
| 4.2 | 4.6 | 4.9 | 4.20 | |
| 4.3 | 4.6 | 4.9 | 4.21 | |
| 4.4 | 4.5 | 4.8 | 4.17 | |
| 4.1 | 4.6 | 4.10 | 4.18 | |
| 4.2 | 4.7 | 4.11 | 4.19 |
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ*
1. Кунин, В. Н. Программа по физике / В. Н. Кунин, К. И. Пак ; Владим. гос. техн. ун-т. – Владимир : 1992. – 32 с.
2. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М. : Наука, 1987. – 607 с.
3. Савельев, И. В. Курс общей физики. В 3 т. Т. 1 / И. В. Савельев. – М. : Наука, 1987. – 432 с.
4. Он же. Курс общей физики. В 3 т. Т. 2 / И. В. Савельев. – М. : Наука,1988. – 496 с.
5. Трофимова, Т. И. Курс физики / Т. И. Трофимова. – М. : Высш. шк., 1990. – 478 с.
6. Сивухин, Д. В. Общий курс физики. В 5 т. Т. 1 / Д. В. Сивухин. – М. : Наука, 1974. – 519 с.
7. Он же. Общий курс физики. В 5 т. Т. 2 / Д. В. Сивухин. – М. : Наука, 1975. – 551 с.
8. Он же. Общий курс физики. В 5 т. Т. 3 / Д. В. Сивухин. – М. : Наука, 1977. – 687 с.
9. Он же. Общий курс физики. В 5 т. Т. 4 / Д. В. Сивухин. – М. : Наука, 1980. – 751 с.
10. Калашников, Э. Г. Электричество / Э. Г. Калашников. – М. : Наука, 1997. – 590 с.
11. Ландсберг, Г. С. Оптика / Г. С. Ландсберг. – М. : Наука, 1976. – 926 с.
12. Волькенштейн, В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. – М. : Наука, 1979. – 351 с.
13. Савельев, И. В. Сборник вопросов и задач по общей физике / И. В. Савельев. – М. : Наука, 1988. – 288 с.
14. Иродов, И. Е. Сборник задач по общей физике / И. Е. Иродов, И. В. Савельев, О. И. Замша. – М. : Наука, 1975. – 319 с.
15. Физика : программа, методические указания и задачи для студентов-заочников (с примерами решения) ; Владим. гос. ун-т. ; сост. : А. Ф. Галкин [и др.] ; под ред. А. А. Кулиша. – Владимир, 2002. – 128 с.
16. Трофимова, Т. П. Сборник задач по курсу физики с решениями / Т. П. Трофимова, З. Г. Павлова. – М. : Высш. шк., 1999. – 591 с.
17. Стрелков, С. П. Механика / С. П. Стрелков. – М. : Наука, 1975. – 559 с.
18. Годжаев, Н. М. Оптика / Н. М. Годжаев. – М. : Высш. шк., 1977. – 432 с.
ОГЛАВЛЕНИЕ
Цели и задачи курса физики, его место в учебном процессе...... 3
Общие методические указания .................................................... 5
Программа.................................................................................... 7
Вопросы, входящие в экзаменационые билеты......................... 15
Темы практических занятий ...................................................... 21
Список лабораторных работ...................................................... 22
Примерные темы курсовых работ............................................. 24
Программа коллоквиумов.......................................................... 25
Зачетные требования................................................................... 26
Вопросы и задачи по физике с примерами решения................. 29
Контрольные задания................................................................. 39
Список рекомендуемой литературы........................................ 124
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, ПРОГРАММА,
ВОПРОСЫ И ЗАДАЧАМИ ПО ФИЗИКЕ
Составили
КУНИН Владимир Николаевич
ГАЛКИН Аркадия Федорович
Подписано в печать 09.02.07.
Формат 60х84/16. Усл. печ. л. ?,??. Тираж ?00 экз.
Заказ
Издательство
Владимирского государственного университета.
 600000, Владимир, ул. Горького, 87.
600000, Владимир, ул. Горького, 87.
* В скобках указаны номера лабораторных работ.
* Можно использовать издания более поздних годов выпуска.
