Электропроводность металлов

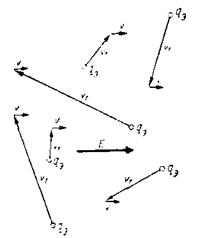Рис. 5‑1 Составляющие скорости v электронов в направлении напряженности поля vT - тепловая скорость

Для металлов характерна электронная электропроводность, при которой (в отличие от ионной и молионной электропроводности) отсутствует «видимый» перенос вещества при прохождении через вещество электрического тока.

Проводимость при нормальных условиях. Когда на металл не действует внешнее электрическое поле, распределение скоростей v_T «теплового» движения электронов, которыми определяется проводимость металла, по различным направлениям равновероятно, почему геометрическая сумма этих скоростей для некоторого, достаточно большого, объема металла в любой момент равна нулю. Поэтому в отсутствие приложенного извне напряжения ток через металл не протекает.

Если же к металлу приложено напряжение, так что в металле создается электрическое поле с напряженностью Е (Рис. 5‑1), то на каждый электрон будет действовать дополнительная механическая сила

,

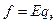где q_э — зарядэлектрона.

Электрон с массой m приобретает постоянное ускорение в направлении Е, равное

.

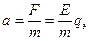Через время t с момента начала движения обусловленная электрическим полем составляющая скорости электрона достигнет величины

.

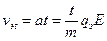Скорость электрона v_э под действием электрического поля не может возрастать безгранично, так как электроны испытывают рассеяния на узлах решетки; после каждого столкновения скорость электрона падает до нуля, а затем опять увеличивается, имея постоянное ускорение. Таким образом, составляющая скорости v_э какого-либо индивидуально рассматриваемого электрона должна изменяться в функции времени t согласно пилообразному графику, приведенному на Рис. 5‑2. Наибольшее значение составляющей скорости v_э данного электрона в конце каждого периода ускорения продолжительностью τ (время свободногопробега электрона), равно

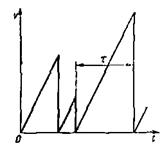Рис. 5‑2 Скачкообразные изменения скорости v носителя заряда со временем

,

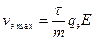а средняя скорость его за время τ

.

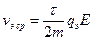Найдем среднее значение τ_ср для всех электронов, исходя из того,что согласно электронной теории метал лов «тепловая» скорость v_T значительно больше составляющей v_э, т.е. 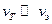; тогда

,

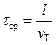где l — средняя длина свободного пробега электрона.

Если подставить в уравнение , то полученное выражение будет определять среднее значение скорости электронов в любой момент времени

.

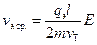Удельная объемная проводимость для металла выразите формулой , в которую вместо q надлежит подставить заряд электрона q_э, а вместо v_э его выражение из формулы . Произведя подстановки и сократив E, получим

.

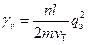Таким образом, удельная объемная электропроводность пропорциональна концентрации электронов и длине их свободного пробега. Отметим, что электропроводность не зависит от напряженности электрического поля Е.