Гармонические колебания

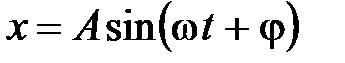– уравнение гармонических колебания переменной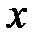

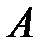– амплитуда колебаний;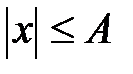

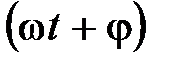– фаза.

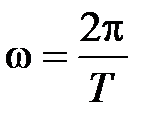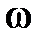; – циклическая (круговая) частота колебаний; 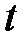– время.

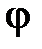– начальная фаза колебаний, 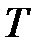– период колебаний.

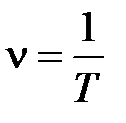– частота (линейная) колебаний.

Период колебаний математического маятника 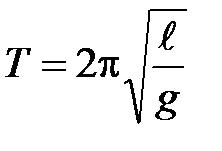; 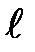– длина маятника, 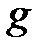– ускорение силы тяжести.

Период колебаний физического маятника ,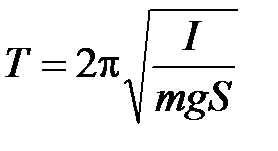

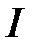– момент инерции тела относительно оси колебаний; 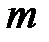– масса тела; S – расстояние от точки подвеса до центра масс.

Период колебаний пружинного маятника 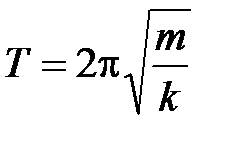, 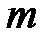– масса тела, 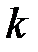– жесткость пружины.

Энергия гармонического колебания

.

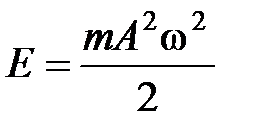Уравнение плоской монохроматической волны

,

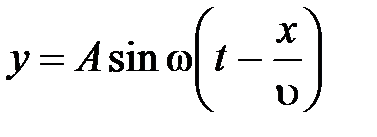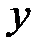– колеблющаяся величина, 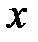– координата точки, в которой фиксируется колебание, относительно источника колебаний: 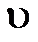– скорость распространения волны 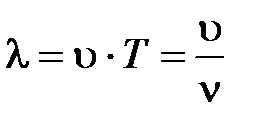– длина волны.

Затухающие колебания

Если обозначить через 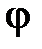колеблющуюся величину (смещение, угол, сила тока, напряжение и т.д.), то ее изменение в режиме затухания представится уравнением 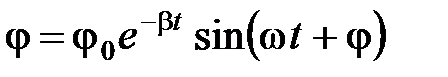; 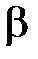– коэффициент затухания.

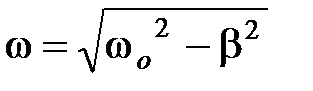– циклическая частота затухающих колебаний.

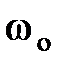– частота собственных (незатухающих) колебаний.

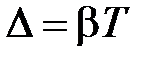– логарифмический декремент затухания.

Электромагнитные колебания

Колебания электрического заряда могут быть выражены уравнением:

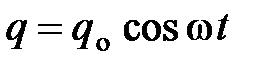
Колебания тока:

.

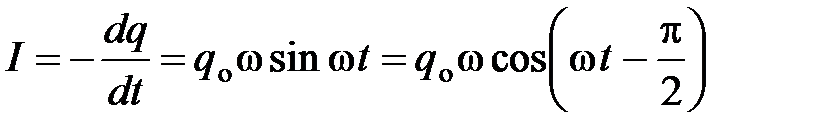Амплитудное значение тока .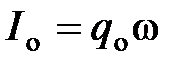

Циклическая частота колебаний 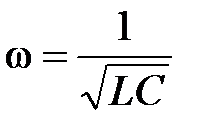; 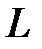– индуктивность контура, – емкость контура.

Период колебаний .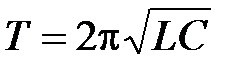

Энергия поля в контуре:

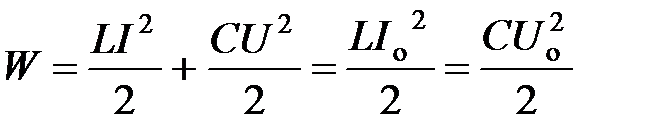, где

.

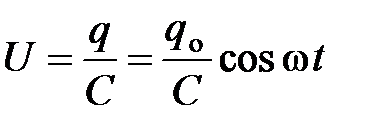Затухающие колебания

:

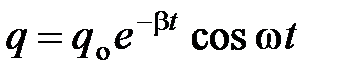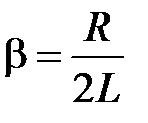– коэффициент затухания, 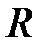– омическое сопротивление контура, 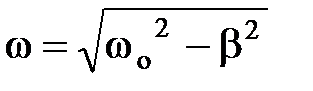– циклическая частота затухающих колебаний.

В этом выражении 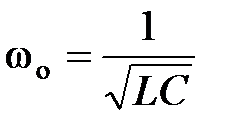– циклическая частота незатухающих колебаний.

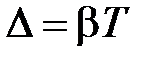– логарифмический декремент колебаний.

Вынужденные колебания

Если колебания вынуждающей ЭДС представить в виде 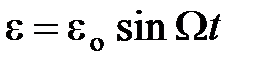, а колебания тока в контуре – 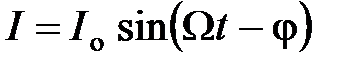, то амплитуда тока

,

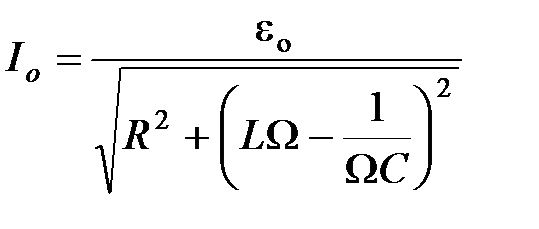сдвиг по фазе между током и вынуждающей ЭДС определяется выражением

.

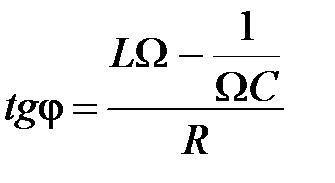Величина 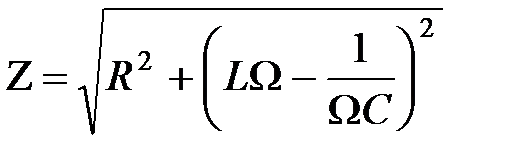– полное сопротивление цепи переменного тока (импеданс).

При 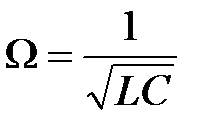имеем резонанс и при этом .

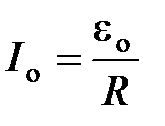Электромагнитные волны

Уравнение плоской монохроматической электромагнитной волны, распространяющейся вдоль оси :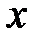

,

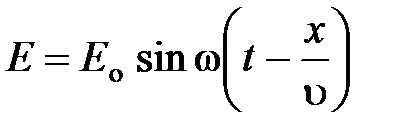
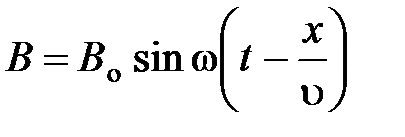где 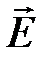– вектор электрической напряженности поля волны, 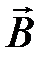– вектор магнитной индукции.

В вакууме 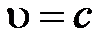(скорости света в вакууме): 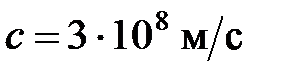относится к фундаментальным физическим постоянным.

Инварианты поля волны:

; ;

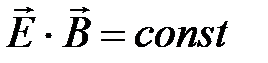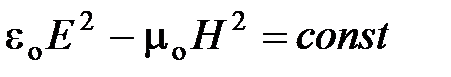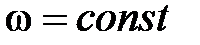
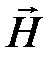( – вектор напряженности магнитного поля).

8. ОПТИКА

Основные формулы.

Лучевая оптика.

Основные законы:

1. Закон прямолинейности распространения световых лучей: световой луч в вакууме или однородной среде распространяется прямолинейно.

2. Законы отражения:

а) луч падающий, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости;

б) угол падения луча равен углу отражения.

3. Законы преломления:

а) луч падающий, луч преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости;

б) отношение синуса угла падения α к синусу угла преломления β есть величина постоянная для двух данных сред, называемая относительным показателем преломления второй среды относительно первой:

.

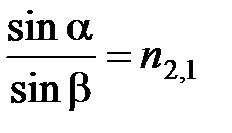В случае, если первой средой является вакуум, то показатель преломления второй среды называют абсолютным.

4. Принцип независимости световых пучков: световые пучки при пересечении не возмущают друг друга.

5. Принцип обратимости световых лучей: при обращении светового луча он пойдет тем же самым путем, по которому пришел в данную точку.

6. Принцип Ферма определяет наиболее общие геометрические свойства световых пучков: световой луч распространяется таким образом, что его оптический путь, равный 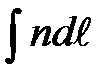принимает экстремальное значение, т.е. является или минимальным, или максимальным, или стационарным.

Преломление света

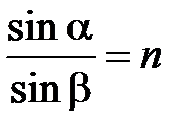, первая среда вакуум

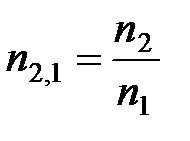– относительный показатель преломления.

Если 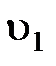– скорость распространения света в первой среде, а 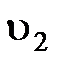– во второй среде, то .

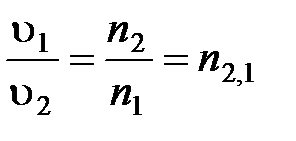Длина волны 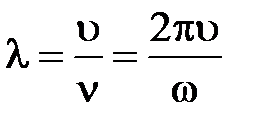, – инвариантная характеристика луча, циклическая частота его волны.

Преломление и отражение световых лучей

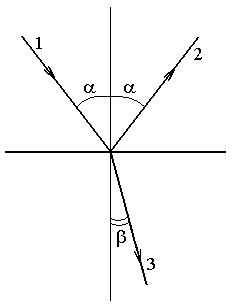1 – луч падающий на границу

раздела двух сред

2 – луч отражённый

3 – луч преломлённый

Формула тонкой собирающей линзы:

,

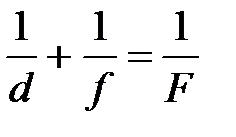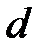– расстояние от предмета до линзы, 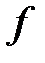– расстояние от линзы до изображения, 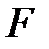– фокусное расстояние.

Формула рассеивающей линзы:

.

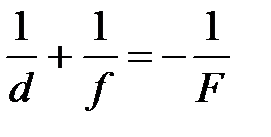Обобщенная формула тонкой линзы:

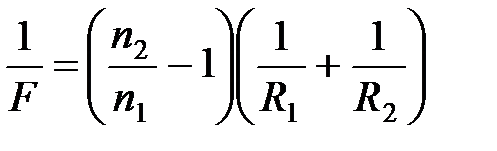
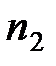– показатель преломления вещества линзы;

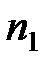– показатель преломления среды

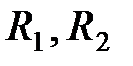– радиусы кривизны поверхностей, ограничивающих линзу.

Поперечное увеличение линзы .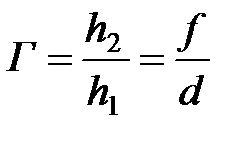

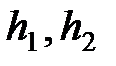– поперечные размеры изображения и предмета.

Оптическая сила системы двух линз:

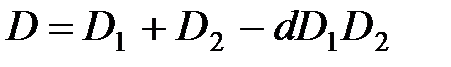
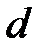– расстояние между линзами.

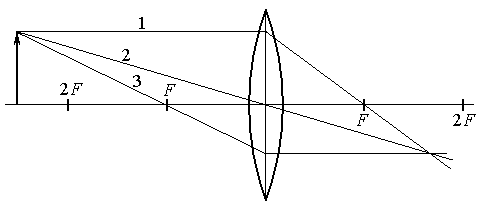
Построение изображения в тонкой линзе

Для построения изображения можно воспользоваться любой комбинацией лучей 1, 2, 3.

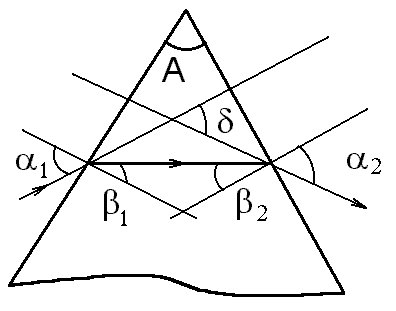
Формула призмы

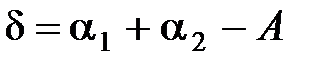
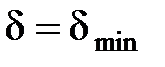при 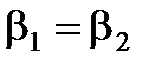и если 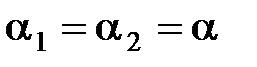, то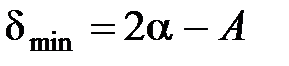

α₁ – угол падения луча на грань призмы, α₂ – угол выхода луча из призмы, A – преломляющий угол, δ – угол отклонения луча призмой.

Показатель преломления вещества призмы относительно окружающей среды

.

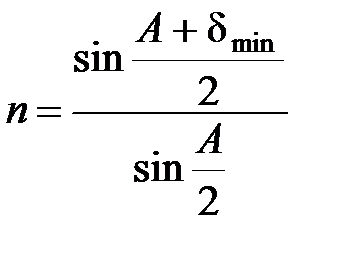Интерференция света

Условие максимума интерференции – равенство оптической разности хода лучей четному числу полуволн 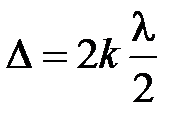, 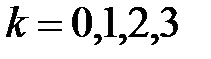– порядок максимума.

Условие минимума интерференции 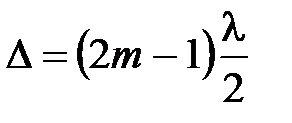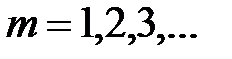.– порядок минимума.

Число различимых полос интерференции при излучении источником колебания интервала длин волн .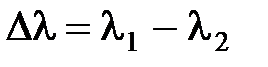

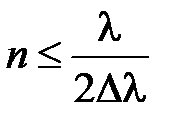, где .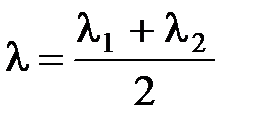

Полосы равного наклона

.

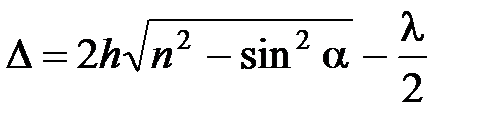При 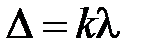; 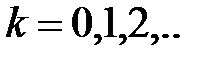– максимум интерференции в отраженном свете

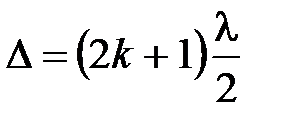минимум интерференции в отраженном свете.

Радиусы темных колец Ньютона в отраженном свете ,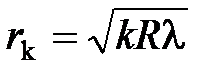

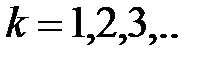
R – радиус кривизны линзы;

радиусы светлых колец

.

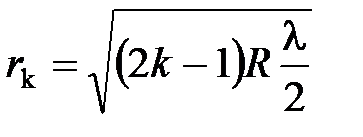Дифракция света

Дифракция Френеля

Площадь зоны Френеля для дифракции на круглом отверстии

,

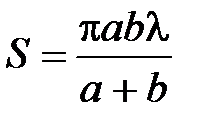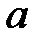– расстояние от источника света до фронта волны, 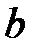– расстояние от вершины волнового фронта до точки наблюдения, 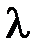– длина волны.

Радиус внешней границы 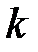-й зоны Френеля

.

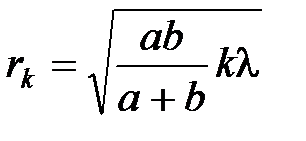Число отрытых зон Френеля

.

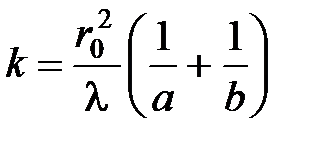Дифракционная решетка

Условие 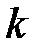-го главного максимума интенсивности: 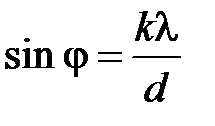, 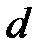– период решетки.

Условие главного минимума:

,

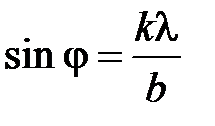где b – ширина щели в решетке.

Условие добавочных минимумов

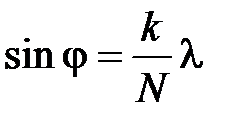, гд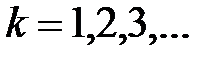е кроме .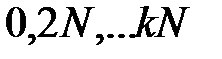

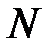– число щелей решетки.

Разрешающая способность дифракционной решетки: .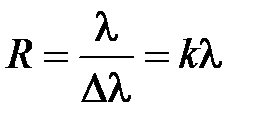

Угловое расстояние между двумя точками, разрешаемыми телескопом

,

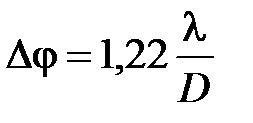D – диаметр объектива.

Поляризация света

Закон Малюса: 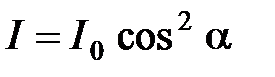, где 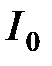– интенсивность света, входящего в анализатор; 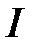– интенсивность света, выходящего из анализатора; 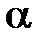– угол между плоскостями поляризации света входящего в анализатор и выходящего из анализатора.

Условие Брюстера: 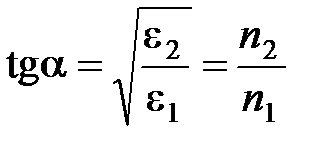, где 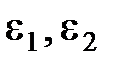– диэлектрические проницаемости сред.

Угол поворота плоскости поляризации света в оптически активных кристаллах 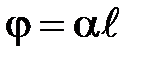, 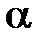– удельное вращение, зависящее от природы вещества, температуры и длины волны света (в вакууме), 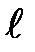– путь света в кристалле.

Угол поворота плоскости поляризации в растворах:

,

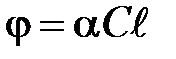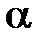– удельное вращение, зависящее от природы оптически активного вещества и растворителя, 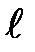– толщина слоя раствора, – концентрация оптически активного вещества.

Степень поляризации:

,

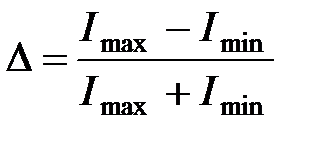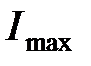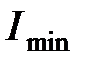где и – максимальная и минимальная интенсивность в двух взаимно перпендикулярных направлениях.

Дисперсия света.

Скорость света в изотропной прозрачной среде ; –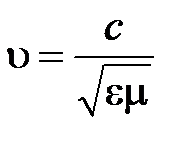

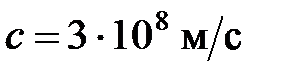скорость света в вакууме; 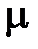– магнитная проницаемость среды, как правило 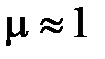; 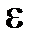– диэлектрическая проницаемость (в переменном поле) 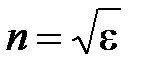и .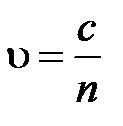

В области нормальной дисперсии зависимость 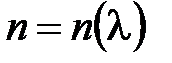выражается формулой Коши:

,

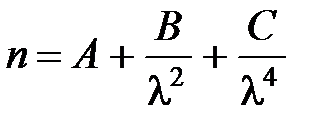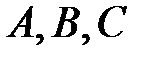– постоянные, определяемые ответным путем.

Угловая дисперсия призмы:

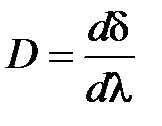, а также

.

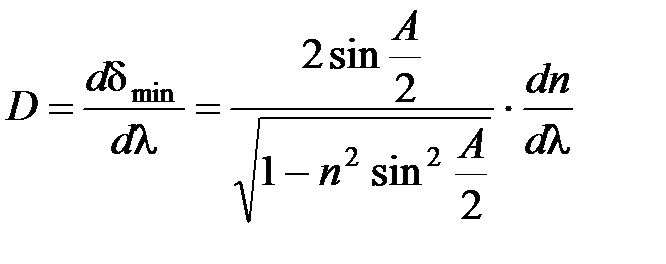Разрешающая сила призмы:

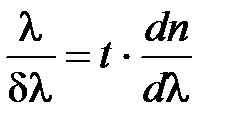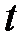; – ширина основания.