ЛАБОРАТОРНАЯ РАБОТА №18
ОПРЕДЕЛЕНИЕ ТОЧКИ КЮРИ ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ
Выполнил студент -------------------------, группа -------------, дата -------.
Допуск ______________
Выполнение __________
Зачет ________________
Цель работы: изучение температурной кривой вблизи точки Кюри для характеристики магнитных свойств ферромагнетиков.
Приборы и материалы
| № п\п | Наименование прибора | Класс точности 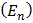 | Цена деления | Предел измерения 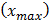 | Точность отсчета 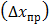 |
| Трансформатор с ферромагниным сердечником | – | – | – | – | |
| Нагреватель | – | – | – | – | |
| Датчик температуры (термопара с милливольтметром) | – | ||||
| Микроамперметр |
Теоретические сведения
Основные понятия и законы
1.1. Понятие о магнитном поле и его некоторые характеристики
Магнитное поле – одна из форм электромагнитного поля, релятивистский эффект электрического поля.
Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем (током смещения), или собственными магнитными моментами частиц.
Магнитное поле действует только на движущиеся заряды. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути.
Основными характеристиками магнитного поля являются магнитная индукция, напряженность и магнитный момент.
Индукция, напряжённость магнитного поля, магнитная проницаемость
Механическое действие, которое магнитное поле оказывает на другие тела, можно характеризовать вектором силы, а само поле – векторной физической величиной, называемой магнитной индукцией, которая позволяет определить эту силу. Магнитная индукция обозначается буквой  , измеряется в теслах (Тл).
, измеряется в теслах (Тл).
Индукция магнитного поля – векторная физическая величина, численно равная силе, действующей в однородном магнитном поле на проводник единичной длины с единичной силой тока, расположенный перпендикулярно магнитным силовым линиям.
Магнитная индукция  является основной силовой характеристикой магнитного поля. Индукция магнитного поля может быть определена в любой точке пространства и в любой момент времени:
является основной силовой характеристикой магнитного поля. Индукция магнитного поля может быть определена в любой точке пространства и в любой момент времени:
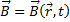 .
.
Направление вектора магнитной индукции задается направлением магнитной стрелки, помещенной в данную точку поля. Оно совпадает с направлением, которое указывает северный полюс стрелки (рис. 1).
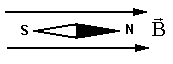 Рис.1. Рис.1. |
 и
и  , где
, где  – напряженность,
– напряженность,  – индукция магнитного поля.
– индукция магнитного поля. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим выражением:  , А/м,
, А/м,
где 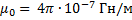 — магнитная постоянная,
— магнитная постоянная,  – безразмерная величина – магнитная проницаемость среды, которая показывает, во сколько раз индукция магнитного поля в среде
– безразмерная величина – магнитная проницаемость среды, которая показывает, во сколько раз индукция магнитного поля в среде  больше индукции
больше индукции 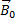 в вакууме (в вакууме
в вакууме (в вакууме  ):
):
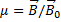
Магнитная проницаемость зависит от свойств среды, в которой создаётся магнитное поле[9].
Напряженность  не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводников на интенсивность магнитного поля в данной точке пространства. Однако, вектор
не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводников на интенсивность магнитного поля в данной точке пространства. Однако, вектор  является важной, но вспомогательной характеристикой магнитного поля. Основной характеристикой магнитного поля всё же является вектор
является важной, но вспомогательной характеристикой магнитного поля. Основной характеристикой магнитного поля всё же является вектор  .
.
Магнитный момент контура с током
Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром (рис. 2).
 Рис. 2. Рис. 2. |
 к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали
к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали  (рис. 2).
(рис. 2). Векторную величину 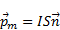
называют магнитным моментом контура, который в СИ измеряется в  , где
, где  - ток контуре,
- ток контуре,  - площадь контура с током.
- площадь контура с током.
1.2. Магнитное поле в веществе. Магнетики
Все вещества в большей или меньшей степени обладают магнитными свойствами.
Магнетик – МАГНЕТИК термин, применяемый ко всем веществам при рассмотрении их магнитных свойств.
Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками[10] и внутреннего, или собственного, магнитного поля, создаваемого микротоками[11].
Намагниченное вещество создает магнитное поле  , которое накладывается на внешнее поле
, которое накладывается на внешнее поле  0 (поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией
0 (поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией
 ,
,
причем под здесь  и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.
и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.
Разнообразие типов магнетиков обусловлено различием магнитных свойств микрочастиц, образующих вещество, а также характера взаимодействия между ними.
Для объяснения способности тел к намагничиванию, Ампер предположил, что в молекулах вещества циркулируют круговые токи (получившие впоследствии название молекулярных токов Ампера). Каждый такой ток обладает собственным магнитным моментом 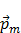 и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.3). Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается, а его суммарный магнитный момент становится отличным от нуля (см. рис.3).
и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.3). Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается, а его суммарный магнитный момент становится отличным от нуля (см. рис.3).
 Рис.3. Рис.3. |
Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым(spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.
Все вещества (и вообще среды) в отношении их магнитных свойств делятся на следующие основные группы:
· Антиферромагнетики – вещества, в которых установился антиферромагнитный порядок магнитных моментов атомов или ионов: магнитные моменты веществ направлены противоположно и равны по силе.
· Диамагнетики – вещества, намагничивающиеся против направления внешнего магнитного поля 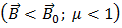 .
.
Молекулы диамагнетика собственного магнитного момента не имеют. Он возникает у них только под действием внешнего магнитного поля и направлен против него. Таким образом, результирующее магнитное поле в диамагнетике меньше, чем внешнее поле, правда, на очень малую величину. Это приводит к тому, что при перемещении диамагнетика в неоднородное магнитное поле он стремится сместиться в ту область, где напряженность магнитного поля меньше.
· Парамагнетики – вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля 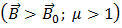 .
.
Молекулы (или атомы) парамагнетика имеют собственные магнитные моменты, которые под действием внешних полей ориентируются по полю и тем самым создают результирующее поле, превышающее внешнее. Парамагнетики втягиваются в магнитное поле. Так, например, жидкий кислород – парамагнетик, он притягивается к магниту.
· Ферромагнетики – вещества, в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов 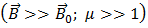 .
.
· Ферримагнетики – материалы, у которых магнитные моменты вещества направлены противоположно и не равны по силе.
К перечисленным выше группам веществ в основном относятся обычные твердые или (к некоторым) жидкие вещества, а также газы. Существенно отличается взаимодействие с магнитным полем сверхпроводников и плазмы.
1.3. Магнитный момент атома
Атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов. Движение электронов в атомах подчиняется квантовым законам. Магнетизм вещества удается объяснить посредством модели Бора, согласно которой электроны в атомах движутся по стационарным круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом:  , модуль которого равен:
, модуль которого равен:
 , (1)
, (1)
где 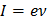 – сила кругового тока, вызванного движением электрона по орбите вокруг ядра атома;
– сила кругового тока, вызванного движением электрона по орбите вокруг ядра атома;  – частота вращения электрона по орбите;
– частота вращения электрона по орбите;  – площадь орбиты. Если электрон движется по часовой стрелке (рис. 4), то ток направлен против часовой стрелки и вектор
– площадь орбиты. Если электрон движется по часовой стрелке (рис. 4), то ток направлен против часовой стрелки и вектор  (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона.
(в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона.
 Рис. 4. Орбитальные магнитный момент Рис. 4. Орбитальные магнитный момент  и механический момент и механический момент  l электрона. l электрона. |
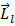 , модуль которого:
, модуль которого:  , (2)
, (2)
где  r – скорость движения электрона по орбите,
r – скорость движения электрона по орбите,  – площадь орбиты.
– площадь орбиты.
Вектор 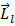 (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Из рис. 4 следует, что направление
(его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Из рис. 4 следует, что направление  и
и 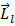 противоположны, поэтому, учитывая выражение (1) и (2), получим:
противоположны, поэтому, учитывая выражение (1) и (2), получим:
 , (3)
, (3)
где величина
 (4)
(4)
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком << – >>, указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения  и
и  различны. Формула (4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.
различны. Формула (4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.
Позже, в опытах Эйнштейна и де Гааза, выяснилось, что наряду с орбитальными моментами, электрон обладает также собственным механическим моментом (спином) 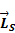 (т.е. подобен волчку)и собственным магнитным моментом
(т.е. подобен волчку)и собственным магнитным моментом  , для которых гиромагнитное отношение оказалось в два раза большим:
, для которых гиромагнитное отношение оказалось в два раза большим:
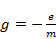 ,`
,` 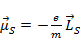
Магнитный момент атома слагается из орбитальных и собственных магнитных моментов входящих в его состав электронов, а также магнитного момента ядра атома. Магнитный момент ядра, обусловленный магнитными моментами входящих в состав ядра протонов и нейтронов, значительно меньше электронных магнитных моментов, поэтому при рассмотрении многих вопросов им можно пренебречь. Таким образом, полный магнитный момент атома равен векторной сумме магнитных моментов всех его электронов. Магнитный моментмолекулы также можно считать равным сумме магнитныхмоментов входящих в ее состав электронов.
1.4. Намагниченность
Различные вещества в той или иной степени способны к намагничиванию: то есть под действием магнитного поля, в которое их помещают, приобретать магнитный момент. Одни вещества намагничиваются сильнее, другие слабее.
Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность (вектор намагничивания)  .
.
Намагни́ченность – векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела; определяется как магнитный момент единицы объёма вещества:
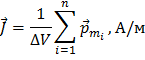
где  – магнитный момент
– магнитный момент  – го атома из числа
– го атома из числа 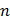 атомов, в объеме
атомов, в объеме  .
.
1.5. Диамагнетизм и парамагнетизм
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.
В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.
Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.
1.6. Ферромагнетизм
Ферромагнетиками называются твердые тела, которые могут обладать спонтанной намагниченностью, т. е. намагничены уже в отсутствии магнитного поля.
Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах  . Например, у стали
. Например, у стали 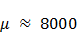 , у сплава железа с никелем магнитная проницаемость достигает значений 250000.
, у сплава железа с никелем магнитная проницаемость достигает значений 250000.
К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.
Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.
Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна  , у кобальта
, у кобальта  , у никеля
, у никеля 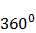 C.
C.
Ферромагнитные материалы делятся на две большие группы – на магнито-мягкиеи магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).
Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовления постоянных магнитов.
Магнитная проницаемость  ферромагнетиков не является постоянной величиной;она сильно зависит от индукции
ферромагнетиков не является постоянной величиной;она сильно зависит от индукции  внешнего поля. Типичная зависимость
внешнего поля. Типичная зависимость 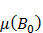 приведена на рис. 5. В таблицах обычно приводятся значения максимальной магнитной проницаемости.
приведена на рис. 5. В таблицах обычно приводятся значения максимальной магнитной проницаемости.
Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции  магнитного поля в ферромагнетике от индукции
магнитного поля в ферромагнетике от индукции  внешнего магнитного поля.
внешнего магнитного поля.
 Рис. 5. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля. Рис. 5. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля. |
Характерной особенностью процесса намагничивания ферромагнетиков является магнитный гистерезис[12], то есть зависимость намагничивания от предыстории образца.
 Рис. 6. Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции Рис. 6. Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции 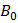 внешнего магнитного поля. внешнего магнитного поля. |
Кривая намагничивания
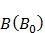 ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 6).
ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 6). Из рис. 6 видно, что при 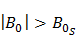 наступает магнитное насыщение – намагниченность образца достигает максимального значения. Если теперь уменьшать магнитную индукцию
наступает магнитное насыщение – намагниченность образца достигает максимального значения. Если теперь уменьшать магнитную индукцию  внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно
внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно 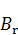 . Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию
. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию  до значения –
до значения – 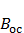 , которое принято называть коэрцитивной силой (коэрцитивное поле имеет направление, противоположное полю, вызвавшему намагничивание). Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 6.
, которое принято называть коэрцитивной силой (коэрцитивное поле имеет направление, противоположное полю, вызвавшему намагничивание). Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 6.
 Рис. 7. Рис. 7. |
Если довести намагниченность до насыщения и затем уменьшать напряженность магнитного поля, то намагниченность изменяется не по первоначальной кривой 0–1, а изменяется в соответствии с кривой 1–2. В результате, когда напряженность внешнего поля станет равной нулю, намагниченность не исчезает, а характеризуется величиной  , которая называется остаточной намагниченностью. Первоначальной намагниченности образец достигает под действием поля
, которая называется остаточной намагниченностью. Первоначальной намагниченности образец достигает под действием поля  , которое называется коэрцитивной силой.
, которое называется коэрцитивной силой.
У магнито-мягких материалов значения коэрцитивной силы 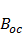 невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.
невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.
Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка  см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.
см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.
В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля  происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция
происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция
 Рис. 8. Рис. 8. |
Ферромагнетизм (англ. ferromagnetism) - магнитоупорядоченное состояние вещества, в котором большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью.
1.7. Магнитная восприимчивость
Вектор намагничивания 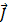 принято связывать не с магнитной индукцией
принято связывать не с магнитной индукцией 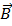 , а с напряженностью магнитного поля
, а с напряженностью магнитного поля 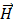 и, как показывает опыт, для диа– и парамагнетиков, вектор
и, как показывает опыт, для диа– и парамагнетиков, вектор  связан с вектором
связан с вектором 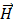 соотношением:
соотношением:
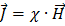 ,
,
где 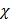 – характерная для данного магнетика величина, называемая магнитной восприимчивостью.
– характерная для данного магнетика величина, называемая магнитной восприимчивостью.
Поскольку  имеет ту же размерность, что и
имеет ту же размерность, что и 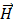 , [A/м], то
, [A/м], то 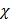 – безразмерная величина. На основании двух последних формул имеем:
– безразмерная величина. На основании двух последних формул имеем:
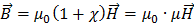
где 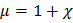 .
.
В то время как диэлектрическая проницаемость  у всех веществ всегда больше единицы (диэлектрическая восприимчивость
у всех веществ всегда больше единицы (диэлектрическая восприимчивость 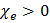 ), магнитная проницаемость
), магнитная проницаемость 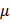 может быть как больше единицы, так и меньше единицы (соответственно магнитная восприимчивость
может быть как больше единицы, так и меньше единицы (соответственно магнитная восприимчивость 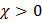 – у парамагнетиков и
– у парамагнетиков и 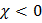 – у диамагнетиков; у ферромагнетиков –
– у диамагнетиков; у ферромагнетиков – 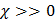 ).
).
1.8. Точка Кюри
Точка Кюри, или температура Кюри (Тс), – температура фазового перехода II рода, связанного со скачкообразным изменением свойств симметрии вещества (например, магнитной – в ферромагнетиках, электрической – в сегнетоэлектриках, кристаллохимической – в упорядоченных сплавах). Названа по имени П. Кюри.
В более узком смысле:точка Кюри - температура, выше которой исчезает самопроизвольная намагниченность доменов ферромагнетиков и ферромагнетик переходит в парамагнитное состояние.
При температуре 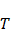 ниже точки Кюри
ниже точки Кюри 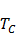 ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью и определённой магнитно-кристаллической симметрией. В точке Кюри
ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью и определённой магнитно-кристаллической симметрией. В точке Кюри 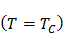 интенсивность теплового движения атомов ферромагнетика оказывается достаточной для разрушения доменов т.е. его самопроизвольной намагниченности(тепловое движение атомов «расшатывает» существующий магнитный порядок - одинаковую ориентацию магнитных моментов атомов) и в результате ферромагнетик становится парамагнетиком.
интенсивность теплового движения атомов ферромагнетика оказывается достаточной для разрушения доменов т.е. его самопроизвольной намагниченности(тепловое движение атомов «расшатывает» существующий магнитный порядок - одинаковую ориентацию магнитных моментов атомов) и в результате ферромагнетик становится парамагнетиком.
Аналогично у антиферромагнетиков при 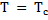 (в так называемой антиферромагнитной точке Кюри или точке Нееля) происходит разрушение характерной для них магнитной структуры (магнитных подрешёток), и антиферромагнетики становятся парамагнетиками.
(в так называемой антиферромагнитной точке Кюри или точке Нееля) происходит разрушение характерной для них магнитной структуры (магнитных подрешёток), и антиферромагнетики становятся парамагнетиками.
Численные значения температуры Кюри приводятся в специальных справочниках.
При охлаждении ферромагнетика ниже температуры Кюри 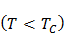 его ферромагнитные свойства восстанавливаются.
его ферромагнитные свойства восстанавливаются.
Закон Кюри – Вейса
Закон Кюри – Вейса описывает магнитную восприимчивость ферромагнетика в области температур выше точки Кюри (то есть в парамагнитной области). Закон выражается следующей математической формулой:
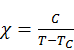 ,
,
где  – магнитная восприимчивость,
– магнитная восприимчивость,
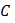 – постоянная Кюри, зависящая от вещества,
– постоянная Кюри, зависящая от вещества,
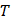 – абсолютная температура в кельвинах,
– абсолютная температура в кельвинах,
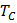 – температура Кюри, К.
– температура Кюри, К.
При 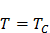 магнитная восприимчивость стремится к бесконечности. При снижении температуры до точки Кюри и ниже возникает спонтанная намагниченность вещества.
магнитная восприимчивость стремится к бесконечности. При снижении температуры до точки Кюри и ниже возникает спонтанная намагниченность вещества.
