Электронная теория Лоренца. Простой эффект Зеемана

В случае простого эффекта Зеемана число компонент расщепления, смещение частот спектральных линий и характер поляризации излучения достаточно полно объясняются с помощью классической электронной теории Лоренца. В теории излучение монохроматического света рассматривается как результат движения электрона по простому гармоническому закону, т. е. под действием квазиупругой силы, а изменение излучения под действием магнитного поля ⎯ как следствие изменения характера движения электрона из-за появления добавочной силы магнитного воздействия на движущийся электрон.

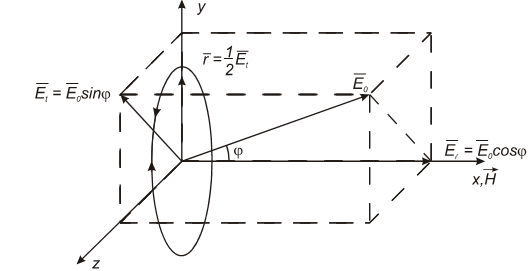
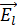Рассмотрение простого эффекта Зеемана в классической электродинамике основывается на разложении орбитального движения электрона на два линейных гармонических колебания по двум взаимно перпендикулярным направлениям, т. е. со сдвигам фаз на , частотой ν₀ и амплитудой E₀ (рис. 2.1), из которых первое колебание совершается вдоль налагаемого внешнего магнитного поля 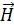, а другое 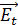⎯ перпендикулярно полю 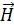. В свою очередь, компоненту 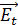можно рассматривать как результат двух равномерных и противоположно направленных круговых движений с одинаковым радиусом 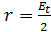и частотой ν₀ в плоскости, перпендикулярной направлению индукции магнитного поля .

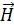При наложении внешнего магнитного поля на движущийся электрон действует добавочная сила Лоренца, равная:

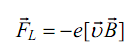
(3.1)

где е — заряд электрона, 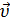скорость его движения; 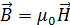- магнитная индукция. Действие магнитного поля на продольную компоненту 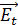отсутствует, поэтому гармоническое колебание вдоль поля остается неизменным и сохраняет первоначальную частоту ν₀. Действие же магнитного поля 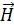на круговое движение в плоскости, перпендикулярной 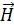, будет приводить при постоянном радиусе орбиты к изменению скорости вращения электрона.

Условие механической устойчивости атома в отсутствие внешнего

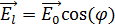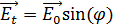Рис.3.1.

Разложение линейного движения на два кругополяризованных вращения спротивоположными фазами магнитного поля примет вид:

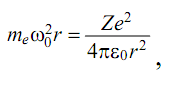
(3.2)

где ω₀ - круговая частота электрона в отсутствие магнитного поля.

При наложении магнитного поля центростремительная сила для круговых движений изменится вследствие добавления силы Лоренца, и условия механической устойчивости атома соответственно для правого и левого круга примут вид:

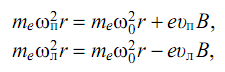
(3.3)

где ω_п и ω_л — круговые частоты электрона для правого и левого

круговых движений при наложении магнитного поля.

Линейные скорости движения электрона соответственно:

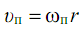
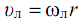
поэтому уравнения (3.3) запишем как:

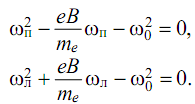
(3.4)

Их решения имеют вид:

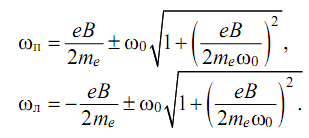
(3.5)

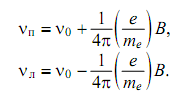
(3.6)

Из электродинамики известно, что движущийся по орбите электрон в атоме можно рассматривать как диполь — гармонический осциллятор. Такой диполь, осциллирующий с определенной частотой, представляет собой источник монохроматического излучения той же частоты. Если в отсутствие магнитного поля спектральный аппарат независимо от направления наблюдения в спектрах испускания или поглощения обнаруживает несмещенную неполяризованную спектральную линию частоты ν₀ , то при наложении магнитного поля движение становится сложным. Соответственно будет сложным и спектр излучения электрона: его можно представить как совокупность трех монохроматических волн различной частоты — (ν₀ −Δν ), ν₀, ν₀+Δν в различных состояниях поляризации. Внешнее магнитное поле изменяет характер поляризации излучения.

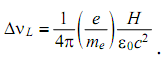
(3.7)

С учетом связи 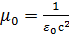, выражения (2.4 )для магнетона Бора и связи напряженности магнитного поля H с индукцией B в вакууме 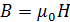, перепишем уравнение (3.7) в следующем виде:

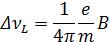
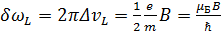(3.8)

Так как 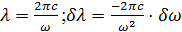, то в шкале длин волн величина расщепления спектральных линий в магнитном поле выражается формулами:

(3.9)

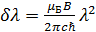
Компонента магнитного расщепления с направлением колебаний электрического вектора 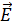вдоль направления силовых линий магнитного поля 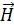называется π (параллельной)-компонентой, а компоненты с направлением колебаний 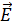, перпендикулярным магнитному полю 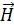- σ (перпендикулярной)-компонентами. По интенсивности π-компонента примерно в 2 раза сильнее, чем каждая из σ-компонент.

Объясняемый электронной теорией Лоренца простой эффект Зеемана наблюдается лишь для одиночных, или «синглетных», спектральных линий.

Магнитное расщепление большинства отдельных спектральных линий мультиплетов (дублетов, триплетов и т.д.) в слабых магнитных полях имеет сложный характер. Наблюдаемый эффект в этом случае называется сложным (аномальным) эффектом Зеемана.

При этом в сильных магнитных полях сложное расщепление упрощается и отмечается простое расщепление Зеемана (так называемый эффект Пашена-Бака).