Теоретические основы работы

ЦЕЛЬ РАБОТЫ

Экспериментальное определение коэффициентов внутрен-него трения и диффузии воздуха, длины свободного пробе-га и эффективного диаметра молекул воздуха.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

В настоящей работе исследуются процессы, с помощью ко-торых происходит установление состояния теплового равно-весия. Такие процессы носят название кинетических. Все эти процессы, приближающие тело к состоянию равнове-сия, являются необратимыми. К кинетическим явлениям, или явлениям переноса, относятся диффузия, теплопровод-ность и вязкость. Во всех трех случаях осуществляется мо-лекулярный перенос некоторой величины из одной части тела в другую и тем самым происходит приближение к сос-тоянию теплового равновесия. В работе исследуются два явления переноса: внутреннее трение (вязкость) и диф-фузия в газах.

Внутреннее трение – это свойство газа оказывать сопро-тивление перемещению одного слоя вещества относительно другого. При движении плоских слоев газа сила трения между слоями описывается законом Ньютона (2.11).

Рассмотрим ламинарное течение газа, т.е. случай, когда слои газа движутся параллельно друг другу, но с различной скоростью. Тепловое движение молекул, переходящих из одного слоя в другой и сталкивающихся друг с другом, приводит к переносу импульса от быстрых слоев к мед-ленным. Вследствие этого скорости слоев выравниваются, а их взаимодействие можно описывать при помощи силы тре-ния (2.11).

При движении газа по трубе из-за межмолекулярного взаимодействия газа и стенок трубы возникает различие в скорости движения разных слоев газа. Обычно считают, что газ «прилипает» к стенкам и скорость потока на ней можно положить равной нулю. Таким образом, скорость потока га-за заметно меняется в некоторой области около стенок труб-ки. Эта область носит название пограничного слоя.

Если ширина пограничного слоя много меньше размеров поперечного сечения потока, то он не оказывает сколько-нибудь заметного влияния на течение газа. Однако если диаметр трубы сравним с шириной пограничного слоя, то влиянием вязкости уже пренебречь нельзя. Именно так об-стоит дело в узких трубках, или капиллярах.

Рассмотрим течение газа через трубку радиуса 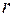и длины 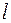под действием разности давлений 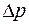на концах трубки. Направим ось 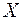от оси трубки к ее стенке. В установив-шемся режиме зависимость скорости газа от расстояния 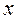до оси трубки описывается параболическим законом:

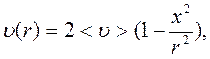(2.5.1)

где 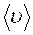– средняя по сечению скорость.

Получим на основе выражения (2.5.1) и закона Ньютона (2.11) расчетную формулу определения коэффициента вяз-кости.

Вычислим значение производной 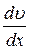на стенке трубки, т.е. при :

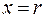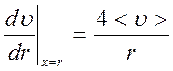. (2.5.2)

Подставляя это выражение в формулу Ньютона (2.11), получаем выражение для силы трения газа о стенки трубки

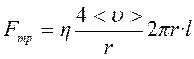. (2.5.3)

где 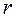– радиус трубки,

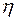– вязкость газа.

В установившемся режиме сила трения 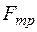уравнове-шивает внешнюю силу

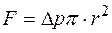, (2.5.4)

действующую на газ в трубке и создающую ток газа.

Объединяя (2.5.3) и (2.5.4), получаем выражение для средней по сечению скорости потока газа:

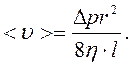(2.5.5)

Непосредственное измерение средней скорости газа 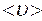связано с большими трудностями, поэтому измеряют про-порциональную ей величину – расход газа, т.е. объем газа 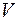, протекающего за 1 секунду через капилляр:

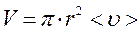(2.5.6)

Таким образом, для расхода газа 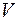получаем выражение:

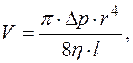(2.5.7)

которое называется формулой Пуазейля. В настоящей рабо-те эта формула является расчетной для определения коэф-фициента вязкости воздуха:

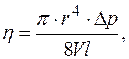(2.5.8)

где 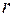– радиус трубки;

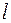– ее длина;

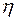– вязкость газа.

Выясним условия, при которых применима формула Пуа-зейля.

Прежде всего, необходимо, чтобы течение газа было ла-минарным. Характер движения газа в трубке определяется безразмерной комбинацией параметров, которая называется числом Рейнольдса:

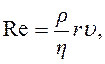(2.5.9)

где 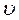– скорость потока,

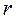– радиус трубки;

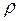– плотность газа;

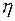– его вязкость.

В гладких трубках круглого сечения переход от ламинар-ного течения к турбулентному происходит при 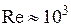, сле-довательно, необходимо, чтобы с достаточным запасом вы-полнялось неравенство:

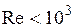. (2.5.10)

Необходимо также, чтобы при течении сквозь капилляр не происходило существенного изменения удельного объе-ма газа, т.е. перепад давлений вдоль трубки был малым по сравнению с самим давлением.

Характерное для ламинарного течения параболическое распределение скоростей (2.5.1) устанавливается не сразу, а на некотором расстоянии 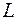от входа в трубку:

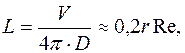(2.5.11)

где 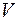– расход газа,

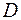– коэффициент диффузии.

Диффузия – это самопроизвольное перемешивание моле-кул, происходящее вследствие их теплового движения. Обычно диффузия связывается с изменением концентрации в пространстве и возникновением диффузного потока ве-щества в направлении уменьшения концентрации. Процесс происходит до тех пор, пока равновесие не будет восста-новлено и концентрация не станет одинаковой по всему объему.

Назовем диффузионным потоком 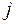число молекул ве-щества, проходящего в 1 секунду через единичную площад-ку, перпендикулярную оси 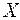. Из опыта известно, что ста-ционарный диффузионный поток пропорционален градиен-ту концентрации, взятому с обратным знаком. На основе уравнения (2.5) получаем выражение, описывающее диффу-зионный поток в газе:

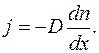(2.5.12)

Здесь 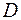– постоянный коэффициент, называемый коэф-фициентом диффузии (2.6). В данной работе коэффициент диффузии определяется, согласно соотношению (2.12), из коэффициента внутреннего трения:

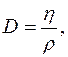(2.5.13)

где 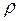- плотность воздуха при давлении и температуре в мо-мент проведения эксперимента. Плотность определяется по таблице в Приложении 3.

Коэффициент диффузии позволяет нам определить нес-колько важных молекулярно-кинетических характеристик газа: среднюю длину свободного пробега 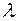и эффективный диаметр 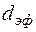молекул газа.

Средней длиной свободного пробега 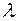называется путь, проходимый молекулой между двумя последовательными столкновениями.

Если считать молекулы газа подобными твердыми шари-ками, то размеры молекулы можно определить как рассто-яние между их центрами при столкновении. Это расстояние называют эффективным диаметром молекулы .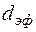

Найдем выражение для вычисления средней длины сво-бодного пробега 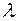. Из уравнения (2.6) получаем:

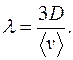(2.5.14)

Здесь 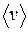– средняя арифметическая скорость теплового движения молекул:

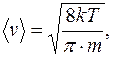(2.5.15)

где 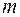– масса молекулы,

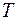– температура газа,

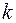– постоянная Больцмана.

Выражение (2.4.15) можно привести к более удобному для использования виду:

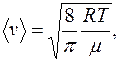(2.5.16)

где 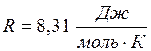– универсальная газовая постоянная,

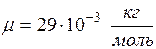– молярная масса воздуха.

Тогда

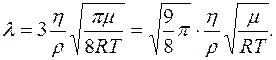(2.5.17)

Плотность воздуха 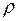для произвольных условий опре-деляется исходя из уравнения Менделеева–Клапейрона :

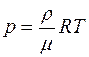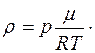(2.5.18)

Подставив уравнение для плотности (2.5.18) в (2.5.17), получаем:

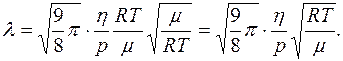
Окончательно,

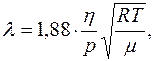(2.5.18)

где 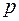– атмосферное давление.

Для нахождения эффективного диаметра молекул вос-пользуемся следующим выражением:

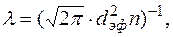(2.5.19)

где 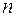– число молекул в единичном объеме. Его можно оп-ределить при помощи числа Лошмидта 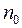, т.е. числа моле-кул идеального газа в кубическом сантиметре при нор-мальных условиях:

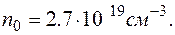(2.5.20)

Для произвольных условий:

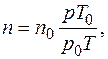(2.5.21)

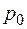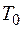где и – давление и температура при нормальных усло-виях ( 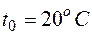и 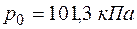). Для расчета эффективного диаметра молекул получаем следующее уравнение:

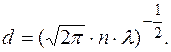(2.5.22)

Для расчетов необходимо знать геометрические размеры капиллярной трубки, разность давлений на ее концах, рас-ход газа, а также атмосферное давление и температуру.

ОПИСАНИЕ УСТАНОВКИ И ЭКСПЕРИМЕНТАЛЬНОГО МЕТОДА

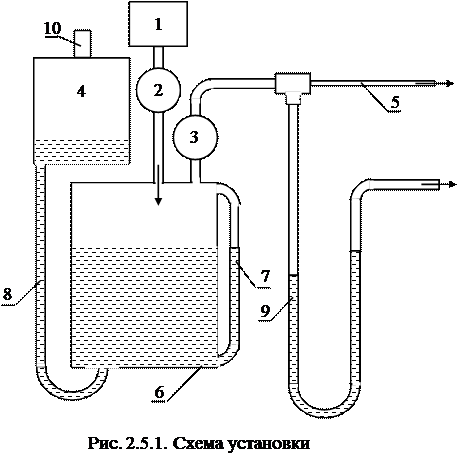
Схема экспериментальной установки приведена на рис. 2.5.1. Капилляр 5 одним концом соединен с мерной емкостью 6. Другой конец капилляра сообщается с атмосферой. Мерная емкость 6 соединена резиновой трубкой 8 со вспомога-тельным сосудом с водой 4. При включении воздушного компрессора 1 и нажатии клапана 2 вода вытесняется из мерной емкости во вспомогательный сосуд, при этом в мер-ной емкости устанавливается избыточное по сравнению с атмосферным давление. Затем клапан 2 следует отпустить (закрыть). Находившийся во вспомогательном сосуде воз-дух легко вытесняется водой через трубку большого сече-ния 10. При нажатии на клапан 3 (его открывании) начи-нается течение воздуха через капилляр под действием раз-ности давлений на его концах.

Разность давлений на концах капилляра можно измерить с помощью манометра 9, она равна:

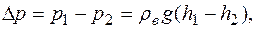(2.5.23)

где 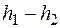– разность уровней воды в манометре;

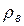– плотность воды;

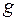– ускорение свободного падения.

Объем поступающего в мерную емкость воздуха опреде-ляют по измерению уровня воды в этой емкости.