Вращательное движение твёрдых тел

· Момент инерции материальной точки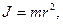

где m — масса точки; r— расстояние до оси вращения.

· Моменты инерции тел правильной геометрической формы (тела считаются однородными; m — масса тела) представлены в таблице:

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр или кольцо радиусом R	Ось симметрии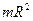
Сплошной цилиндр или диск радиусом R	Ось симметрии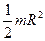
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину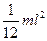
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец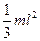
Шар радиусом R	Ось проходит через центр шара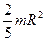

· Теорема Штейнера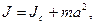

где 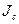- момент инерции тела относительно оси, прохо­дящей через центр масс; J - момент инерции относи­тельно параллельной оси, отстоящей от первой на рас­стоянии а; m - масса тела.

Пример: Найти момент инерции шара относительно оси 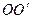, находящейся на расстоянии 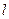от поверхности шара (рис.4).

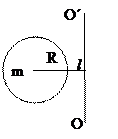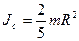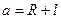Здесь ; . Следовательно

.

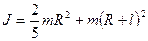Рис.4

· Кинетическая энергия тела, вращающегося вокруг неподвижной оси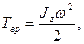

где 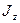- момент инерции тела относительно оси z; 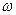- его угловая скорость.

· Кинетическая энергия тела, катящегося по плоскости без скольжения,

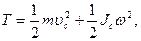
где m - масса тела; 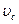- скорость центра масс тела; 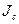- момент инерции тела относительно оси, проходя­щей через его центр масс; 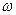- угловая скорость тела.

· Момент силы относительно неподвижной точки

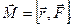
где 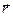- радиус-вектор, проведенный из этой точки в точ­ку приложения силы 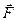. Модуль момента силы относительно неподвижной оси

,

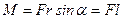где 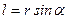- плечо силы (кратчайшее расстояние между ли­нией действия силы и осью вращения), 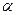- угол между направлениями силы и радиус-вектора. Направление момента силы совпадает с осью, относительно которой происходит вращение, и может быть определено по правилу буравчика.

· Работа тела при вращательном движении

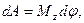
где 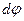- угол поворота тела; 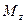- момент силы относи­тельно оси z.

· Момент импульса (момент количества движения) твердого тела (Рис.5) относительно оси вращения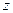

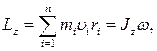
где 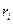- расстояние от оси z до отдельной частицы тела; 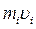- импульс этой частицы; 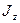- момент инерции те­ла относительно оси z; 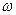- его угловая скорость.

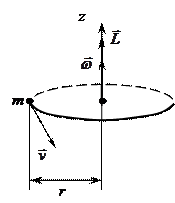
Рис.5

· Уравнение (закон) динамики вращательного дви­жения твердого тела относительно неподвижной оси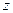

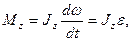
где 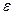- угловое ускорение; 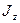- момент инерции тела относительно оси z.

· Закон сохранения момента импульса для замкнутой системы тел

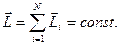
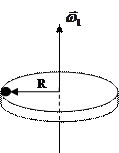
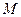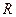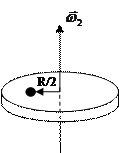
Пример: Платформа в форме диска массой и радиусом вращается относительно вертикальной оси, проходящей через ось симметрии. На краю платформы стоит человек массой 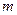(рис.6,а). Как изменится угловая скорость вращения, если человек перейдёт на расстояние 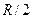ближе к оси (рис.6,б) (человека считать материальной точкой)?

а) б)

Рис.6

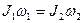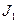По закону сохранения момента импульса , где и 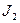- моменты инерции платформы с человеком в первом и втором случаях, т.е.

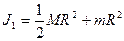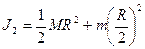; . Получаем:

.
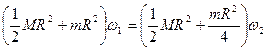
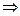
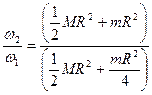